Дискурсивные, табличные, графические и формальные модели

Если за основание взять уже не смысловое содержание, а характер знаковой формы выражения, то получаем иную классификацию.

Дискурсивные модели - любые концепции и теории, представ­ленные в естественном языке (русском, английском и т. д.). Они мо­гут иметь описательный, эвристический или объяснительный статус (см. выше). Эвристические и объяснительные дискурсивные модели часто дополняются графическими моделями (диаграммами, графи­ками, графами), реже - формулами.

Все предметные, системные и математические модели имеют дискурсивную составляющую. Современные математические моде­ли, как правило, имеют формализованные компоненты (например, системы уравнений, записанные буквенными формулами).

Табличные модели (таблицы) - наиболее удобный и компакт­ный способ представления множественных эмпирических данных. В компьютерной обработке данных могут использоваться сложные многомерные структуры данных, где в ячейки вложены свои табли­цы и т. д. Однако для «ручного» использования наиболее удобными, наглядными являются обычные двумерные таблицы «строка -столбец - ячейка». Такие таблицы являются удобным промежуточ­ным звеном между дискурсивными фактологическими суждениями (например, «значение строки 1 по столбцу А в ячейке А1 таково») и графиками, которые наглядно представляют структуру данных.

Графические модели - это всевозможные схемы, диаграммы, карты, рисунки, прорисовки и т. п., служащие для наглядного цело­стного представления о предмете, его частях, сторонах, аспектах. Главные типы графических моделей (временные графики, пара­метрические пространства, модели фазовых переходов и тренд-структуры), а также взаимосвязи между ними будут рассмотрены ниже.

Формальные модели - специально сконструированные выраже­ния, как правило, состоящие из букв и цифр, логических, алгебраи­ческих и подобных знаков (алгебраические, логические или иные формулы, системы уравнений и т. п.), допускающие преобразования по фиксированным правилам без обращения к смысловым значени-

Глава 18. Основы методологии

ям, приписанным отдельным знакам. Наиболее распространенными являются дифференциальные системы уравнений в математических моделях исторической динамики (Турчин 2007). При отсутствии требуемых массивов числовых данных (что обычно за пределами исторической демографии и экономической истории) важнейшим типом формальных моделей, вероятно, является аппарат булевой алгебры в версии Ч. Рэгина.

Типы графических моделей

Временные графики, выражающие динамические ряды, составляют­ся на основе эмпирических данных (предварительно заполненных таблиц) либо конструируются в качестве эвристических моделей, объяснительных гипотез. Графики - универсальное средство анали­за всевозможных трендов, волн и циклов, центрированного не на дискурсивном описании и объяснении, а на исследовании историче­ски изменчивых количественных параметров. Выявленные паттер­ны составляют обычно лишь феноменологию долговременных про­цессов, требующую теоретического анализа порождающих условий и механизмов. При совмещении с математической моделью, ап­проксимирующей график, последний можно экстраполировать на будущее. Построение временных графиков следует считать началь­ным этапом создания объяснительных моделей.

Параметрическое пространство - это искусственный теорети­ческий конструкт, образованный сочетанием шкалированных ка­честв (свойств, черт, характеристик, параметров) изучаемой цело­стности. Работа с параметрическими пространствами зиждется на общедоступных интуитивных основаниях, фиксированных как в обыденном, так и в научном языке. Каждый раз, когда мы гово­рим, что страна (общество, культура, цивилизация, человечество) «движется» в каком-либо направлении - к прогрессу, гибели, гло­бальному миру, демократии, процветанию, упадку и т. п. - мы уже, осознанно или нет, используем соответствующее простейшее (од-номерное - вырожденное) параметрическое пространство, в кото­ром то или иное «направление» означает полюс, к которому на­правлен вектор «движения», то есть социального изменения. Наи­более удобным, наглядным и весьма популярным является пред­ставление исторической динамики в двумерных параметрических пространствах.

Возьмем в качестве примера траектории развития нововремен­ных государств по Ч. Тилли (рис. 1).

Теория и методология истории

Высокая

-Россия

Португалия Арагон

Польша

Концентрация

Средств

Принуждения

 

Кастилия

Скандинавия

Итальянск города-государства

Голландия

 

Низкая

Концентрация капитала

-► Высокая

Рис. 1. Гипотетические траектории различных государств в XVI– XVII вв. (Тилли 2009)

Здесь у Тилли не было ни надежных эмпирических данных, ни, тем более, проверенной теории, из которой можно было бы вывес­ти данные траектории. Была построена эвристическая модель, от­ражающая предположение о том, что в развитых успешных госу­дарствах высока концентрация как капитала, так и средств прину­ждения, соответственно разные государства должны были идти «к единой цели», хоть и разными путями (см. также главу 7 на­стоящего издания). Далее Тилли примерно, «на глазок» представил предполагаемые траектории на основе своего неявного обобщения исторических описаний – где, в каком масштабе, раньше или позже были сконцентрированы средства принуждения (армии), а где – ка­питал (богатства, пригодные к инвестированию).

Верно, что такого рода модельные траектории имеют «всего лишь» гипотетический статус. Более того, часто авторы их не про­веряют, а во многих случаях такие гипотезы и невозможно прове­рить. При этом модели такого рода отнюдь не бесполезны, они крайне важны для общего осмысления темы, для удобного и на­глядного сообщения идей, а также для формулирования таких по­ложений, которые уже можно проверить.

Модель становится мощным исследовательским инструментом, если параметры, задающие такое пространство, прошкалированы,

Глава 18. Основы методологии

то есть имеют ту или иную структуру упорядоченных значе-ний (градаций, уровней, ступеней и т. д.), грубо говоря, линейку (о шкалах и шкалировании см. главу 20 настоящего издания).

Весьма продуктивным является заимствованное из синергетики И. Пригожина понятие аттрактора, особенно в противопоставле­нии зонам неустойчивости. Аттракторы могут определяться мате­матически при наличии соответствующих моделей и аппарата, но первостепенное значение имеет их концептуальное содержание. В этом плане под аттрактором понимается такая область парамет­рического пространства (то есть область значений одного, двух или более параметров системы), «попав» в которую, система склонна достаточно долго воспроизводиться без существенных изменений в историческом времени, пока накопление дисбалансов, дисфункций не «вытолкнет» социальную систему из этой зоны.

Окрестные состояния вокруг аттрактора имеют отчетливую тенденцию к приближению к нему. Состояние бифуркации (зона таких состояний) в данном случае понимается как нахождение сис­темы между двумя или более аттракторами, когда незначительное воздействие («случайное стечение исторических обстоятельств») может привести к неудержимому движению системы в сторону од­ного или другого аттрактора.

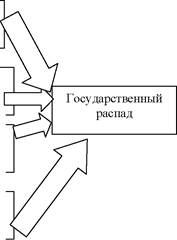
Модели фазовых переходов (см. выше) обычно изображаются графически как диаграммы с блоками, соединенными стрелками. Блоки обозначают фазы – периоды относительно стабильного со­стояния, а стрелки – переходы между ними во времени. Например, в виде фазовой модели (рис. 2) Р. Коллинз представил классиче­скую концепцию социальной революции и государственного рас­пада Теды Скочпол (см. главу 7 настоящего издания).

Теория и методология истории

 

Геополитическое напряжение

Внутриэлитный конфликт

ft

35.

Рост фискальной нагрузки

Военное поражение

Фискальное напряжение

Народное восстание

Рис. 2. Фазовая модель динамики государственного распада по Т. Скочпол (Коллинз 1998 а: 247; Skocpol 1979). Здесь четы­ре вертикально расположенных блока могут трактоваться либо как параллельные фазы, либо как составляющие од­ной большой фазы

С помощью фазовых моделей также удобно представлять би­фуркации (рис. 3), когда при разных условиях за одной фазой (так­ты 2 и 5) могут следовать разные другие фазы. Некоторые модели фазовых переходов могут быть замкнутыми, что обычно объясняет циклическую динамику. Ниже будет показано, как фазовые модели сочетаются с параметрическими.

Тренд-граф – стандартный способ представления факторных моделей (тренд-структур) в виде ориентированного графа, верши­нами которого являются факторы (шкалированные переменные, то есть свойства некоторой социальной целостности, способные ока­зывать воздействие на другие свойства), а ребрами-стрелками – причинные связи между ними, как линейные (усиление, ослабле­ние), так и нелинейные. В более точных математических моделях сама сила связи между переменными считается константой (или тоже переменной), тогда соответствующие стрелки обозначаются на тренд-графах буквами.

Глава 18. Основы методологии

 

Такт 4. Провал либеральных реформ

Распад государства

при отчуждении влиятельных групп и широких слоев населения

Такт 3. Попытка либеральных реформ

Такт 5.

при победе фракции реакционеров

Авторитарный

откат

^

при поддержке влиятельных групп, широких слоев населения и достаточности ресурсов

при победе фракции реформаторов

Такт 2. Стагнация: разложе­ние и приватизация государ­ства приводят к кризисам и конфликтам

Такт 1. Успешная авторитарная мобилизация

Рис. 3. Фазовая модель циклов социально-политической истории России. Темными стрелками обозначены альтернативные переходы, «выбор» которых зависит от обстоятельств (обозначенных курсивом)

Таким образом, тренд-структура (факторная модель) является понятийным содержанием тренд-графа (примерно так же, как на­учное понятие является содержанием слова-термина).

Тренд-графы в литературе называются по-разному: концепту­альные схемы, каузальные диаграммы, графы сложных причинных структур, структурно-динамические модели и т. д.

Довольно часто смешиваются фазовые переходы и тренд-структуры (в обоих случаях есть вершины-блоки и соединяющие их стрелки). Во избежание этого используется простой конвенци-альный прием: воздействия фактора на фактор в тренд-графах изо­бражаются одиночными стрелками, а переходы между фазами обо­значаются двойными стрелками. Это особенно важно, если в одной работе перемежаются тренд-структуры с фазовыми моделями.

В качестве примера приведем тренд-структуру и канонический граф функциональной причинности, детально исследованные Ар­туром Стинчкомбом (Stinchcombe 1987: 136; Розов 2001 б: 148– 164). Суть модели состоит в следующем (рис. 4). Некая структура, или повторяющая деятельность S (например, социальный институт, практика, ритуал или традиция), выбирается и используется сооб­ществом, что поддерживает на приемлемом уровне гомеостатиче-

Теория и методология истории

скую переменную H (например, безопасность, порядок, достаточ­ность ресурсов, лояльность, солидарность и т. д.), испытывающую разрушительные внешние или внутренние воздействия (напряже­ние, tension) T.

C – величина издер­жек от действия структуры

S – интенсивность действия обеспечивающей структуры

 

+

H– гомеостатическая переменная (параметр, жизненно важный для системы)

T – напряжение, угнетающее H

Рис. 4. Тренд-структура функциональной причинности

Действие структуры S тем интенсивнее, чем ниже значения гомео-статической переменной H (негативная связь). Сама же структура S своим действием восстанавливает, усиливает H (положительная связь), тем самым нейтрализуя угнетающее действие напряжения T.

Само действие структуры S «не бесплатно» и сопровождается издержками C (costs), которые растут по мере роста интенсивности S (положительная связь), причем рост издержек С естественным образом угнетает интенсивность структуры S (негативная связь).

Модель допускает множественные направления усложнения и развертывания: приписывание коэффициентов связям, умноже-ние переменных, особенно альтернативных обеспечивающих струк-тур и т. д. Здесь рассмотрим только принципиальные вопросы воз­можного использования функциональной тренд-структуры в ана­лизе исторической динамики и социальной эволюции.

По сути дела, данная модель покрывает все эмпирическое поле структурного функционализма (Б. Малиновский, Р. Мертон, Т. Пар-сонс и проч.; см. главу 22 настоящего издания). Функционализм часто (и отчасти справедливо) обвиняли в неспособности объяс­нять исторические, эволюционные изменения, само происхождение

Глава 18. Основы методологии

и смену функциональных структур, институтов и проч. Представ­ленная выше тренд-структура оказывается весьма гибким инстру­ментом, позволяющим работать именно с такими принципиальны­ми сдвигами. Могут появляться новые напряжения T₁, T₂..., новые параметры социальной системы становятся жизненно важными и требующими защиты: H₁, H₂... Главное же содержание социальной эволюции – появление новых социальных структур, форм деятель­ности и взаимодействия, социальных институтов S₁, S₂, … (дружин и армий, государств, служб сбора дани и налогов, полиции, произ­водственных организаций, рынков и бирж, церквей, школ, универ­ситетов и т. д.). Каждая такая структура поддерживает некие го-меостатические переменные H и каждая имеет свои издержки С. В переломные моменты истории происходит широкомасштабный переход от старых обеспечивающих структур к новым, обычно бо­лее эффективным (но не всегда и отнюдь не по всем аспектам).

Пример связи между моделями: тренд-структуры и системы уравнений

Заметим, что каждая тренд-структура вполне подвластна математи­зации (как правило, через переход к линейным или дифференци­альным уравнениям). Действительно, изменение каждой перемен­ной (вершины графа) складывается из изменений приходящих пе­ременных (других вершин, от которых идут стрелки-притоки). Рас­смотрим в качестве примера модель геополитической динамики Р. Коллинза (рис. 5, см. также главу 8 настоящего издания).

Для пяти переменных строится система из пяти дифференци­альных уравнений:

dT/dt = aW,

dR/dt = bT,

dW/dt = cR + eL + gM,

dL/dt = kT,

dM/dt = fT.

Следует отметить, что дифференциальные уравнения более вы­соких порядков не могут быть выражены средствами стандартных тренд-графов. Кроме того, сложные переключения контуров поло­жительной и отрицательной обратной связи вполне могут задавать­ся одной компактной системой дифференциальных уравнений. Та­ким образом, математический аппарат, как и следовало ожидать, выигрывает в емкости и строгости. Более детально о математиче­ском моделировании исторических процессов см. главу 23.

Теория и методология истории

Военный успех W

Геополитические ресур­сы (население и его богатство) R/-—\ О

Окраинность (доля безопасных границ) M

b

Величина контролируемой территории T

 

Рис. 5. Тренд-структура, выражающая теорию геополитической ди­намики Р. Коллинза