У дещо іншій формі проблему прогнозування можна сформулювати так: у разі одержання нової пари спостережень 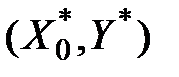 необхідно з'ясувати, чи задовольняє вона попередню залежність, тобто чи дорівнює
необхідно з'ясувати, чи задовольняє вона попередню залежність, тобто чи дорівнює 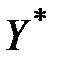 значенню
значенню 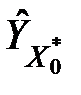 , отриманому підстановкою
, отриманому підстановкою 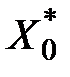 в рівняння моделі.
в рівняння моделі.
Алгоритм розв’язування оберненої задачі
Крок 1. Розглянемо величину 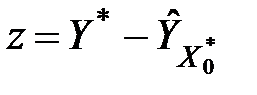 . Сформулюємо дві гіпотези:
. Сформулюємо дві гіпотези:
· H0 : 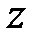 = 0, тобто значення
= 0, тобто значення 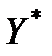 та
та 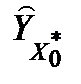 збігаються;
збігаються;
· H1 : 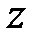 ≠ 0, значення
≠ 0, значення 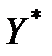 та
та 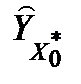 не збігаються.
не збігаються.
Крок 2. Величина 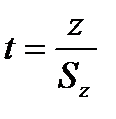 має розподіл Стьюдента з
має розподіл Стьюдента з 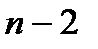 степенями вільності. Оцінку дисперсії величини z обчислимо за формулою
степенями вільності. Оцінку дисперсії величини z обчислимо за формулою
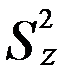 =
= 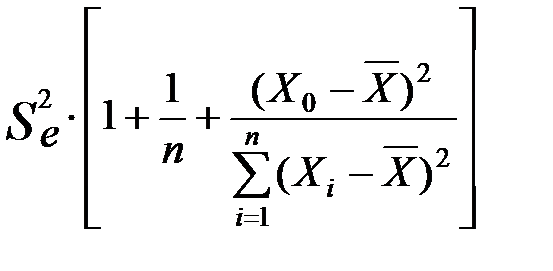 .
.
Крок 3. Застосуємо правило прийняття рішень:
· якщо розрахункове значення t-статистики менше табличного за модулем, то нульову гіпотезу слід прийняти, тобто з вибраним рівнем довіри можна стверджувати, що значення 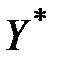 не відрізняється від значення
не відрізняється від значення 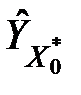 , знайденого за рівнянням моделі, і пара
, знайденого за рівнянням моделі, і пара 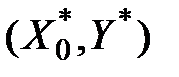 відповідає даній залежності;
відповідає даній залежності;
· якщо розрахункове значення t-статистики більше табличного, то нульову гіпотезу треба відкинути, тобто з вибраним рівнем довіри можна стверджувати, що значення 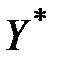 статистично значущо відрізняється від значення
статистично значущо відрізняється від значення 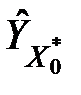 , знайденого за рівнянням моделі, і пара
, знайденого за рівнянням моделі, і пара 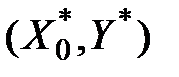 не відповідає даній залежності.
не відповідає даній залежності.
Приклад виконання розрахунків
Маємо статистичні дані про приріст прибутку (Y) за 7 підприємствами галузі залежно від інвестиційних вкладень в оборотні кошти (X1) і основний капітал (X2). Проаналізувати залежність приросту прибутку від цих показників, використовуючи початкові дані табл. 9.
Таблиця 9
| Y
| 50
| 120
| 290
| 190
| 200
| 300
| 320
|
| X1
| 30
| 66
| 78
| 110
| 130
| 190
| 250
|
| X2
| 6
| 10
| 20
| 15
| 16
| 18
| 20
|
Етапи розв’язування
І. Побудова моделі
Розглянемо двофакторну лінійну модель 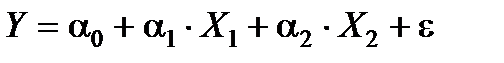 . Оцінимо її параметри на основі МНК. Оцінене рівняння моделі запишемо як
. Оцінимо її параметри на основі МНК. Оцінене рівняння моделі запишемо як 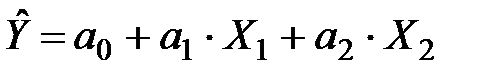 .
.
Система нормальних рівнянь для моделі множинної регресії має вигляд 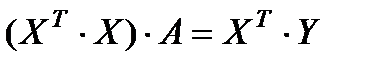 ,
,
звідки
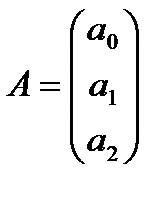 =
= 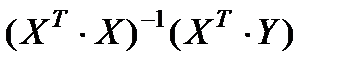 .
.
Виконаємо всі необхідні обчислення. Уведемо матрицю
X= 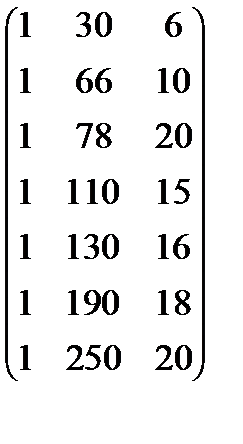 ,
,
тоді
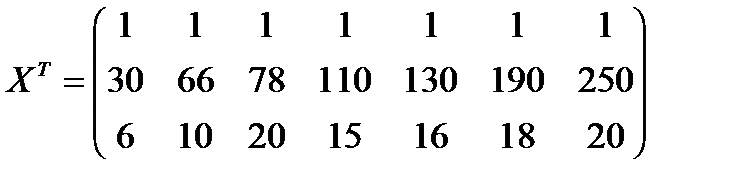 ;
;
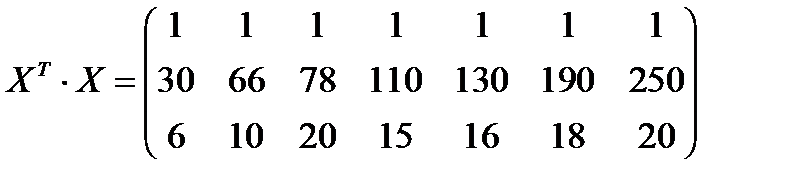 ·
· 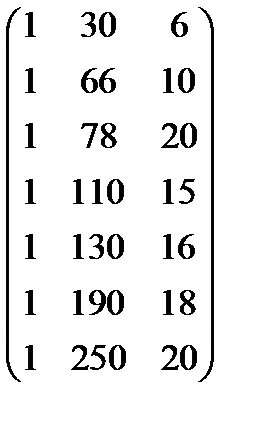 =
=  ;
; 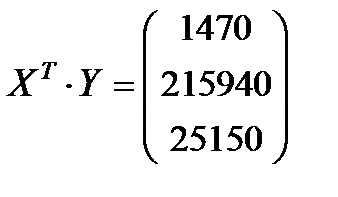 .
.
Запишемо таку систему нормальних рівнянь:
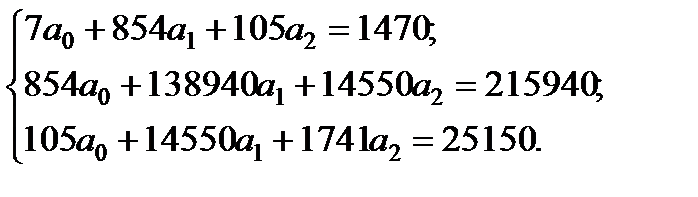
Для розв’язання системи методом оберненої матриці знайдемо таке:
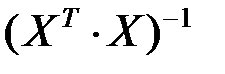 =
= 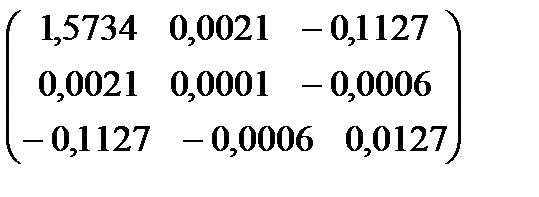 ,
,
звідки
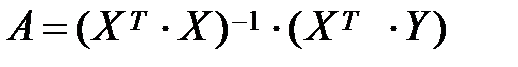 =
= 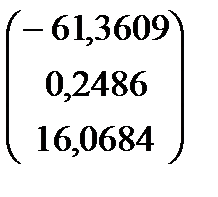 .
.
Отже, рівняння моделі має вигляд
Y = –61,36+0,25x1+16,07x2.
Оцінка параметра 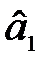 характеризує граничну зміну величини прибутку (Y) залежно від інвестиційних вкладень в оборотні кошти (X1) на одиницю. Тобто якщо інвестиційні вкладення в оборотні кошти зростуть на одиницю, то прибуток збільшиться на 0,25 одиниці за незмінного основного капіталу.
характеризує граничну зміну величини прибутку (Y) залежно від інвестиційних вкладень в оборотні кошти (X1) на одиницю. Тобто якщо інвестиційні вкладення в оборотні кошти зростуть на одиницю, то прибуток збільшиться на 0,25 одиниці за незмінного основного капіталу.
Оцінка параметра 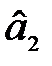 характеризує граничне зростання витрат прибутку (Y) залежно від інвестиційних вкладень в основний капітал (X2). Так, якщо інвестиційні вкладення в основний капітал збільшаться на одиницю, то прибуток зросте на 16,07 одиниці за незмінної величини інвестиційних вкладень в оборотні кошти.
характеризує граничне зростання витрат прибутку (Y) залежно від інвестиційних вкладень в основний капітал (X2). Так, якщо інвестиційні вкладення в основний капітал збільшаться на одиницю, то прибуток зросте на 16,07 одиниці за незмінної величини інвестиційних вкладень в оборотні кошти.
ІІ. Перевірка якості моделі
Зведемо всі показники, необхідні для розрахунку параметрів і характеристик моделі, у табл. 10.
Таблиця 10
| Номер
підприємства
| Y
| X1
| X2
| 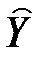
| 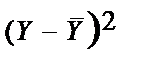
| 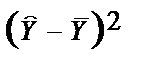
| e2
| Точність
|
| 1
| 50
| 30
| 6
| 42,51
| 25600
| 28053,27
| 56,12
| 14,98
|
| 2
| 120
| 66
| 10
| 115,73
| 8100
| 8886,12
| 18,20
| 3,56
|
| 3
| 290
| 78
| 20
| 279,40
| 6400
| 4816,57
| 112,33
| 3,65
|
| 4
| 190
| 110
| 15
| 207,02
| 400
| 8,90
| 289,55
| 8,96
|
| 5
| 200
| 130
| 16
| 228,06
| 100
| 326,08
| 787,23
| 14,03
|
| 6
| 300
| 190
| 18
| 275,11
| 8100
| 4239,73
| 619,35
| 8,30
|
| 7
| 320
| 250
| 20
| 322,17
| 12100
| 12581,85
| 4,70
| 0,68
|
| Сума
| 1470
| 854
| 105
| 1470
| 60800
| 58912,52
| 1887,48
| 54,15
|
| Середні
| 210
| 122
| 15
| –
| TSS
| ESS
| RSS
| 7,74%
|
1. Перевірка загальної якості моделі
Порівнявши дисперсію залишків і факторну дисперсію, бачимо, що
RSS<ЕSS, тому попередньо можна вважати, що досліджуване рівняння визначає адекватну модель.
Знайдемо коефіцієнт детермінації:
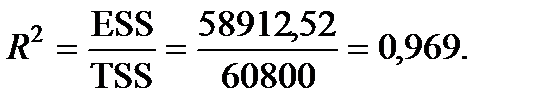
Розрахуємо скоригований коефіцієнт детермінації:
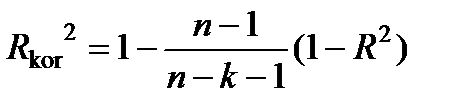 =
= 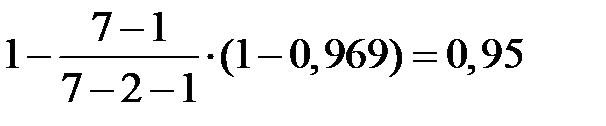 .
.
Обидва коефіцієнти свідчать про сильний зв’язок між факторними змінними та результативним показником. Варіація аналізованої залежної змінної 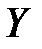 на 95% визначена зміною факторних змінних.
на 95% визначена зміною факторних змінних.
Перевіримо статистичну значущість рівняння в цілому на основі критерію Фішера. Розрахуємо статистику Фішера:
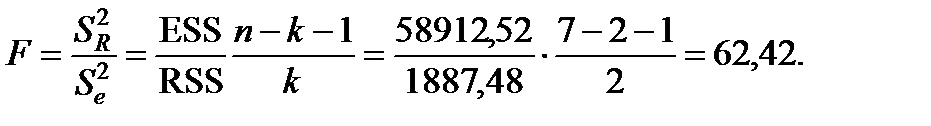
Табличне значення статистики складає Fтабл ( 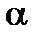 =0,05; 2,4)=6,94.
=0,05; 2,4)=6,94.
Оскільки розрахункове значення статистики F набагато більше критичного значення, можна визнати модель адекватною та надійною з імовірністю 95%.
2. Перевірка статистичної значущості параметрів моделі
Обчислимо коваріаційну матрицю 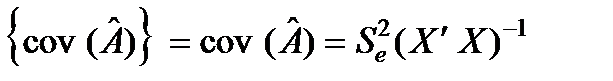 :
:
1) визначимо незміщену оцінку дисперсії залишків 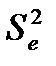 , застосувавши співвідношення
, застосувавши співвідношення
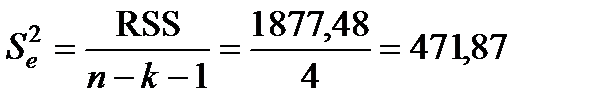 ;
;
2) знайдемо таке:
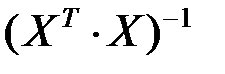 =
= 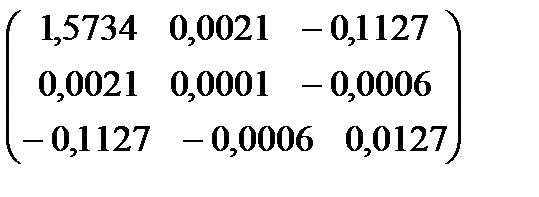 ;
;
3) отримаємо дисперсійно-коваріаційну матрицю
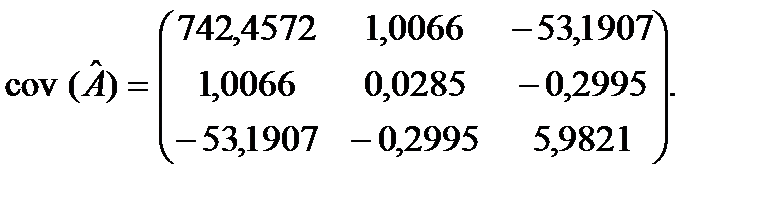
Із матриці визначимо дисперсії оцінок 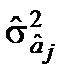 :
:
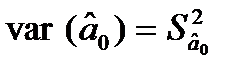 = 742,45;
= 742,45; 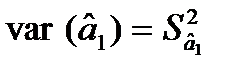 = 0,0285;
= 0,0285; 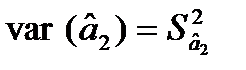 = 5,9821.
= 5,9821.
Коваріації відповідних оцінок параметрів становлять
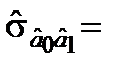 1,0066;
1,0066; 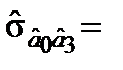 53,1907;
53,1907; 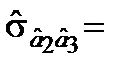 –0,2995.
–0,2995.
Знак «мінус» перед оцінками коваріацій указує на те, що зі збільшенням однієї оцінки параметрів інша зменшується в середньому і навпаки.
Обчислимо стандартні похибки оцінок параметрів моделі:
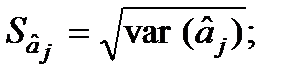
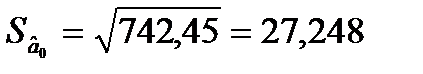 ;
; 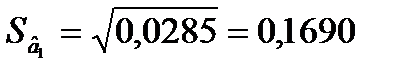 ;
; 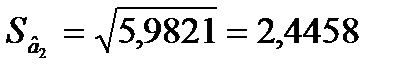 .
.
Стандартні похибки характеризують середні лінійні коливання оцінок параметрів моделі навколо свого математичного сподівання. Чим менші ці похибки, тим більш стійкі оцінки параметрів моделі. Але остаточні висновки стосовно стійкості оцінок можна зробити, порівнявши стандартні похибки з абсолютними значеннями оцінок параметрів моделі. Тому знайдемо 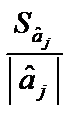 :
:
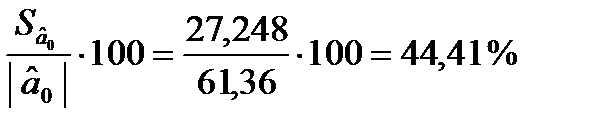 ;
; 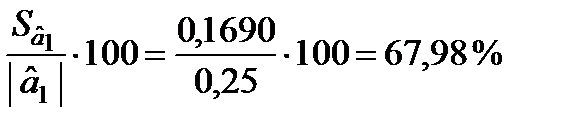 ;
; 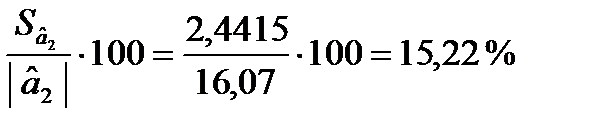 .
.
Отже, стандартні похибки оцінок параметрів відносно рівня самих оцінок становлять відповідно 44,41, 67,98 і 15,22 %, що свідчить про зміщення оцінок. Це означає, що залишки можуть мати систематичну складову, зумовлену неточною специфікацією моделі. Наприклад, не всі основні чинники, які впливають на результативний фактор, внесено до моделі.
Для перевірки статистичної значущості параметрів знайдемо статистики Стьюдента:
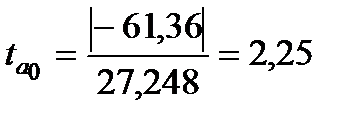 ;
; 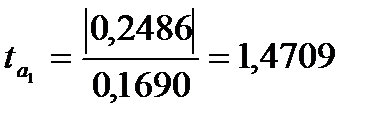 ;
; 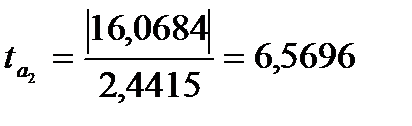 .
.
Теоретичне значення статистики Стьюдента складає
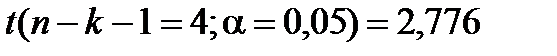 .
.
Для коефіцієнтів  та
та 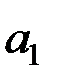 розрахункове значення статистики менше теоретичного, тому гіпотезу про рівність їх нулю відкинути не можна і ці коефіцієнти є статистично незначущі. Для коефіцієнта
розрахункове значення статистики менше теоретичного, тому гіпотезу про рівність їх нулю відкинути не можна і ці коефіцієнти є статистично незначущі. Для коефіцієнта 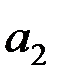
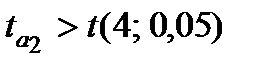 , тому статистична значущість коефіцієнта
, тому статистична значущість коефіцієнта 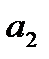 підтверджується.
підтверджується.
Отримані результати означають, що друга незалежна компонента (основний капітал) істотно впливає на залежну змінну (прибуток). Статистична незначущість коефіцієнта  вказує на те, що всі інші фактори, не враховані в регресійній моделі, не роблять значного впливу на залежну змінну. Також фактор інвестиційних вкладень в оборотні кошти не впливає сильно на результат – прибуток.
вказує на те, що всі інші фактори, не враховані в регресійній моделі, не роблять значного впливу на залежну змінну. Також фактор інвестиційних вкладень в оборотні кошти не впливає сильно на результат – прибуток.
3. Визначення точності моделі
Для характеристики точності розрахуємо середню відносну похибку апроксимації (див. табл. 10): 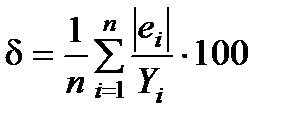 =7,74%. Ця величина не перевищує 10%, тому можна вважати точність моделі досить високою.
=7,74%. Ця величина не перевищує 10%, тому можна вважати точність моделі досить високою.
4. Аналіз впливу факторних змінних на результативний показник
1. Розрахуємо коефіцієнти еластичності:
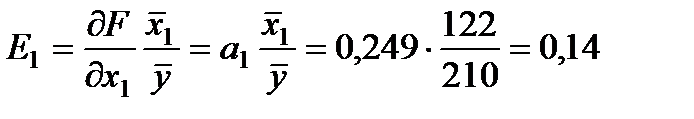 ;
; 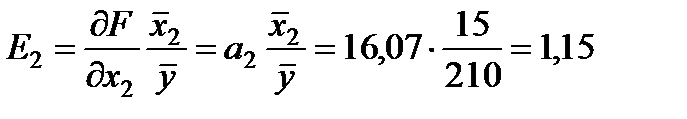 .
.
Це означає, що за збільшення внесків в оборотні кошти на 1% (фактор X1) і незмінної величини внесків в основний капітал прибуток зросте на 0,14%. У випадку збільшення внесків в основний капітал (фактор X2) на 1% прибуток зросте на 1,15%. Таким чином, інвестиційні вкладення в основний капітал більш значущі для виробництва.
2. Розрахуємо b-коефіцієнти. Для цього знайдемо середньоквадратичні відхилення для факторних змінних та результативного показника:
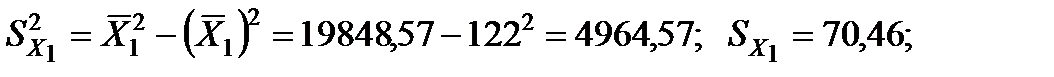
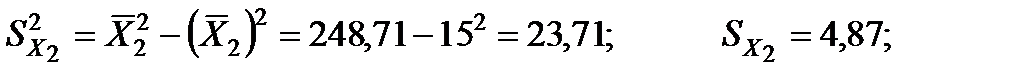
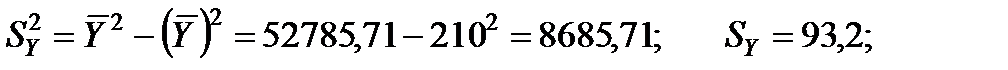
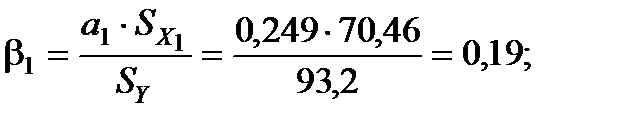
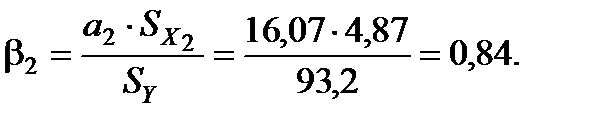
Отримані коефіцієнти показують, на яку частину величини середньоквадратичного відхилення зміниться в середньому значення залежної змінної у випадку зміни факторної ознаки на величину її середньоквадратичного відхилення.
3. Розрахуємо  -коефіцієнти:
-коефіцієнти: 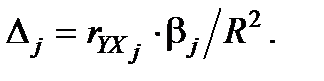 Для цього знайдемо коефіцієнти парної кореляції:
Для цього знайдемо коефіцієнти парної кореляції:
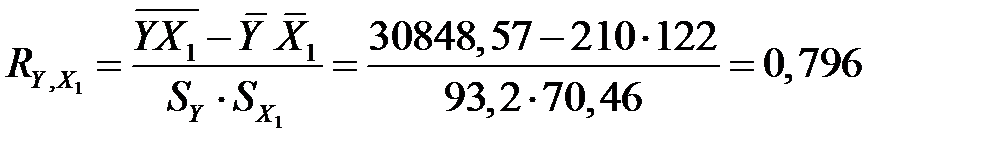 ;
;
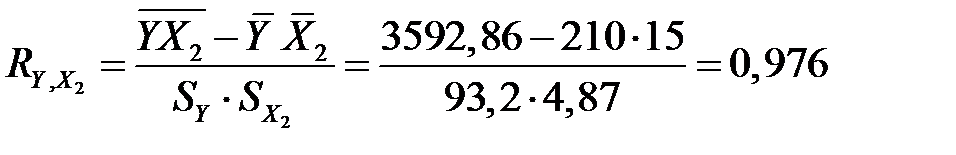 .
.
Тоді 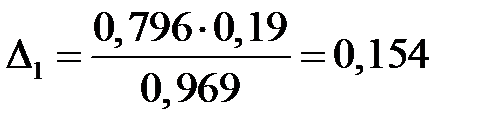 ;
; 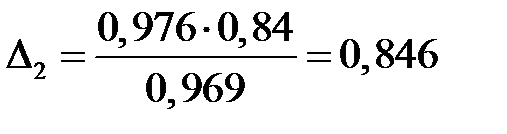 .
.
Це означає, що на 84,6% прирости прибутку підприємств можна пояснити вкладеннями в основний капітал і тільки на 15,4% – додатковими вкладеннями в оборотні кошти.





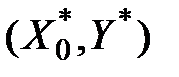 необхідно з'ясувати, чи задовольняє вона попередню залежність, тобто чи дорівнює
необхідно з'ясувати, чи задовольняє вона попередню залежність, тобто чи дорівнює 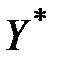 значенню
значенню 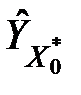 , отриманому підстановкою
, отриманому підстановкою 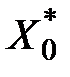 в рівняння моделі.
в рівняння моделі.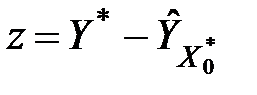 . Сформулюємо дві гіпотези:
. Сформулюємо дві гіпотези: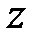 = 0, тобто значення
= 0, тобто значення 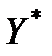 та
та 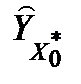 збігаються;
збігаються;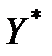 та
та 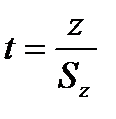 має розподіл Стьюдента з
має розподіл Стьюдента з 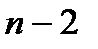 степенями вільності. Оцінку дисперсії величини z обчислимо за формулою
степенями вільності. Оцінку дисперсії величини z обчислимо за формулою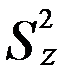 =
= 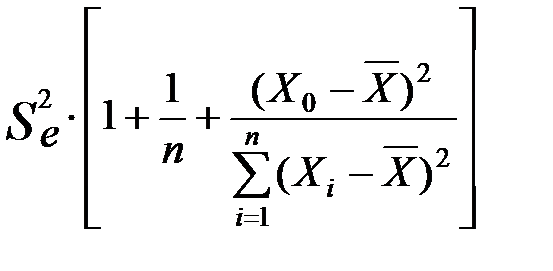 .
.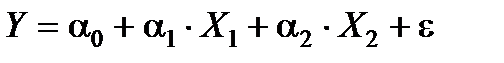 . Оцінимо її параметри на основі МНК. Оцінене рівняння моделі запишемо як
. Оцінимо її параметри на основі МНК. Оцінене рівняння моделі запишемо як 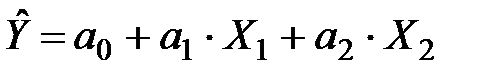 .
.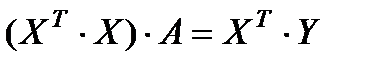 ,
,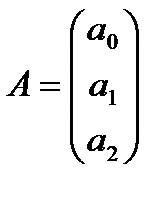 =
= 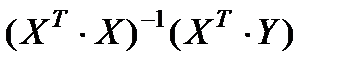 .
. ,
,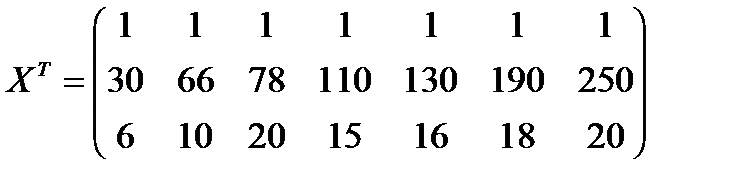 ;
;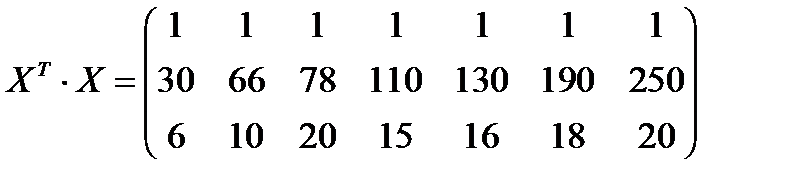 ·
·  =
=  ;
; 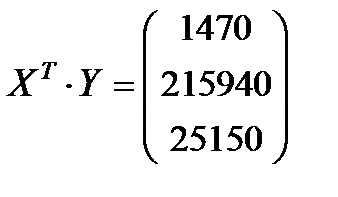 .
.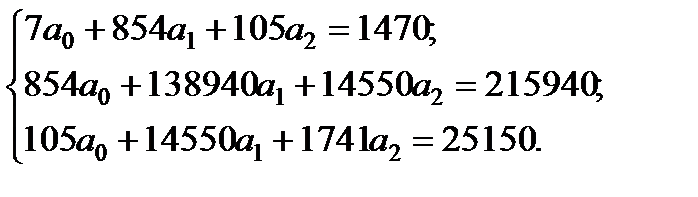
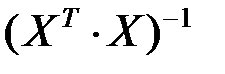 =
= 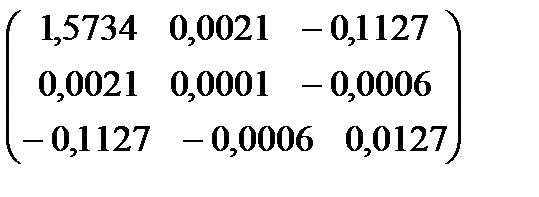 ,
,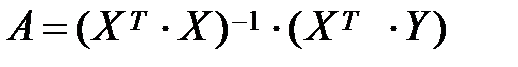 =
= 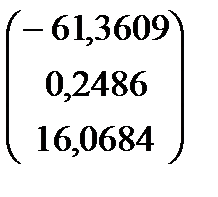 .
.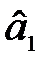 характеризує граничну зміну величини прибутку (Y) залежно від інвестиційних вкладень в оборотні кошти (X1) на одиницю. Тобто якщо інвестиційні вкладення в оборотні кошти зростуть на одиницю, то прибуток збільшиться на 0,25 одиниці за незмінного основного капіталу.
характеризує граничну зміну величини прибутку (Y) залежно від інвестиційних вкладень в оборотні кошти (X1) на одиницю. Тобто якщо інвестиційні вкладення в оборотні кошти зростуть на одиницю, то прибуток збільшиться на 0,25 одиниці за незмінного основного капіталу.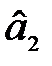 характеризує граничне зростання витрат прибутку (Y) залежно від інвестиційних вкладень в основний капітал (X2). Так, якщо інвестиційні вкладення в основний капітал збільшаться на одиницю, то прибуток зросте на 16,07 одиниці за незмінної величини інвестиційних вкладень в оборотні кошти.
характеризує граничне зростання витрат прибутку (Y) залежно від інвестиційних вкладень в основний капітал (X2). Так, якщо інвестиційні вкладення в основний капітал збільшаться на одиницю, то прибуток зросте на 16,07 одиниці за незмінної величини інвестиційних вкладень в оборотні кошти.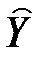
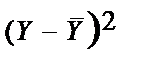
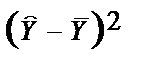
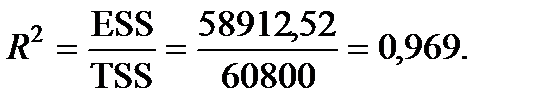
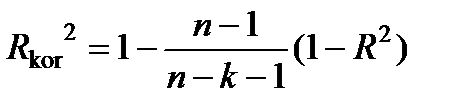 =
= 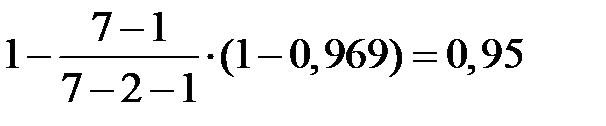 .
.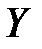 на 95% визначена зміною факторних змінних.
на 95% визначена зміною факторних змінних.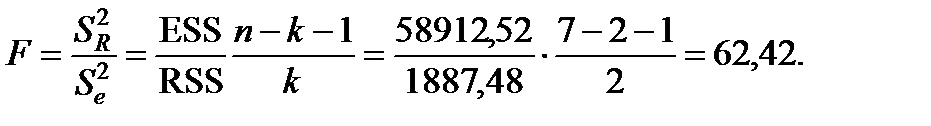
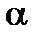 =0,05; 2,4)=6,94.
=0,05; 2,4)=6,94.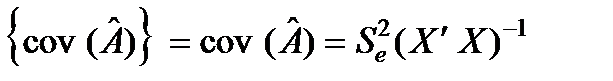 :
: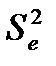 , застосувавши співвідношення
, застосувавши співвідношення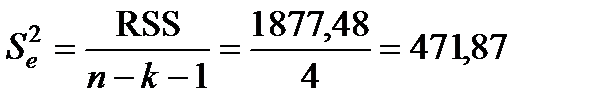 ;
;
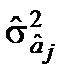 :
: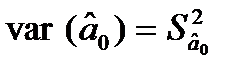 = 742,45;
= 742,45; 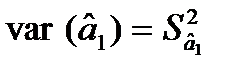 = 0,0285;
= 0,0285; 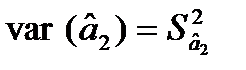 = 5,9821.
= 5,9821.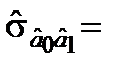 1,0066;
1,0066; 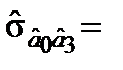 53,1907;
53,1907; 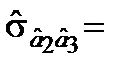 –0,2995.
–0,2995.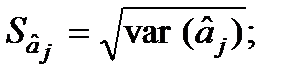
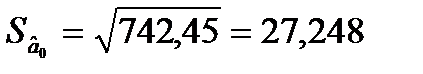 ;
; 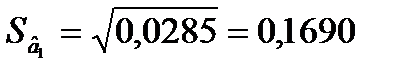 ;
; 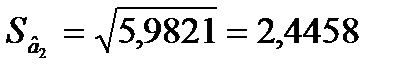 .
.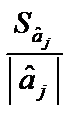 :
: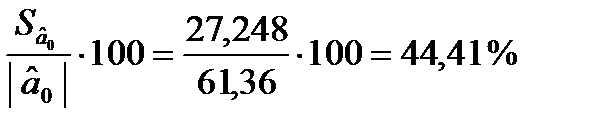 ;
; 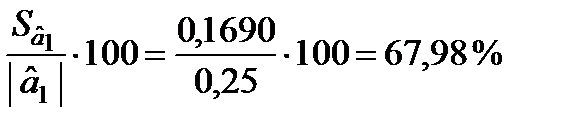 ;
; 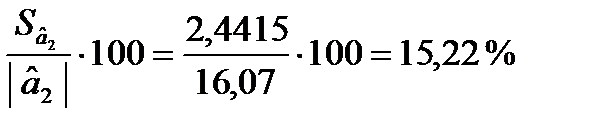 .
.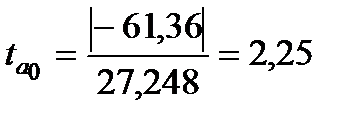 ;
; 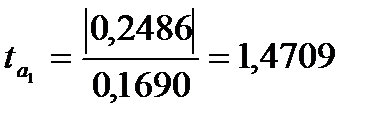 ;
; 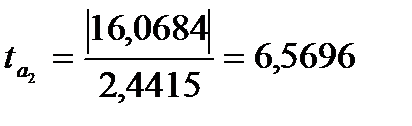 .
.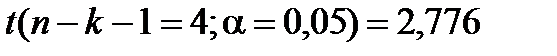 .
. та
та 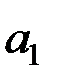 розрахункове значення статистики менше теоретичного, тому гіпотезу про рівність їх нулю відкинути не можна і ці коефіцієнти є статистично незначущі. Для коефіцієнта
розрахункове значення статистики менше теоретичного, тому гіпотезу про рівність їх нулю відкинути не можна і ці коефіцієнти є статистично незначущі. Для коефіцієнта 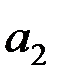
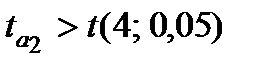 , тому статистична значущість коефіцієнта
, тому статистична значущість коефіцієнта 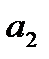 підтверджується.
підтверджується.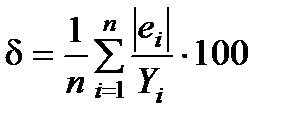 =7,74%. Ця величина не перевищує 10%, тому можна вважати точність моделі досить високою.
=7,74%. Ця величина не перевищує 10%, тому можна вважати точність моделі досить високою.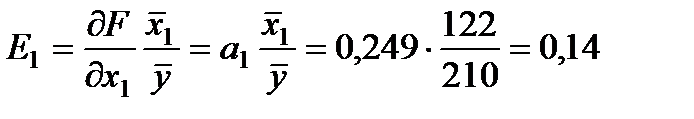 ;
; 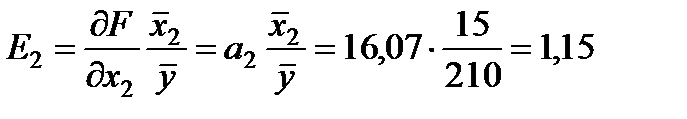 .
.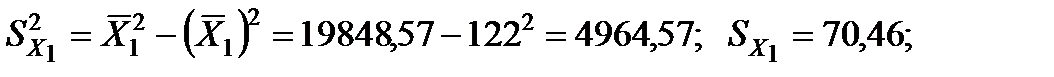
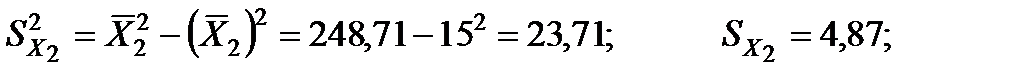
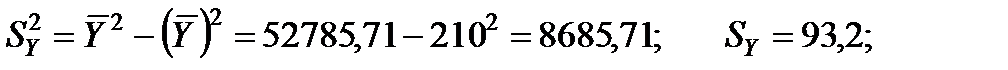
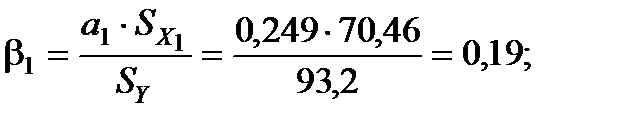
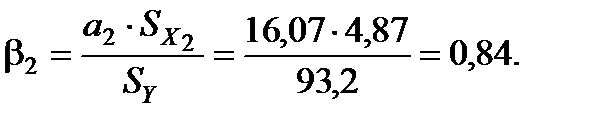
 -коефіцієнти:
-коефіцієнти: 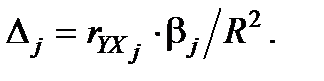 Для цього знайдемо коефіцієнти парної кореляції:
Для цього знайдемо коефіцієнти парної кореляції: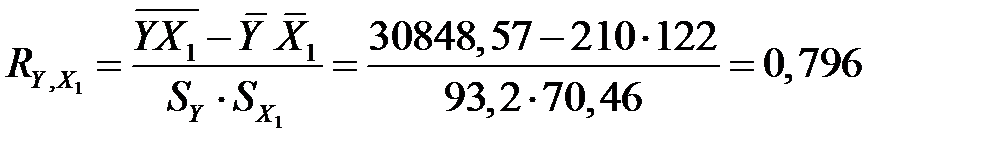 ;
;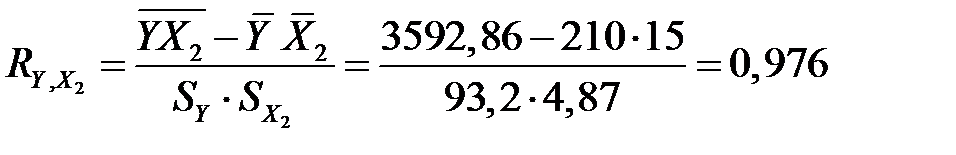 .
.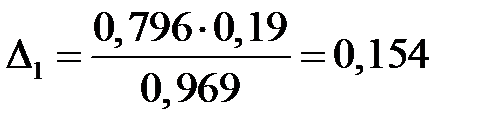 ;
; 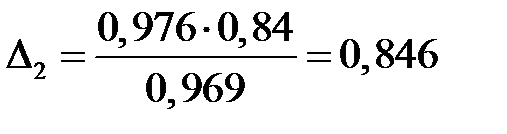 .
.
