Парний коефіцієнт кореляції між будь-якими двома змінними, наприклад між Х і Y, визначають за формулою
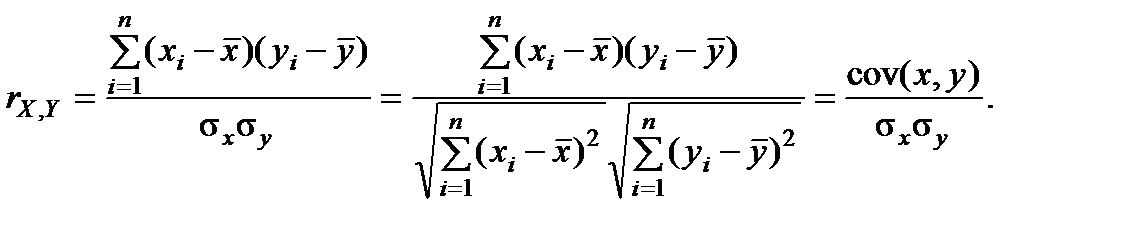
Зауваження. Оскільки в чисельнику маємо коефіцієнт коваріації між відповідними змінними, а в знаменнику – їх стандартні відхилення, слід пам’ятати, що кореляція – це просто нормована коваріація між цими змінними, але на відміну від останньої завдяки нормуванню вона не залежить від розмірності цих змінних (тобто є безрозмірна, отже, універсальна для зіставлень).
Повний перелік парних коефіцієнтів кореляції складає так звану кореляційну матрицю r:
r = 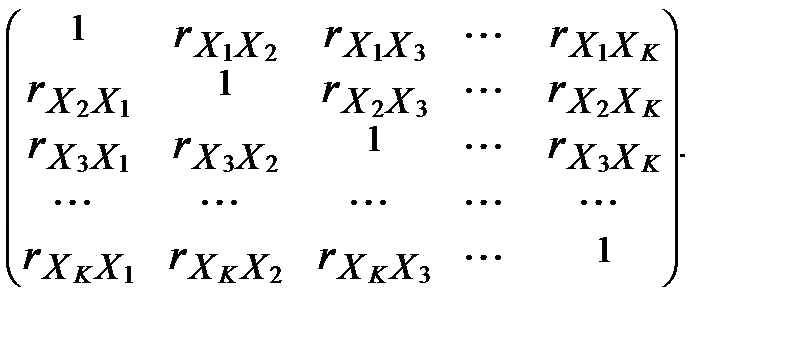
Кореляційна матриця завжди симетрична відносно головної діагоналі. Елементи головної діагоналі завжди дорівнюють одиниці.
Кореляційну матрицю можна розрахувати із застосуванням формули
r= (Y*·X*)T (Y*·X*),
де (Y*·X*) – матриця, складена зі стовпців стандартизованих змінних Y і X.
Стандартизація – перетворення вихідних даних на безрозмірні величини з середнім значенням 0 і стандартним відхиленням 1. При цьому всі властивості вихідних даних (зміни динаміки, пропорції тощо) зберігаються і для стандартизованих. Стандартизація включає дві процедури – центрування даних (тобто зміщення середини ряду на початок координат) і нормалізацію даних (ділення їх на певну величину), тобто масштабування.
Ми будемо використовувати як масштаб стандартне відхилення ряду. Таким чином, перетворення виконаємо згідно з формулами 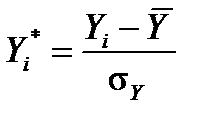 ,
, 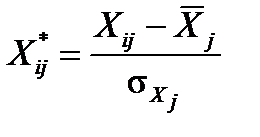 , де
, де 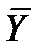 – середнє значення (дод. 1) змінної Y;
– середнє значення (дод. 1) змінної Y; 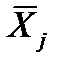 – середнє значення змінної Xj;
– середнє значення змінної Xj; 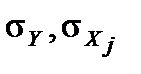 – стандартні відхилення змінних Y і Xj відповідно.
– стандартні відхилення змінних Y і Xj відповідно.
Стандартні відхилення розраховуємо за формулою (приклад для
змінної Y):
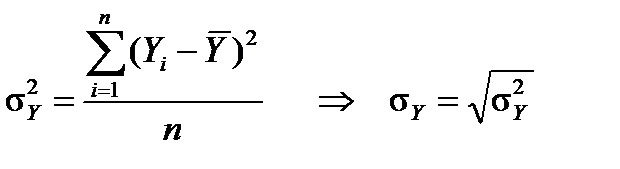 .
.
Зауваження.
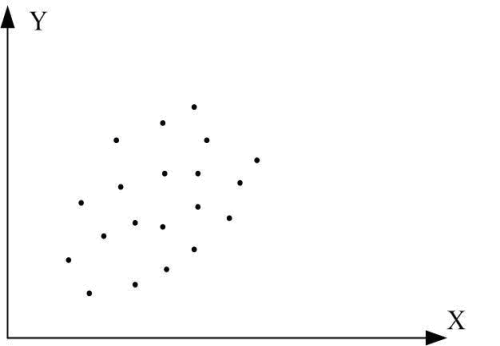
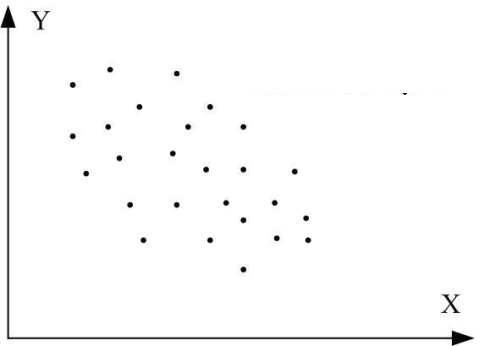
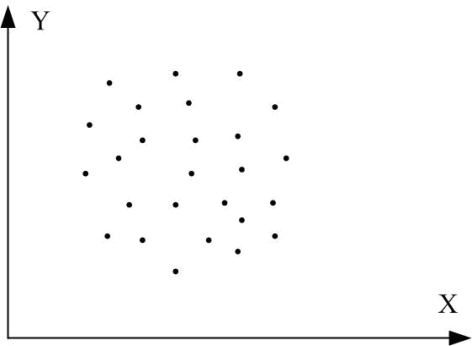
1. Коефіцієнт кореляції може набувати значень від мінус одиниці до одиниці, тобто 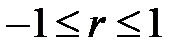 . Чим ближче значення r до одиниці за модулем, тим тісніший зв’язок. Від’ємний знак свідчить про зворотний зв’язок (рис. 1, б, г), додатний – про прямий (рис. 1, а, в). Якщо змінні статистично незалежні, коефіцієнт кореляції між ними дорівнює нулю (рис. 1, д – ж).
. Чим ближче значення r до одиниці за модулем, тим тісніший зв’язок. Від’ємний знак свідчить про зворотний зв’язок (рис. 1, б, г), додатний – про прямий (рис. 1, а, в). Якщо змінні статистично незалежні, коефіцієнт кореляції між ними дорівнює нулю (рис. 1, д – ж).

а б в
г д е
є ж
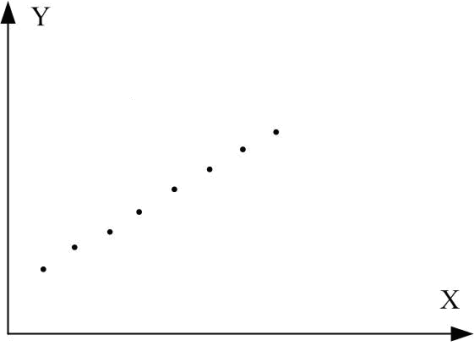
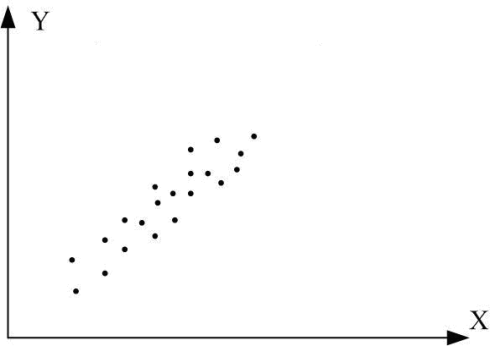
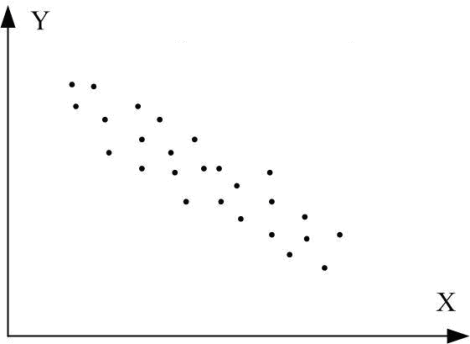
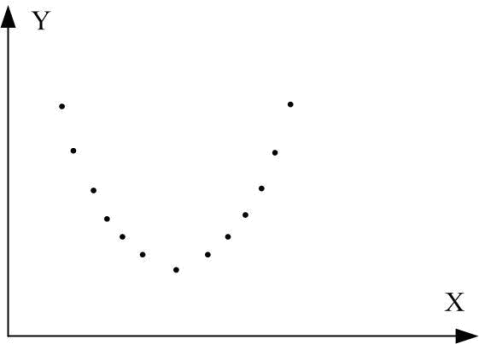
Рис. 1. Графіки кореляційного зв’язку для різних випадків вибірок:
а) r=1; б) r= –1; в) r близький до одиниці; г) r близький до –1;
д) r додатний, близький до нуля; е) r від’ємний, близький до нуля;
є) r=0; ж) r=0.
2. Оскільки коефіцієнт кореляції характеризує щільність тільки лінійної залежності, він незастосовний для опису нелінійної залежності. Так, на рис. 1, ж є точна залежність Y=X2, хоч 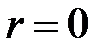 . Таким чином, нульовий коефіцієнт кореляції не обов’язково означає незалежність.
. Таким чином, нульовий коефіцієнт кореляції не обов’язково означає незалежність.
3. За своєю природою коефіцієнт кореляції симетричний, тобто кореляція між Х і Y (rXY) така ж, що й між Y і Х (rYX).
4. Хоч r є міра лінійної асоціативності між двома змінними, це не обов’язково означає існування якого-небудь причинно-наслідкового зв’язку. Треба уникати так званих хибних кореляцій, тобто не можна пов’язувати явища, між якими відсутні реальні причинно-наслідкові зв'язки.
Частинні коефіцієнти кореляції визначають для випадку, коли доводиться враховувати той факт, що на щільність зв’язку між двома змінними можуть впливати інші змінні (оскільки вони, у свою чергу, можуть мати істотний зв’язок із заданими змінними).
Для того щоб оцінити «чисту» щільність зв’язку між парою змінних, розраховують частинний коефіцієнт кореляції – коефіцієнт кореляційного зв’язку між двома змінними, очищеного від впливу інших змінних.
Розглядуваний коефіцієнт позначають як ry,xi|x1,...,хn, де до вертикальної риски вказують, для яких змінних знаходять частинний коефіцієнт кореляції, а після неї – вплив яких змінних при цьому ігнорують (говорять, що ці змінні є фіксовані).





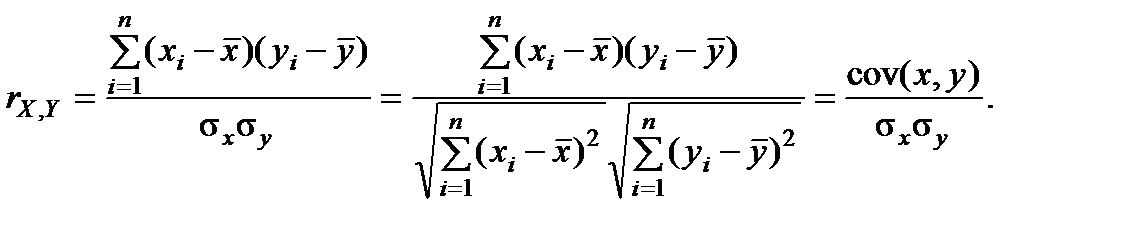
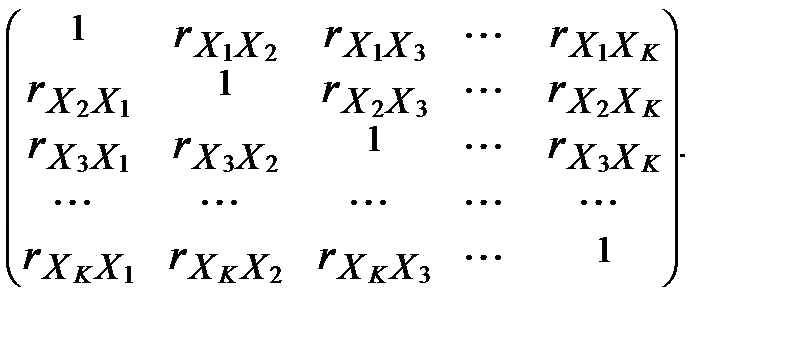
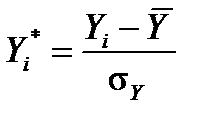 ,
, 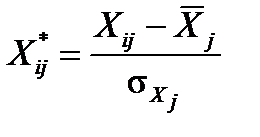 , де
, де 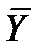 – середнє значення (дод. 1) змінної Y;
– середнє значення (дод. 1) змінної Y; 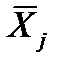 – середнє значення змінної Xj;
– середнє значення змінної Xj; 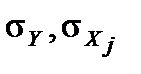 – стандартні відхилення змінних Y і Xj відповідно.
– стандартні відхилення змінних Y і Xj відповідно.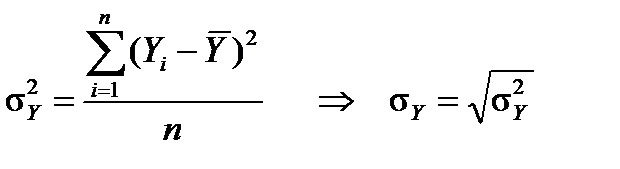 .
.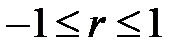 . Чим ближче значення r до одиниці за модулем, тим тісніший зв’язок. Від’ємний знак свідчить про зворотний зв’язок (рис. 1, б, г), додатний – про прямий (рис. 1, а, в). Якщо змінні статистично незалежні, коефіцієнт кореляції між ними дорівнює нулю (рис. 1, д – ж).
. Чим ближче значення r до одиниці за модулем, тим тісніший зв’язок. Від’ємний знак свідчить про зворотний зв’язок (рис. 1, б, г), додатний – про прямий (рис. 1, а, в). Якщо змінні статистично незалежні, коефіцієнт кореляції між ними дорівнює нулю (рис. 1, д – ж).







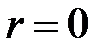 . Таким чином, нульовий коефіцієнт кореляції не обов’язково означає незалежність.
. Таким чином, нульовий коефіцієнт кореляції не обов’язково означає незалежність.

