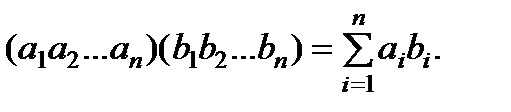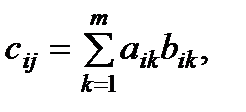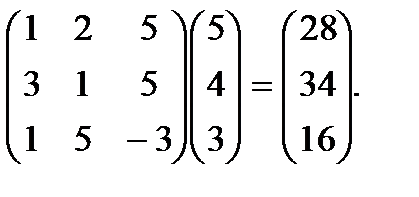Основні відомості про роботу зі статистичними

Та матричними функціями Excel

У MS Excel є низка спеціальних функцій, призначених для обчислення вибіркових характеристик. Це функції, що характеризують центр розподілу:

- СРЗНАЧ – обчислює середнє арифметичне з декількох масивів (аргументів) чисел;

- МЕДИАНА – дозволяє отримувати медіану заданої вибірки;

- МОДА – обчислює значення, яке найбільш часто зустрічається у вибірці.

До спеціальних функцій обчислення вибіркових показників, що характеризують розсіювання варіант, належать ДИСП і СТАНДОТКЛОН.

Функція ДИСП дозволяє оцінити дисперсію за вибірковими даними.

Функція СТАНДОТКЛОН обчислює стандартне відхилення.

Функція ЭКСЦЕСС обчислює оцінку ексцесу за вибірковими даними.

Функція СКОС дозволяє оцінити асиметрію вибіркового розподілу.

У MS Excel з матрицями можна працювати як з діапазоном комірок. Можна застосовувати формули, результатом яких є не одне число, а діапазон чисел. Це так звані формули масиву. Для введення таких формул необхідно виконати такі дії:

1) виділити комірки, у які буде поміщено результат виконання формули;

2) ввести формулу масиву (починаючи зі знака «=»);

3) натиснути комбінацію клавіш Ctrl+Shift+Enter для завершення введення (для цього натискають і утримують клавіші Ctrl+Shift і потім короткочасно натискають клавішу Enter).

Уведені формули масиву відображаються в рядку формул у фігурних дужках.

Для зміни (або видалення) введеної раніше формули масиву необхідно попередньо виділити весь діапазон комірок цієї формули, а потім виконати бажану дію. Частину комірок формули масиву змінити не можна.

Результатом складання (віднімання) матриць (векторів) А і В однакового розміру n x m (кількості стовпців і рядків матриць повинні збігатися) є матриця C розміру n x m, кожен елемент якої дорівнює сумі (або різниці) відповідних елементів матриць A і B. Нижче наведено робочий аркуш з прикладом складання двох векторів-стовпців, заданих у комірках A2:A5 і C2:C5, сумарний вектор одержано в комірках E2:E5 (рис. І).

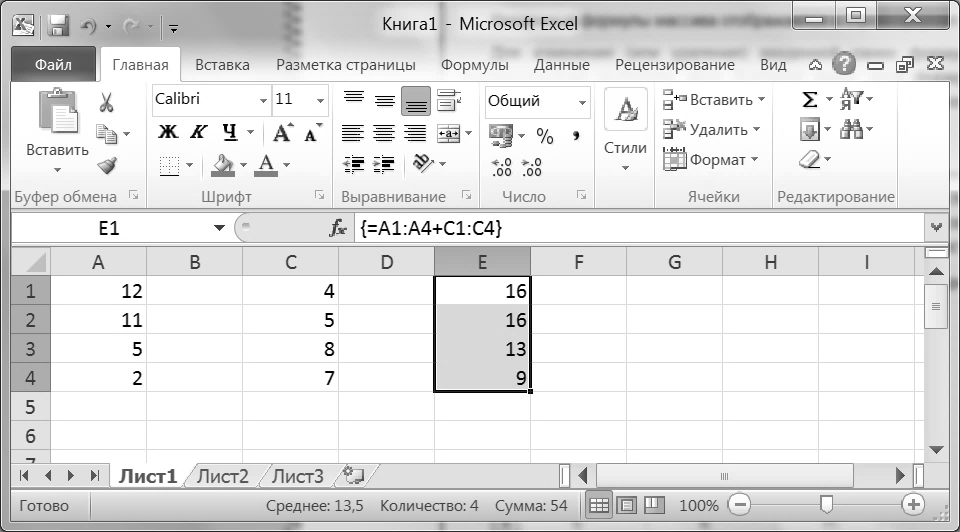
Рис. І. Приклад обчислення суми матриць (векторів) в MS Excel

Скалярним добутком двох векторів однакової довжини n називають суму парних добутків відповідних компонентів вектора:

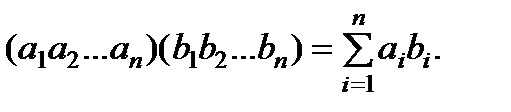
Для цієї операції можна застосовувати вбудовану функцію СУММПРОИЗВ. У цієї функції два параметри, відокремлювані крапкою з комою. Оскільки результат обчислень – це одне число, то формулу вводять в одну комірку (рис. ІІ).

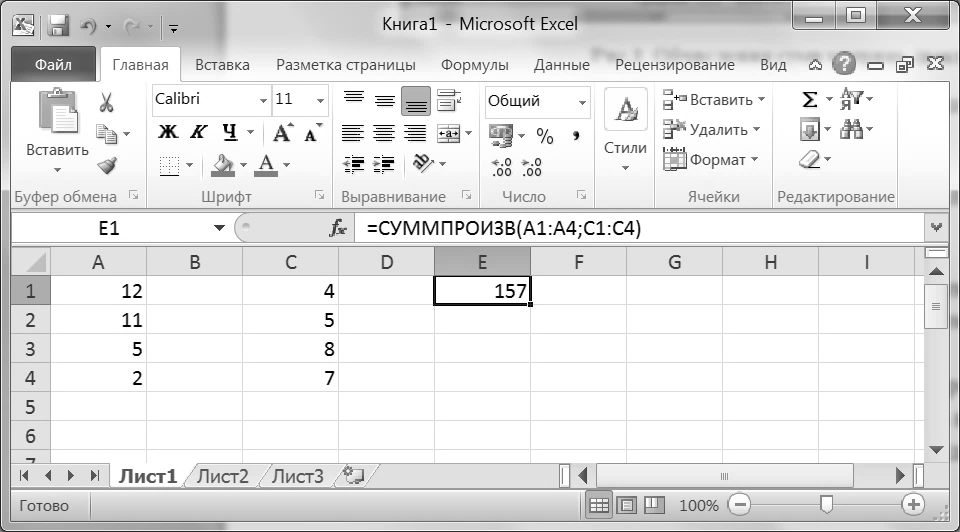
Рис. ІІ. Приклад обчислення суми добутків чисел в MS Excel

Добутком матриць A розміром n x m і B розміром m x l називають матрицю C розміром n x l, таку що елемент, який знаходиться на перетині i-го рядка і j-го стовпця c_ij дорівнює скалярному добутку i-го рядка матриці A і
j-го стовпця матриці B:

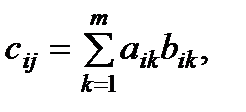
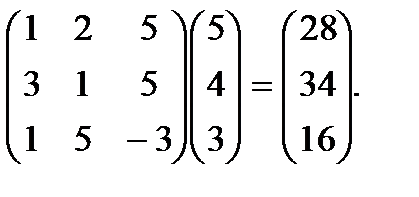
У MS Excel для матричного множення застосовують вбудовану функцію МУМНОЖ. У неї два параметри, що відповідають двом діапазонам, які містять перемножувані матриці. Результат функції – це матриця, тому вводити її в діапазон комірок слід як функцію масиву (рис. ІІІ).

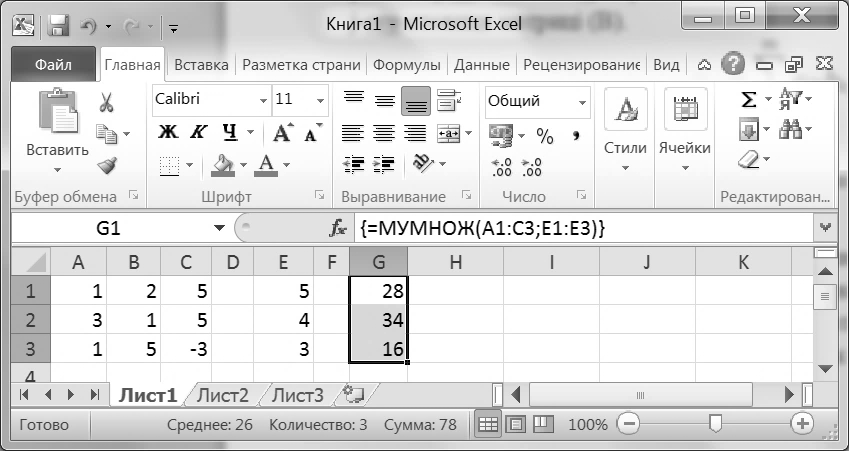
Рис. ІІІ. Приклад обчислення добутку матриць в MS Excel

Матрицею, оберненою до матриці А розміру n x n, називають матрицю А^-1 розміру n x n, таку що у випадку перемножування цих матриць у будь-якому порядку одержують одиничну діагональну матрицю:

АА^-1= А^-1А =1,

де 1 – це одинична діагональна матриця розміру n x n, всі елементи якої дорівнюють нулю, за винятком діагональних, що дорівнюють одиниці.

Знаходження оберненої матриці виконує вбудована функція МОБР. У неї єдиний аргумент, який є діапазоном, що містить обернену матрицю. Функція повертає матрицю, що дорівнює за розміром матриці, для якої обчислюють обернену, тому її слід вводити як функцію масиву (рис. ІV).

 

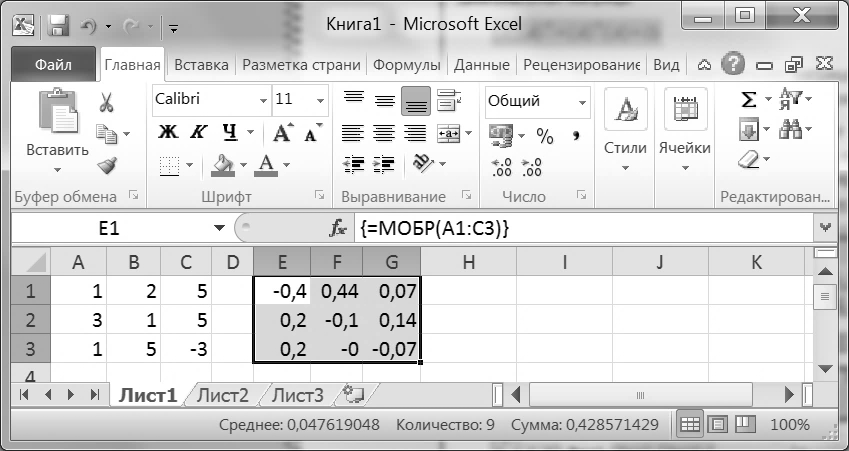
Рис. ІV. Приклад обчислення оберненої матриці в MS Excel

Знаходження визначника матриці виконує вбудована функція МОПРЕД. У неї єдиний параметр – діапазон, що містить матрицю, визначник якої треба знайти. Наприклад, формула = МОПРЕД (B2: D4) обчислює визначник матриці розміру 3 x 3, записаної в діапазоні B2: D4.

Додаток 3