Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Навигация:

Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Новые материалы

Топ:

Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...

Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...

Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из по­вторяющихся рабочих циклов, каждый из которых соответствует...

Интересное:

Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...

Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...

Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...

Дисциплины:

Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция

Приклад виконання розрахунків

2024-02-15 96
Приклад виконання розрахунків 0.00 из 5.00 0 оценок
Заказать работу

Вверх
Содержание
⇐ ПредыдущаяСтр 4 из 22Следующая ⇒
Поиск

На середньомісячну заробітну плату впливає низка факторів. Виділимо серед них продуктивність праці, фондомісткість та коефіцієнт плинності робочої сили. Визначимо, чи є між цими факторами тісний зв’язок. Вихідні дані наведено
в табл. 1.

Таблиця 1

Номер цеху Продуктивність праці, млн грн / люд. Фондомісткість, грн /грн Коефіцієнт плинності робочої сили, %
1 32 0,59 10,5
2 29 0,43 15,5
3 30 0,70 13,5
4 31 0,61 9,5
5 25 0,51 2,5
6 34 0,51 1,5
7 29 0,65 17,5
8 24 0,43 14,5
9 20 0,51 14,5
10 35 0,92 7,5

 

Розв’язування

Крок 1. Стандартизуємо змінні. Позначимо вектори незалежних змінних – продуктивності праці, фондомісткості, коефіцієнта плинності робочої сили – через Х1, Х2, Х3 відповідно. Елементи стандартизованих векторів розрахуємо за формулою

 

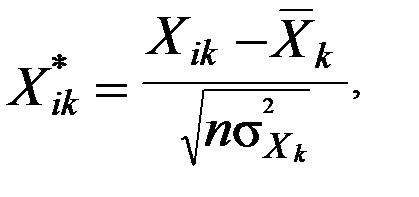
де n – кількість спостережень, n=10; k – кількість незалежних змінних, k=3;
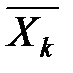– середнє арифметичне вектора 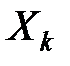; 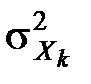– дисперсія змінної  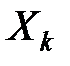(дод. 1).

Середні значення змінних становлять

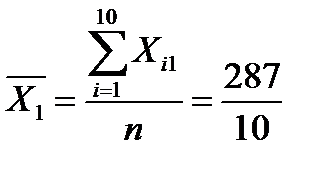=28,7; 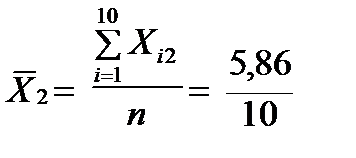=0,586; 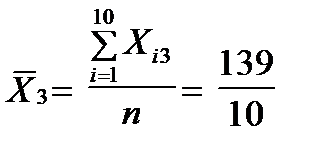=13,9.

Дисперсії кожної незалежної змінної мають такі значення:

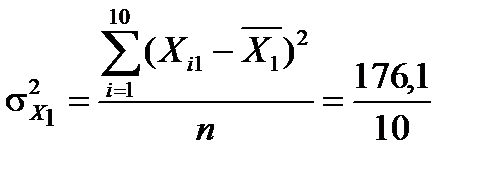=17,61; 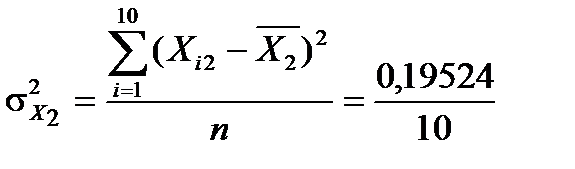=0,0195;

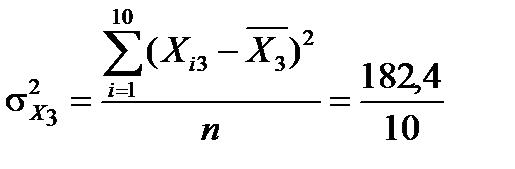=18,24.

У табл. 2 подано всі розрахунки, стосовні стандартизації незалежних змінних X1, X2, X3 згідно з наведеним співвідношенням.

 

    


 

Таблиця 2

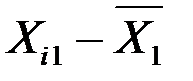
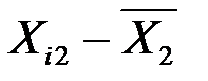
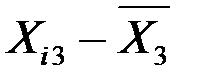
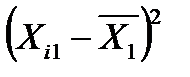
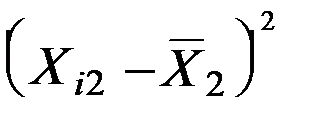
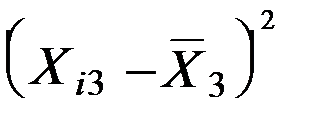
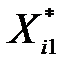
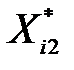
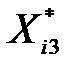
3,3 0,004 –3,4 10,89 0,000015 11,56  0,2487 0,0091 –0,2518
0,3 –0,156 1,6 0,09 0,024336 2,56  0,0226 –0,2531 0,1185
1,3 0,114 –0,4 1,69 0,012996 0,16  0,0979 0,2580 –0,0296
2,3 0,024 –4,4 5,29 0,000576 19,36  0,1733 0,0543 -0,3258
3,7 –0,076 9,6 13,09 0,005776 92,16 –0,2788 –0,1720 0,7108
5,3 –0,076 –1,4 23,09 0,005776 1,96 0,3994 –0,1720 –0,1037
0,3 0,064 3,5 10,09 0,004095 12,95 0,0226 0,1448 0,2666
–4,7 –0,156 0,6 22,09 0,024336 0,36 –0,3542 –0,3531 0,0444
–8,7 –0,076 0,6 75,69 0,005776 0,36 –0,6556 –0,1720 0,0444
4,3 0,334 –6,4 14,49 0,111556 40,95 0,3240 0,7559 –0,4739
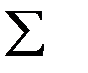
    17,6 0,19524 182,4      

Матриця стандартизованих змінних матиме вигляд

X*= .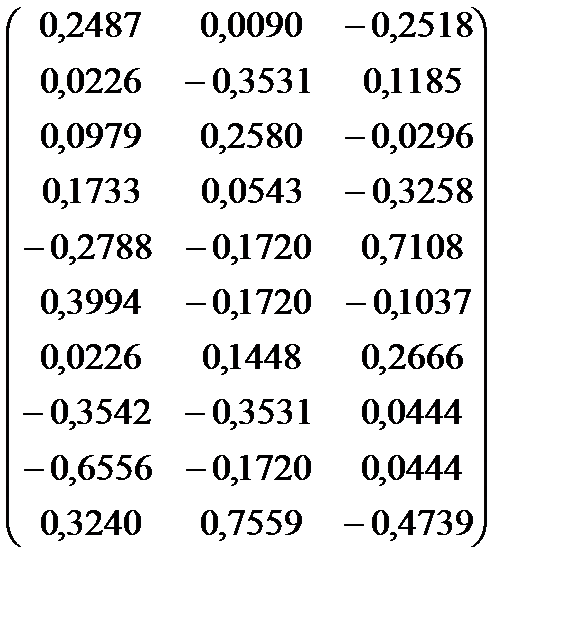

Крок 2. Знайдемо кореляційну матрицю r:

r = X *T × X *,

де 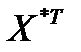– матриця, транспонована до матриці .

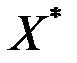Ця матриця симетрична і має розмір 3х3 для розглядуваної задачі:

r= .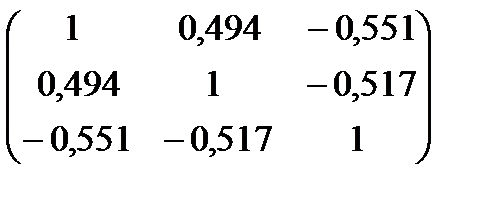

Кожен елемент цієї матриці характеризує щільність зв’язку однієї незалежної змінної з іншою. Оскільки діагональні елементи характеризують щільність зв’язку кожної незалежної змінної з цією самою змінною, то вони дорівнюють одиниці. Інші елементи матриці r є парними коефіцієнтами кореляції незалежних змінних, тобто , , .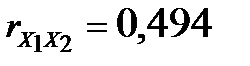

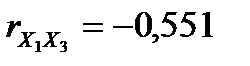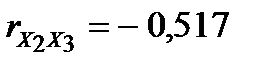Таким чином, можна зробити висновок, що між змінними X1, X2, X3 існує зв’язок.

Kрок 3. Розрахуємо частинні коефіцієнти кореляції, використавши елементи матриці С:

;

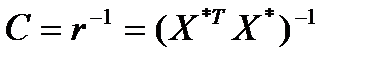С = .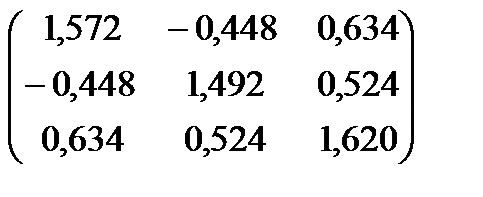

Тоді

; ;

.

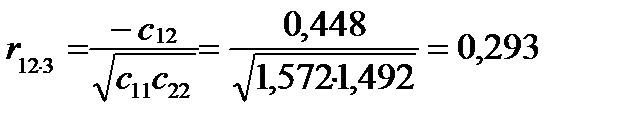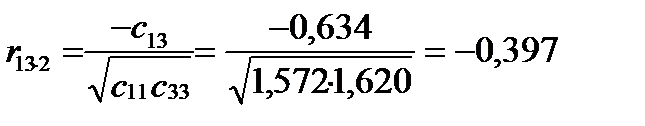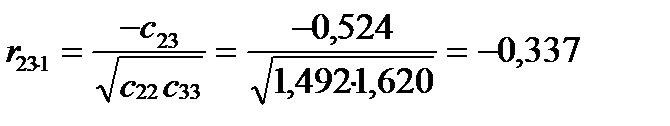Частинні коефіцієнти кореляції характеризують щільність зв’язку між двома змінними за умови, що третя не впливає на цей зв’язок.

Як бачимо, зв’язок не значний. Порівнявши частинні коефіцієнти кореляції з парними, наведеними вище, можна помітити, що частинні коефіцієнти значно менші парних.

Крок 4. Перевіримо статистичну значущість коефіцієнтів кореляції. Для парних коефіцієнтів кореляції визначимо t-критерії:

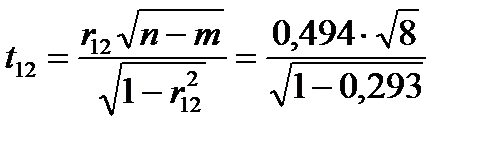=1,21; 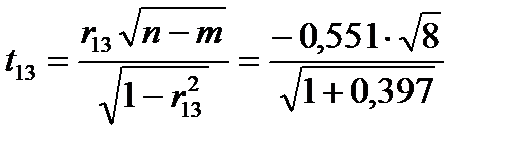= –1,32;

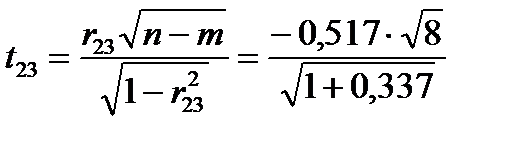= – 1,26.

Табличне значення t-критерію за n – m = 8 степенів вільності й за рівня значущості a = 0,05 дорівнює 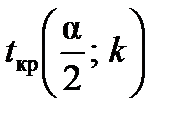=2,31.

Оскільки всі числові значення t-критеріїв, знайдених для кожної пари змінних, менші за їх табличне значення, то приймаємо гіпотезу про статистичну незначущість коефіцієнтів кореляції. Робимо висновок, що всі пари незалежних змінних не є тісно пов’язані.

Для частинних коефіцієнтів кореляції визначимо t-критерії:

; ;

.

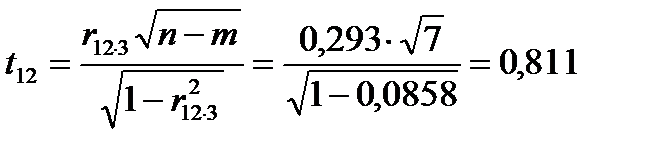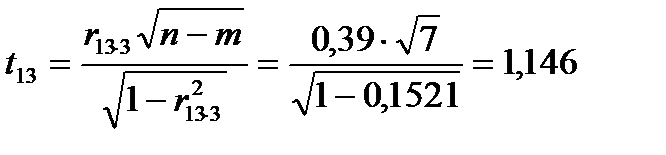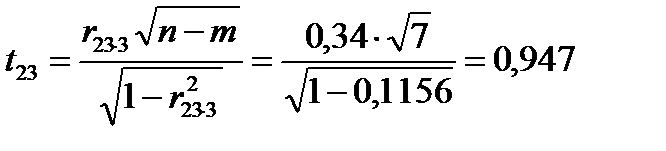Табличне значення t-критерію за n – m = 7 степенів вільності і рівня значущості a = 0,05 дорівнює 1,89.

Усі числові значення t-критеріїв, знайдених для кожної пари змінних, менші за їх табличне значення. Звідси робимо висновок, що всі пари незалежних змінних не є тісно пов’язані, тобто приймаємо гіпотезу про статистичну незначущість коефіцієнтів кореляції.

Зауваження. Під час виконання розрахунків можна застосувати статистичні й матричні функції електронних таблиць (дод. 2).

Завдання для самостійної роботи

Нехай на витрати обігу впливають: обсяг вантажообороту, запаси та трудомісткість одиниці вантажообороту. Дослідити наявність залежності між цими факторами на основі даних, наведених у таблицях за варіантами. Виконати такі завдання:

1) розрахувати для даних відповідного варіанта кореляційну матрицю, пояснити знайдені значення;

2) обчислити частинні коефіцієнти кореляції за допомогою матричних операторів, пояснити їх зміст;

3) оцінити статистичну значущість отриманих коефіцієнтів кореляції.

Варіант 1

  

Варіант 2

  
№ з/п Вантажо-оборот Запаси Трудо-місткість   № з/п

Вантажо-оборот

 Запаси

Трудо-місткість

  
1 15,6 40,4 2,11   1

15,1

 32,0

2,12

  
2 13,5 38,9 2,78   2

16,1

 32,4

1,98

  
3 15,3 36,6 2,17   3

16,7

 32,6

1,96

  
4 14,9 41,4 2,15   4

15,5

 38,7

2,15

  
5 15,1 32,2 2,11   5

17,2

 44,3

2,02

  
6 16,1 31,4 1,97   6

16,9

 39,3

2,05

  
7 16,7 32,6 1,96   7

17,0

 40,4

2,02

  
8 15,4 38,7 2,12   8

16,2

 41,5

2,13

  
9 17,1 44,3 2,02   9

15,0

 45,2

2,14

  
10 16,8 39,3 2,13   10

18,0

 50,2

1,90

  

Варіант 3

Варіант 4
№ з/п Вантажо-оборот Запаси Трудо­місткість   № з/п Вантажо-оборот

Запаси

Трудо-місткість
1 16,9 39,2 2,02   1 17,2

51,8

2,48
2 16,2 41,0 2,13   2 17,1

50,4

1,95
3 15,5 41,3 2,14   3 16,5

48,0

1,92
4 18,2 45,2 1,89   4 16,8

48,6

1,96
5 17,3 50,2 2,48   5 14,5

49,8

2,68
6 17,1 51,6 1,94   6 17,2

45,0

2,22
7 16,4 48,0 1,93   7 17,1

40,4

2,23
8 16,7 48,6 1,96   8 17,9

41,7

2,15
9 14,2 49,8 2,57   9 16,2

38,8

2,41
10 17,2 45,0 2,21   10 17,3

40,6

2,25
                       

 


Варіант 5

Варіант 6

  
№ з/п Вантажо-оборот Запаси Трудо-місткість   № з/п

Вантажо-оборот
Запаси

Трудо-місткість

  
1 14,3 49,8 2,68   1

17,8

 41,8

2,17

  
2 17,2 45,2 2,21   2

16,3

 38,7

2,40

  
3 17,0 41,4 2,24   3

17,2

 40,5

2,24

  
4 17,8 41,7 2,15   4

16,8

 34,6

2,13

  
5 16,3 38,7 2,41   5

14,9

 13,9

2,55

  
6 17,3 40,6 2,25   6

19,6

 31,5

1,90

  
7 16,9 33,6 2,13   7

11,5

 52,5

3,00

  
8 14,8 13,9 2,56   8

17,2

 37,0

2,22

  
9 19,6 32,5 1,90   9

19,5

 43,6

1,96

  
10 11,4 52,5 3,00   10

12,5

 48,3

2,82

  

Варіант 7

Варіант 8

  
№ з/п Вантажо-оборот Запаси Трудо-місткість   № з/п Вантажо-оборот

Запаси

Трудо-місткість
1 16,9 33,7 2,13   1 19,5

43,6

1,95
2 14,5 13,8 2,56   2 12,4

48,3

2,83
3 19,5 31,5 1,91   3 17,2

44,7

2,29
4 11,5 52,5 3,00   4 19,5

35,7

2,33
5 17,1 37,0 2,23   5 12,6

49,2

2,31
6 19,6 43,6 1,96   6 16,5

41,3

2,54
7 12,5 48,3 2,82   7 16,1

43,8

2,11
8 16,5 44,7 2,29   8 16,0

48,5

2,42
9 16,0 35,7 2,33   9 16,2

42,3

2,38
10 16,1 49,3 2,31   10 18,0

43,0

2,46

Варіант 9

Варіант 10

  
№ з/п Вантажо-оборот Запаси Трудо-місткість   № з/п Вантажо-оборот

Запаси

Трудо-місткість
1 11,7 44,2 2,85   1 18,4

38,7

1,89
2 18,3 42,4 1,81   2 15,6

36,5

2,25
3 18,2 38,9 1,88   3 17,5

35,2

1,98
4 15,6 36,4 2,25   4 13,8

45,5

2,48
5 17,4 35,2 1,98   5 15,0

35,2

2,25
6 13,8 45,5 2,48   6 18,7

41,6

1,85
7 15,0 35,2 2,25   7 16,2

42,2

2,15
8 18,6 41,6 1,85   8 15,7

40,4

2,25
9 16,2 42,2 2,15   9 17,9

47,3

1,90
10 15,7 40,4 2,25   10 15,4

47,1

2,20
                       

 

     

Варіант 11

Варіант 12
№ з/п Вантажо-оборот

Запаси

 Трудо-місткість

 

№

з/п

Вантажо-оборот

Запаси

Трудо-місткість

  
1 13,8

45,5

 2,46

 

1

18,8

42,1

1,86

  
2 15,0

35,2

 2,25

 

2

16,4

42,3

2,15

  
3 18,6

41,6

 1,85

 

3

16,1

40,4

2,25

  
4 16,2

42,3

 2,15

 

4

17,8

47,4

1,90

  
5 15,7

40,4

 2,25

 

5

15,5

47,1

2,20

  
6 17,9

47,4

 1,90

 

6

16,3

43,2

2,10

  
7 15,3

47,1

 2,20

 

7

17,8

39,0

1,86

  
8 16,3

43,2

 2,09

 

8

16,8

38,2

2,00

  
9 17,7

39,1

 1,87

 

9

17,5

37,3

2,48

  
10 16,8

38,2

 2,00

 

10

16,7

36,7

2,02

  

Варіант 13

Варіант 14

№ з/п Вантажо-оборот

Запаси

 Трудо-місткість

 

№

з/п

Вантажо-оборот

Запаси

Трудо-місткість

  
1 13,8

48,0

 2,45

 

1

16,8

40,4

1,88

  
2 14,8

46,4

 2,30

 

2

17,0

42,3

2,00

  
3 16,9

42,3

 2,00

 

3

14,8

40,1

2,21

  
4 16,8

39,4

 2,05

 

4

17,9

39,4

2,01

  
5 14,8

42,3

 2,23

 

5

16,9

39,1

2,31

  
6 18,0

40,1

 1,89

 

6

19,7

43,2

2,16

  
7 17,5

39,4

 2,00

 

7

14,0

44,5

1,74

  
8 15,7

39,1

 2,21

 

8

17,1

45,7

2,25

  
9 15,3

43,2

 2,01

 

9

18,2

37,8

1,87

  
10 14,9

44,7

 2,31

 

10

17,4

46,4

1,82

  

Варіант 15

Варіант 16

№ з/п Вантажо-оборот

Запаси

Трудо-місткість

 

№

з/п

Вантажо-оборот

Запаси

Трудо-місткість

1 19,7

37,8

1,74

 

1

32,1

48,0

2,12

2 14,0

46,4

2,25

 

2

31,0

42,1

2,20

3 17,2

48,2

1,88

 

3

32,4

42,3

2,11

4 18,3

49,6

1,82

 

4

33,4

43,7

2,08

5 17,4

46,4

1,90

 

5

31,2

42,8

2,21

6 16,1

42,6

1,98

 

6

34,8

41,8

1,88

7 18,8

49,4

1,77

 

7

35,4

30,8

1,91

8 17,9

40,1

1,89

 

8

33,0

44,4

2,00

9 17,6

39,4

2,00

 

9

34,8

51,2

1,90

10 15,7

39,1

2,21

 

10

33,3

54,6

1,99

                                     

Контрольні запитання й завдання

1. Яким чином вимірюють щільність зв’язку між змінними економетричної моделі?

2. Яку інформацію дають різні типи коефіцієнтів кореляції? Які властивості коефіцієнтів кореляції ви знаєте?

3. Розкрийте сутність стандартизації даних. Укажіть формули для розрахунку стандартизованих даних.

4. Наведіть формулу розрахунку кореляційної матриці.

5. Укажіть, як можна перевірити статистичну значущість коефіцієнта кореляції. Наведіть формулу для розрахункового значення критерію для перевірки значущості.

6. Поясніть зміст частинних коефіцієнтів кореляції. Наведіть два способи розрахунку частинних коефіцієнтів кореляції та відповідні формули.

Лабораторна робота 2
Економетрична модель із двома змінними: побудова і аналіз

Виконавши цю роботу, ви навчитеся:

· будувати парну лінійну економетричну модель;

· перевіряти статистичну значущість коефіцієнтів моделі;

· перевіряти статистичну значущість моделі;

· визначати точність моделі;

· аналізувати зв’язок між змінними за допомогою отриманого рівняння регресії та здійснювати прогнозування.

Ключові поняття: регресія; результативний фактор (ендогенна змінна); фактор-ознака (екзогенна змінна); стохастична складова регресії; коефіцієнт кореляції; специфікація моделі; метод найменших квадратів (МНК); система нормальних рівнянь; стандартна похибка параметрів моделі; статистична значущість оцінок параметрів моделі; t-критерій; довірчий інтервал; значущість економетричної моделі; F-критерій; залишкова дисперсія; коефіцієнт детермінації; інтервальний прогноз; точковий прогноз; похибка прогнозу.

Теоретичні відомості

Серед численних зв’язків між економічними показниками завжди можна виділити такий показник, вплив якого на результативну ознаку є основний, найбільш важливий. Щоб виміряти цей зв’язок кількісно, необхідно побудувати економетричну модель із двома змінними (просту модель).

Визначення. Економетричну модель, у рівняння якої включено лише одну пояснювальну змінну, називають парною. Загальний вигляд моделі такий:

Y = f (X, ε),

де Y – залежна змінна (результативна ознака); X – незалежна змінна (фактор);
ε – стохастична складова.

Постановка задачі. За даними n спостережень за спільною зміною двох параметрів х та у 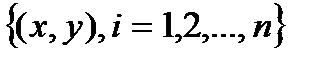 необхідно визначити аналітичну залежність 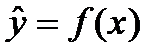, яка б щонайкраще описувала дані спостереження.

Розв’язування задачі побудови якісної математичної моделі у формі рівняння регресії на основі певної вибірки можна умовно поділити на такі три етапи:

1) специфікація моделі (вибір форми рівняння регресії);

2) оцінка параметрів, які є складовими частинами вибраного рівняння;

3) аналіз якості рівняння математичної моделі досліджуваного процесу та перевірка моделі на адекватність (відповідність емпіричним даним) із можливим наступним удосконаленням специфікації рівняння зв’язку.

Специфікація моделі

Парну регресію застосовують, якщо існує домінуючий фактор, який і виступає пояснювальною змінною. Аналітична форма моделі може бути різною залежно від економічної сутності зв’язків. Розглядають лінійні та нелінійні регресії.

Лінійну регресію описують рівнянням Y = a 0 + a 1 X. Нелінійні регресії поділяються на два класи (табл. 3):

· регресії, нелінійні відносно включених в аналіз пояснювальних  змінних, але лінійні за параметрами;

· регресії, нелінійні за параметрами.

 

                                                                                           Таблиця 3

Вид регресії Приклад

Регресії, лінійні за параметрами

Поліноми різних степенів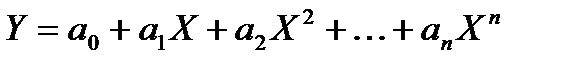
Рівностороння гіпербола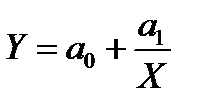

Регресії, нелінійні за параметрами
Степенева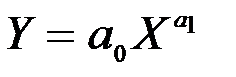
Показникова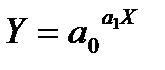
Експоненціальна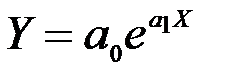

 

У випадку парної регресії вибір специфікації моделі можна виконати візуально, використовуючи графічне зображення емпіричних даних як точок (xi, yi) на кореляційному полі в декартовій системі координат, які утворюють так звану діаграму розсіювання (рис. 2, а – в). Так, виходячи з рис.2,а можна припустити, що зв’язок між Y та Х є лінійний: 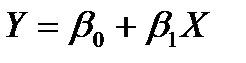; зображена на
рис.2,б залежність близька до параболічної: 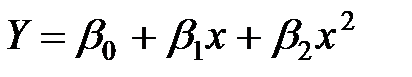; на рис.2,в явної залежності між Y та Х не спостерігаємо.

 

 

у                                    у                                      y

 


0                      х        0                      х         0                        х

        

а                                      б                                    в

Рис. 2. Діаграми розсіювання

⇐ Предыдущая12345678910Следующая ⇒
Поделиться с друзьями:

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...



© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!

0.393 с.