Для перевірки гіпотези Н0: r = 0 (коефіцієнт кореляції незначущий) і альтернативної їй гіпотези Н1: r ≠ 0 (коефіцієнт кореляції відмінний від нуля та значущий) підраховують статистичний критерій: 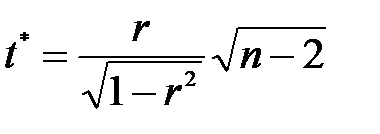 .
.
За заданим рівнем значущості a і степенями вільності 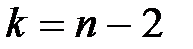 встановлюють критичне значення
встановлюють критичне значення 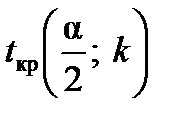 (таблиця розподілу Стьюдента) та порівнюють обчислене значення
(таблиця розподілу Стьюдента) та порівнюють обчислене значення 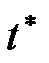 з табличним. На основі порівняння роблять висновок стосовно прийняття гіпотези.
з табличним. На основі порівняння роблять висновок стосовно прийняття гіпотези.
Правило прийняття рішення
1. Якщо 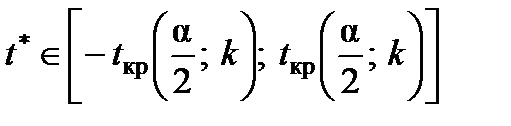 , то приймають гіпотезу Н0 про статистичну незначущість розрахованого коефіцієнта кореляції.
, то приймають гіпотезу Н0 про статистичну незначущість розрахованого коефіцієнта кореляції.
2. Якщо 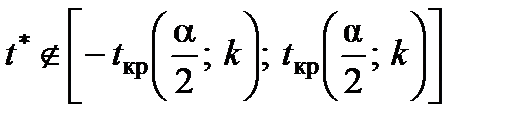 , то приймають гіпотезу Н1 про статистичну значущість коефіцієнта кореляції.
, то приймають гіпотезу Н1 про статистичну значущість коефіцієнта кореляції.
2. Перевірка статистичної значущості оцінок параметрів 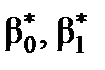 економетричної моделі
економетричної моделі
Для перевірки нульової гіпотези 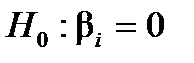 (коефіцієнт незначущий) за альтернативної гіпотези
(коефіцієнт незначущий) за альтернативної гіпотези 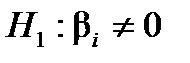 (коефіцієнт значущий) вибирають як статистичний критерій випадкову величину
(коефіцієнт значущий) вибирають як статистичний критерій випадкову величину 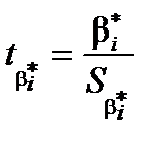 (
( 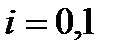 ), де
), де 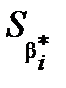 – стандартні похибки оцінок параметрів (дод. 1).
– стандартні похибки оцінок параметрів (дод. 1).
Для розрахунку 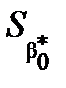 та
та 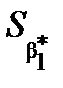 застосовують формули
застосовують формули
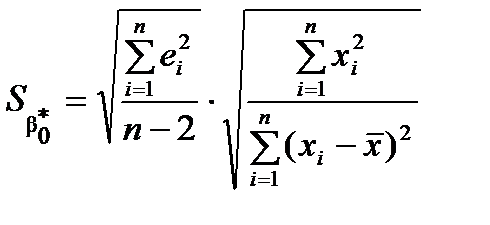 ,
, 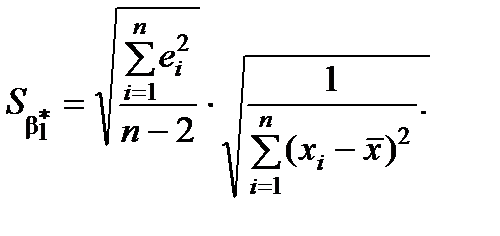
Далі знаходять критичне значення 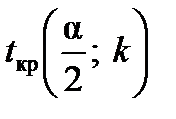 з t-розподілу Стьюдента із
з t-розподілу Стьюдента із 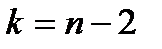 степенями вільності за обраним рівнем значущості a.
степенями вільності за обраним рівнем значущості a.
Правило прийняття рішення
1. Якщо 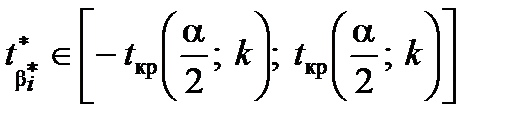 , то приймають гіпотезу Н0 про те,
, то приймають гіпотезу Н0 про те,
що 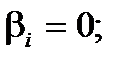
2. Якщо 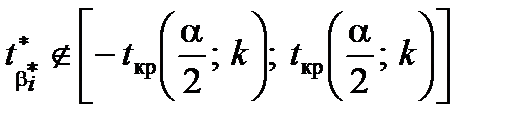 , то приймають гіпотезу
, то приймають гіпотезу 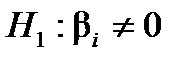 про значущість вибіркового коефіцієнта регресії.
про значущість вибіркового коефіцієнта регресії.
Зауваження.
1. Стандартні похибки характеризують середні лінійні коливання оцінок параметрів моделі навколо свого математичного сподівання. Чим менші ці похибки, тим більш стійкі оцінки параметрів.
2. Статистична значущість коефіцієнта 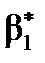 свідчить про істотний вплив на залежну змінну вибраної незалежної та дозволяє визначити модель як якісну.
свідчить про істотний вплив на залежну змінну вибраної незалежної та дозволяє визначити модель як якісну.
3. Статистична незначущість коефіцієнта 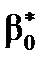 вказує на те, що всі інші фактори, які не були враховані в регресійній моделі, не роблять значного впливу на залежну змінну.
вказує на те, що всі інші фактори, які не були враховані в регресійній моделі, не роблять значного впливу на залежну змінну.
Поняття довірчого інтервалу параметрів регресії
Розраховані значення показників є наближені, отримані на основі вибіркових даних. Для оцінки того, наскільки точні значення показників можуть відрізнятися від розрахованих, для статистично значущих параметрів можна побудувати довірчий інтервал.
Визначення. Довірчий інтервал – це інтервал, у якому з певною ймовірністю можна очікувати фактичне значення досліджуваної величини.
Довірчі інтервали коефіцієнтів 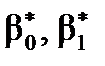 обчислюють за формулами
обчислюють за формулами
- для 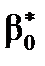 :
: 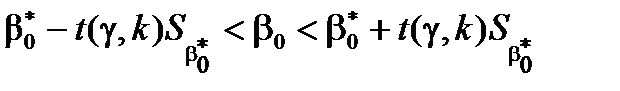 ;
;
- для 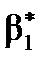 :
: 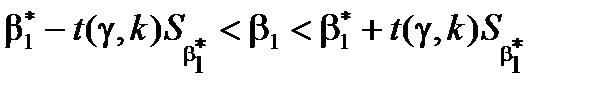 ,
,
де 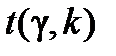 визначають згідно з таблицею розподілу Стьюдента за заданою надійністю g = 1-a і кількістю степенів вільності
визначають згідно з таблицею розподілу Стьюдента за заданою надійністю g = 1-a і кількістю степенів вільності 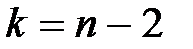 .
.





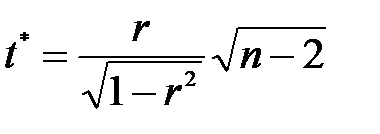 .
.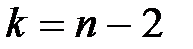 встановлюють критичне значення
встановлюють критичне значення 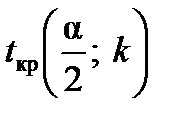 (таблиця розподілу Стьюдента) та порівнюють обчислене значення
(таблиця розподілу Стьюдента) та порівнюють обчислене значення 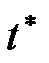 з табличним. На основі порівняння роблять висновок стосовно прийняття гіпотези.
з табличним. На основі порівняння роблять висновок стосовно прийняття гіпотези.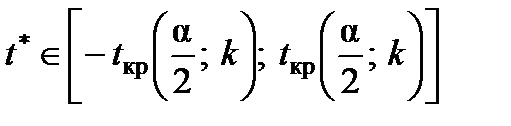 , то приймають гіпотезу Н0 про статистичну незначущість розрахованого коефіцієнта кореляції.
, то приймають гіпотезу Н0 про статистичну незначущість розрахованого коефіцієнта кореляції.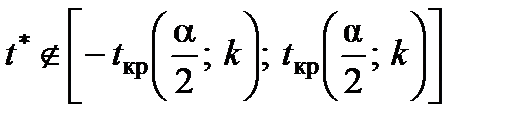 , то приймають гіпотезу Н1 про статистичну значущість коефіцієнта кореляції.
, то приймають гіпотезу Н1 про статистичну значущість коефіцієнта кореляції.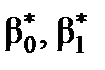 економетричної моделі
економетричної моделі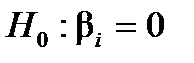 (коефіцієнт незначущий) за альтернативної гіпотези
(коефіцієнт незначущий) за альтернативної гіпотези 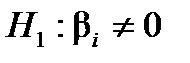 (коефіцієнт значущий) вибирають як статистичний критерій випадкову величину
(коефіцієнт значущий) вибирають як статистичний критерій випадкову величину 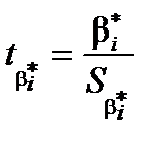 (
( 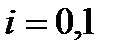 ), де
), де 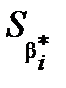 – стандартні похибки оцінок параметрів (дод. 1).
– стандартні похибки оцінок параметрів (дод. 1).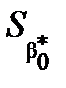 та
та 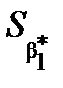 застосовують формули
застосовують формули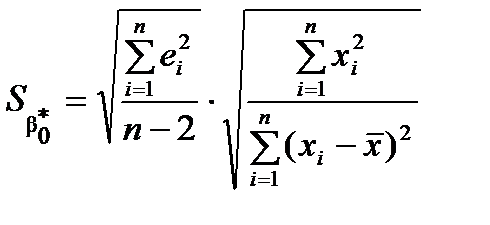 ,
, 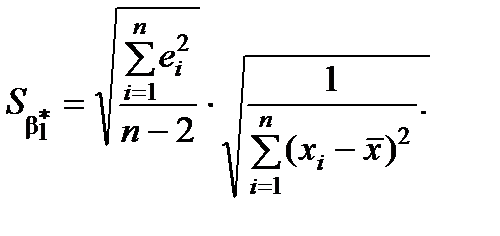
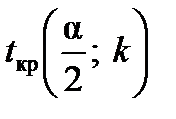 з t-розподілу Стьюдента із
з t-розподілу Стьюдента із 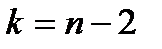 степенями вільності за обраним рівнем значущості a.
степенями вільності за обраним рівнем значущості a.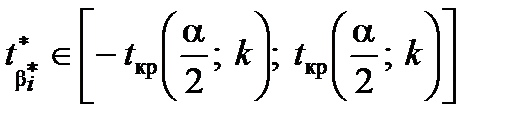 , то приймають гіпотезу Н0 про те,
, то приймають гіпотезу Н0 про те, 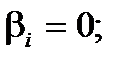
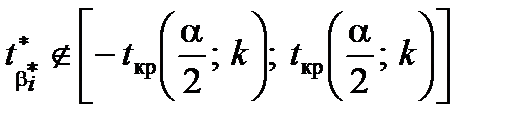 , то приймають гіпотезу
, то приймають гіпотезу 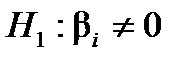 про значущість вибіркового коефіцієнта регресії.
про значущість вибіркового коефіцієнта регресії.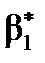 свідчить про істотний вплив на залежну змінну вибраної незалежної та дозволяє визначити модель як якісну.
свідчить про істотний вплив на залежну змінну вибраної незалежної та дозволяє визначити модель як якісну.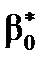 вказує на те, що всі інші фактори, які не були враховані в регресійній моделі, не роблять значного впливу на залежну змінну.
вказує на те, що всі інші фактори, які не були враховані в регресійній моделі, не роблять значного впливу на залежну змінну.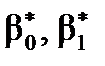 обчислюють за формулами
обчислюють за формулами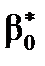 :
: 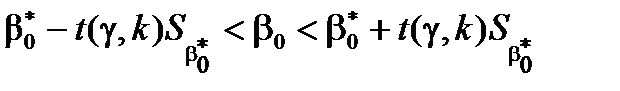 ;
;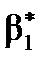 :
: 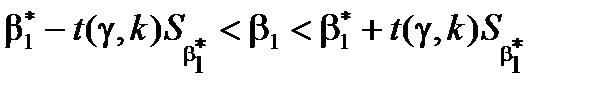 ,
,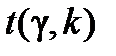 визначають згідно з таблицею розподілу Стьюдента за заданою надійністю g = 1-a і кількістю степенів вільності
визначають згідно з таблицею розподілу Стьюдента за заданою надійністю g = 1-a і кількістю степенів вільності 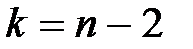 .
.


