Потрібно дослідити залежність обсягів реалізації продукції Y підприємства від його кредиторської заборгованості X протягом року на основі даних його фінансової звітності (табл. 5).
Таблиця 5
| Обсяг реалізації продукції Y, млн грн
| Кредиторська заборгованість X, млн грн
|
| 0,54
| 0,42
|
| 0,47
| 0,37
|
| 0,65
| 0,66
|
| 0,83
| 0,71
|
| 0,76
| 0,83
|
| 0,50
| 0,57
|
| 0,72
| 0,69
|
| 0,84
| 0,75
|
| 0,93
| 0,88
|
| 1,11
| 0,99
|
| 0,94
| 1,01
|
| 1,14
| 1,17
|
У ході роботи необхідно:
1) визначити вид зв’язку між заданими показниками;
2) розрахувати оцінки параметрів за допомогою МНК;
3) виконати аналіз якості побудованої моделі та оцінок її параметрів;
4) розрахувати прогнозне значення залежної змінної та довірчі інтервали прогнозу;
5) визначити коефіцієнт еластичності.
Розв’язування
1. Специфікація моделі
У цьому прикладі слід розглянути зв’язок між двома показниками – обсягом реалізації продукції та кредиторською заборгованістю підприємства, отже, маємо парну регресію. Позначимо залежну величину – обсяг реалізації продукції – буквою y, а незалежну величину– кредиторську заборгованість –
через х. Залежність між наведеними показниками зобразимо графічно у вигляді точкового графіку (рис. 5). Очевидно, що в цьому випадку зв’язок між розглядуваними показниками близький до лінійного. Емпіричне рівняння матиме вигляд
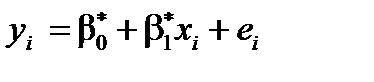 .
.
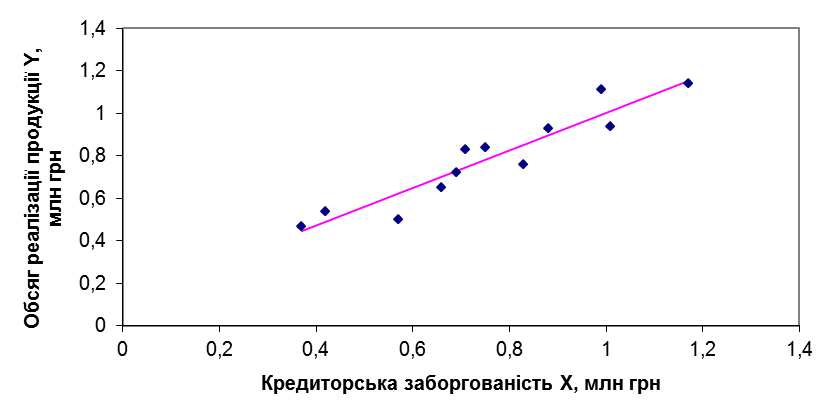
Рис. 5. Точковий графік залежності між змінними
2. Визначення параметрів вибраного рівняння
Розрахуємо значення коефіцієнтів за формулами
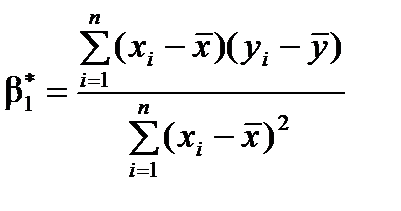 ,
, 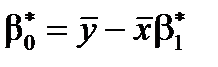 .
.
Для виконання потрібних обчислень слід поетапно розрахувати величини 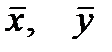 ,
, 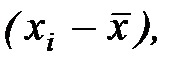
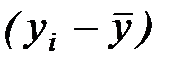 ,
, 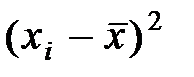 для кожного спостереження
для кожного спостереження 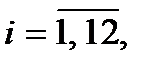 а також
а також 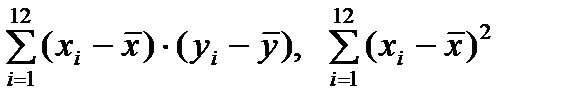 .
.
Обчислимо
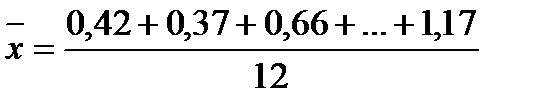 =0,7542,
=0,7542,
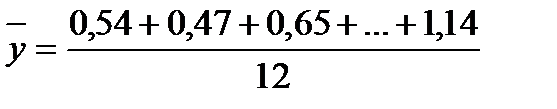 = 0,7858.
= 0,7858.
Розрахунки значень інших величин подано в табл. 6. На основі встановлених значень одержимо
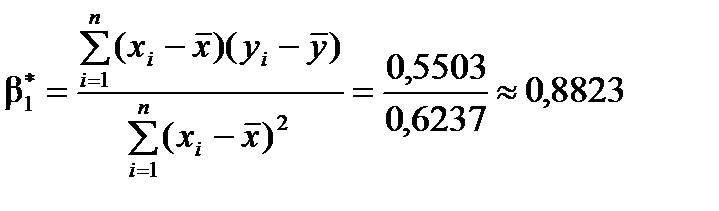 ,
, 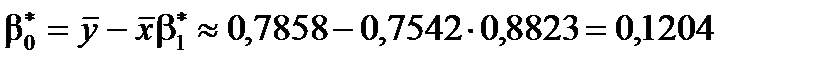 .
.
Отже, емпіричне лінійне рівняння парної регресії (економетрична модель залежності між обсягом реалізації продукції та кредиторською заборгованістю) за визначеними 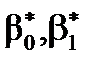 має вигляд
має вигляд 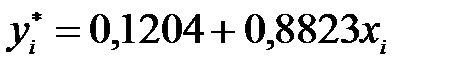 .
.
Таблиця 6
| Номер
спосте-реження
| 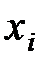
| 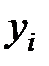
| 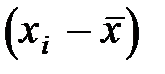
| 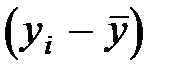
| 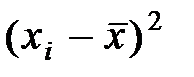
| 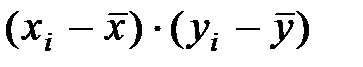
| 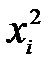
|
| 1
| 0,42
| 0,54
| -0,33
| -0,25
| 0,11
| 0,08
| 0,18
|
| 2
| 0,37
| 0,47
| -0,38
| -0,32
| 0,15
| 0,12
| 0,14
|
| 3
| 0,66
| 0,65
| -0,09
| -0,14
| 0,01
| 0,01
| 0,44
|
| 4
| 0,71
| 0,83
| -0,04
| 0,04
| 0,00
| 0,00
| 0,50
|
| 5
| 0,83
| 0,76
| 0,08
| -0,03
| 0,01
| 0,00
| 0,69
|
| 6
| 0,57
| 0,5
| -0,18
| -0,29
| 0,03
| 0,05
| 0,32
|
| 7
| 0,69
| 0,72
| -0,06
| -0,07
| 0,00
| 0,00
| 0,48
|
| 8
| 0,75
| 0,84
| 0,00
| 0,05
| 0,00
| 0,00
| 0,56
|
| 9
| 0,88
| 0,93
| 0,13
| 0,14
| 0,02
| 0,02
| 0,77
|
| 10
| 0,99
| 1,11
| 0,24
| 0,32
| 0,06
| 0,08
| 0,98
|
| 11
| 1,01
| 0,94
| 0,26
| 0,15
| 0,07
| 0,04
| 1,02
|
| 12
| 1,17
| 1,14
| 0,42
| 0,35
| 0,17
| 0,15
| 1,37
|
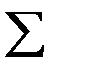
| 9,05
| 9,43
| 0,00
| 0,00
| 0,62
| 0,55
| 7,45
|
3. Аналіз якості моделі
3.1. Перевірка загальної якості рівняння регресії
Загальну якість рівняння регресії оцінюють, визначаючи коефіцієнт детермінації за формулою
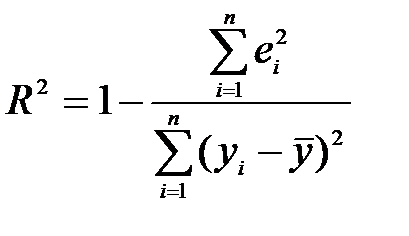 або
або 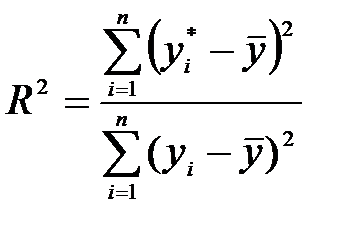 .
.
Обчислимо значення 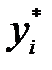 , відповідні значення
, відповідні значення 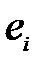 (розрахуємо їх як
(розрахуємо їх як 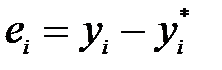 ), суми
), суми 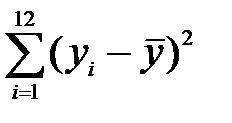 ,
, 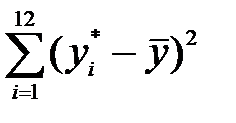 ,
, 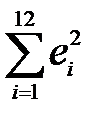 . Усі результати занесемо в табл. 7. На основі цих даних матимемо:
. Усі результати занесемо в табл. 7. На основі цих даних матимемо:
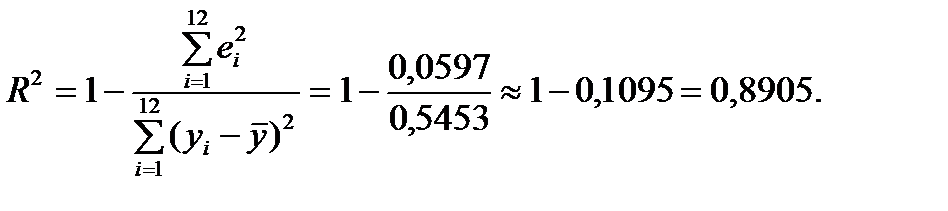
Відомо, що 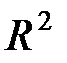 дозволяє визначити, наскільки добре емпіричне рівняння регресії узгоджується зі статистичними даними, тобто наскільки реальні значення відхиляються від побудованої лінії регресії. Для розглядуваного прикладу з рис. 5 можна побачити, що точки, відповідні реальним спостереженням, розташовані дуже близько від лінії регресії, отже, отриманий результат
дозволяє визначити, наскільки добре емпіричне рівняння регресії узгоджується зі статистичними даними, тобто наскільки реальні значення відхиляються від побудованої лінії регресії. Для розглядуваного прикладу з рис. 5 можна побачити, що точки, відповідні реальним спостереженням, розташовані дуже близько від лінії регресії, отже, отриманий результат 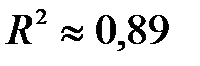 є цілком закономірний. Зробимо висновок: на 89% зміна обсягів реалізації продукції визначена зміною кредиторської заборгованості підприємства і лише на 11% такі зміни пов’язані з іншими (не врахованими в даній економетричній моделі) факторами.
є цілком закономірний. Зробимо висновок: на 89% зміна обсягів реалізації продукції визначена зміною кредиторської заборгованості підприємства і лише на 11% такі зміни пов’язані з іншими (не врахованими в даній економетричній моделі) факторами.
Таблиця 7
| Номер
спостереження
| 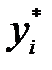
| 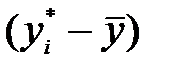
| 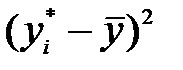
| 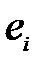
| 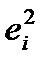
| 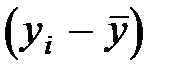
| 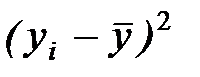
|
| 1
| 0,4910
| -0,2948
| 0,0869
| 0,0490
| 0,0024
| -0,2458
| 0,0604
|
| 2
| 0,4469
| -0,3390
| 0,1149
| 0,0231
| 0,0005
| -0,3158
| 0,0998
|
| 3
| 0,7027
| -0,0831
| 0,0069
| -0,0527
| 0,0028
| -0,1358
| 0,0185
|
| 4
| 0,7469
| -0,0390
| 0,0015
| 0,0831
| 0,0069
| 0,0442
| 0,0020
|
| 5
| 0,8527
| 0,0669
| 0,0045
| -0,0927
| 0,0086
| -0,0258
| 0,0007
|
| 6
| 0,6233
| -0,1625
| 0,0264
| -0,1233
| 0,0152
| -0,2858
| 0,0817
|
| 7
| 0,7292
| -0,0566
| 0,0032
| -0,0092
| 0,0001
| -0,0658
| 0,0043
|
| 8
| 0,7822
| -0,0037
| 0,0000
| 0,0578
| 0,0033
| 0,0542
| 0,0029
|
| 9
| 0,8969
| 0,1110
| 0,0123
| 0,0331
| 0,0011
| 0,1442
| 0,0208
|
| 10
| 0,9939
| 0,2081
| 0,0433
| 0,1161
| 0,0135
| 0,3242
| 0,1051
|
| 11
| 1,0116
| 0,2257
| 0,0510
| -0,0716
| 0,0051
| 0,1542
| 0,0238
|
| 12
| 1,1527
| 0,3669
| 0,1346
| -0,0127
| 0,0002
| 0,3542
| 0,1254
|
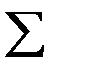
| 9,4300
| 0,0000
| 0,4856
| 0,0000
| 0,0597
| 0,0000
| 0,5453
|
Оскільки 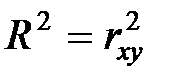 , обчислимо значення парного коефіцієнта кореляції
, обчислимо значення парного коефіцієнта кореляції 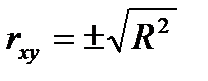 та перевіримо його статистичну значущість. Матимемо
та перевіримо його статистичну значущість. Матимемо 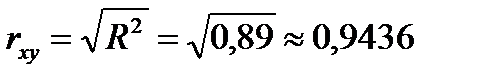 . Коефіцієнт кореляції є додатний, оскільки маємо пряму залежність між змінними х та у, що видно з рис.5.
. Коефіцієнт кореляції є додатний, оскільки маємо пряму залежність між змінними х та у, що видно з рис.5.
Для перевірки статистичної значущості r виберемо статистичний критерій 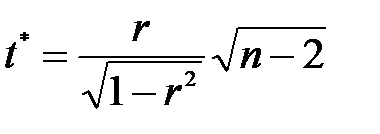 . Обчислене значення
. Обчислене значення 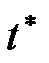 порівняємо з табличним значенням, вибраним за заданим рівнем значущості a і степенями вільності
порівняємо з табличним значенням, вибраним за заданим рівнем значущості a і степенями вільності 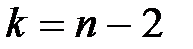 , на основі чого зробимо висновок стосовно прийняття гіпотези про значущість (незначущість) коефіцієнта кореляції:
, на основі чого зробимо висновок стосовно прийняття гіпотези про значущість (незначущість) коефіцієнта кореляції:
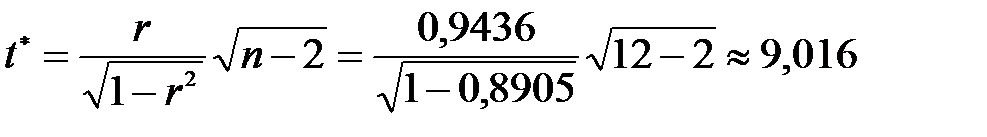 .
.
Якщо a = 0,05, 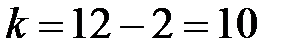 , то табличне значення
, то табличне значення
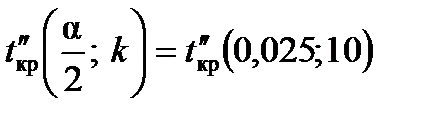 = 2,228;
= 2,228; 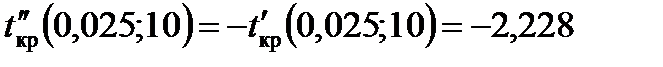 .
.
Оскільки 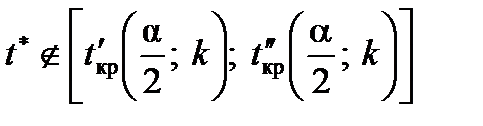 , приймемо гіпотезу про статистичну значущість розрахованого для розглядуваного прикладу коефіцієнта кореляції.
, приймемо гіпотезу про статистичну значущість розрахованого для розглядуваного прикладу коефіцієнта кореляції.
Загалом проведений аналіз якості побудованої лінії регресії дає підстави вважати дану модель якісною, а тому її можна застосовувати для подальших досліджень.
3.2. Перевірка статистичної значущості оцінок параметрів 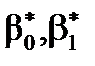 економетричної моделі
економетричної моделі
Для перевірки нульової гіпотези 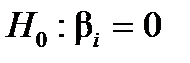 за альтернативної гіпотези
за альтернативної гіпотези 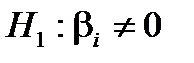 виберемо як статистичний критерій випадкову величину
виберемо як статистичний критерій випадкову величину
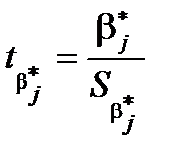 (
( 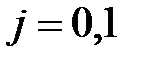 ).
).
Для розрахунку 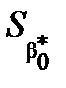 та
та 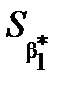 застосуємо формули
застосуємо формули
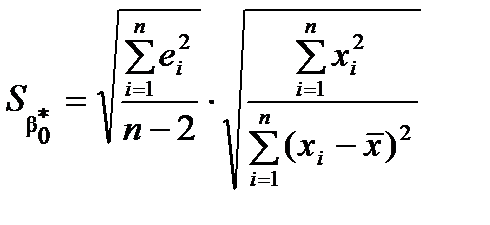 ,
, 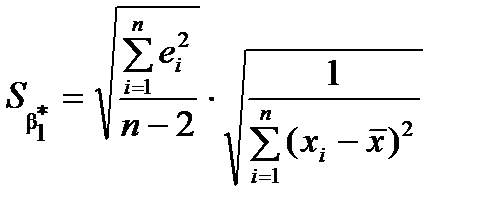 .
.
Обчислимо 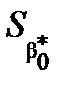 :
:
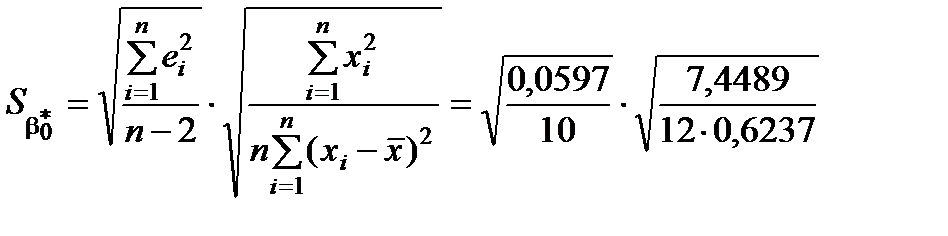

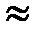 0,0773 × 0,99763
0,0773 × 0,99763 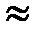 0,0771.
0,0771.
Визначимо 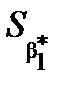 :
:
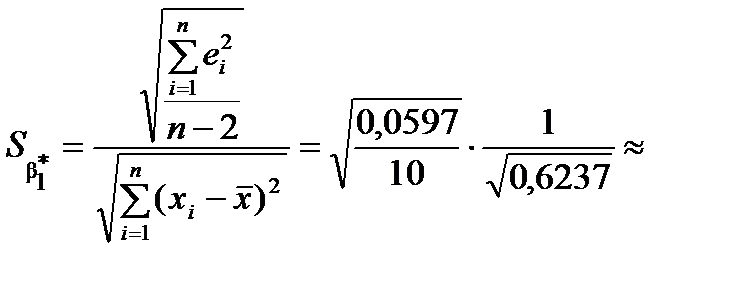 0,0773 × 1,2662
0,0773 × 1,2662 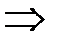
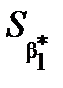
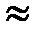 0,09786.
0,09786.
Тепер обчислимо спостережене значення вибраного статистичного критерію для кожного коефіцієнта:
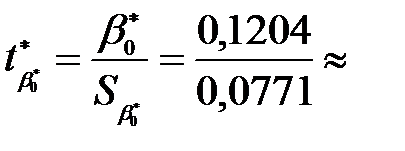 1,56 ,
1,56 , 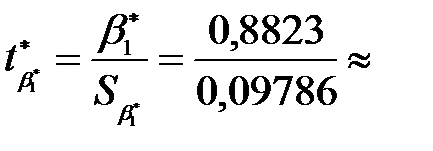 9,016.
9,016.
Як відомо, розраховані t-статистики мають розподіл Стьюдента (t-розподіл) із 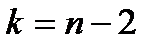 степенями вільності.
степенями вільності.
За вибраного рівня значущості 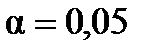 та кількості степенів вільності
та кількості степенів вільності 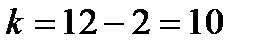 матимемо таке:
матимемо таке:
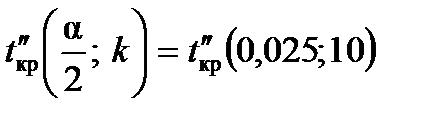 = 2,228,
= 2,228, 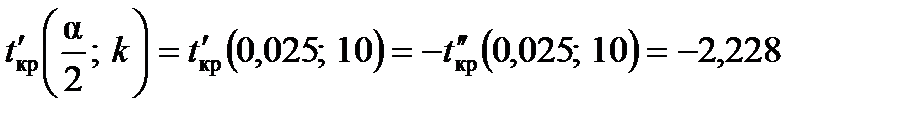 .
.
Нагадаємо, що коли 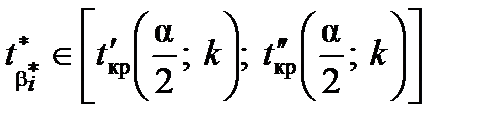 , слід прийняти гіпотезу про те, що
, слід прийняти гіпотезу про те, що 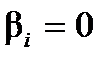 , і, навпаки,
, і, навпаки, 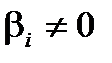 (
( 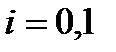 ), якщо
), якщо 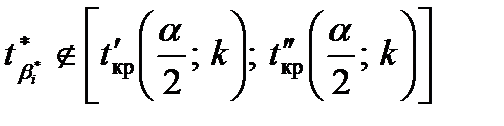 . Тобто область прийняття гіпотези, за якою
. Тобто область прийняття гіпотези, за якою 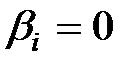 , визначена інтервалом
, визначена інтервалом
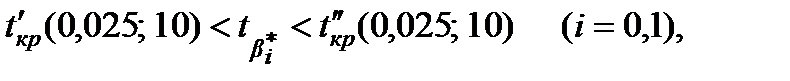
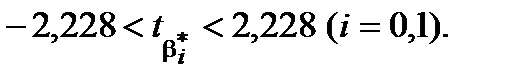
Отже, матимемо
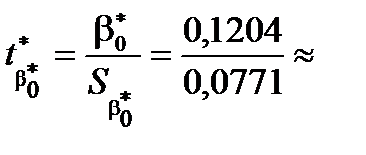 1,56
1,56 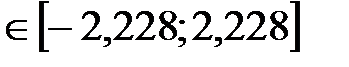 .
.
Таким чином, для оцінки параметра 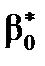 приймемо гіпотезу
приймемо гіпотезу 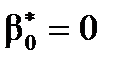 .
.
Статистична незначущість коефіцієнта 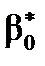 вказує на те, що всі інші фактори, не враховані в розглядуваній регресійній моделі, не роблять значного впливу на залежну змінну.
вказує на те, що всі інші фактори, не враховані в розглядуваній регресійній моделі, не роблять значного впливу на залежну змінну.
Аналогічно перевіримо статистичну значущість параметра 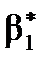 :
:
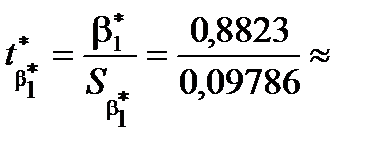 9,016
9,016 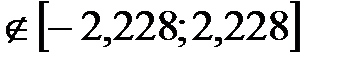 .
.
Як бачимо, оцінка параметра 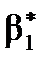 є статистично значуща, що свідчить про істотний вплив на залежну змінну вибраної незалежної.
є статистично значуща, що свідчить про істотний вплив на залежну змінну вибраної незалежної.
Отже, на цьому етапі аналізу побудованої економетричної моделі (перевірка статистичної значущості оцінок параметрів 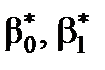 ) можна визначити модель як якісну, оскільки статистично значуща оцінка параметра
) можна визначити модель як якісну, оскільки статистично значуща оцінка параметра 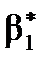 вказує на значний вплив вибраного фактора на залежну змінну, тоді як усі інші невраховані фактори (статистично незначуща оцінка параметра
вказує на значний вплив вибраного фактора на залежну змінну, тоді як усі інші невраховані фактори (статистично незначуща оцінка параметра 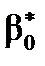 ) не впливають істотно на зміну значень y.
) не впливають істотно на зміну значень y.
3.3. Визначення довірчих інтервалів для оцінок параметрів 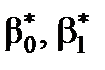 економетричної моделі
економетричної моделі
Довірчі інтервали обчислимо за такими формулами:
- для 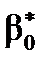 :
: 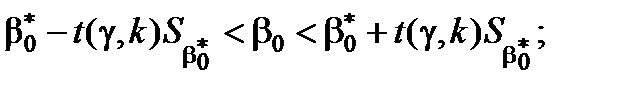
- для 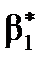 :
: 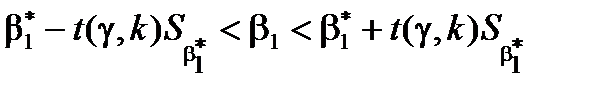 ,
,
де 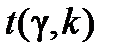 визначимо за допомогою таблиці за заданою надійністю g = 1-a і кількістю степенів вільності
визначимо за допомогою таблиці за заданою надійністю g = 1-a і кількістю степенів вільності 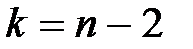 .
.
Виберемо рівень надійності 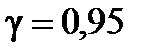 та, враховуючи, що кількість степенів вільності дорівнює
та, враховуючи, що кількість степенів вільності дорівнює 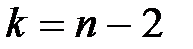 = 12 – 2 = 10, отримаємо
= 12 – 2 = 10, отримаємо 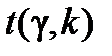 = 2,228. Отже, довірчі інтервали для оцінок параметрів визначені такими межами:
= 2,228. Отже, довірчі інтервали для оцінок параметрів визначені такими межами:
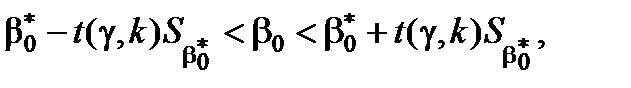
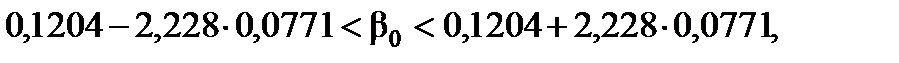
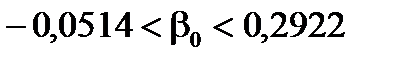 ,
,
аналогічно для 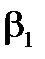 матимемо
матимемо
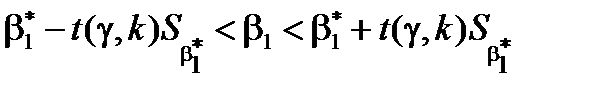 ,
,
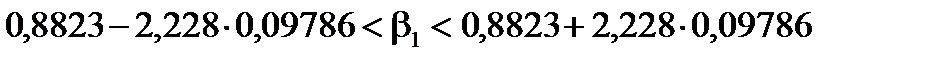 ,
,
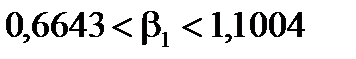 .
.
4. Прогнозування значень залежної змінної
Здійснимо прогноз обсягів реалізації продукції на наступний період часу залежно від кредиторської заборгованості, яка в січні наступного року запланована на рівні 1,25 млн. грн. Скористаємося визначеною залежністю між зазначеними показниками:
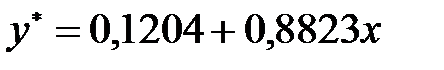 .
.
Найбільш грубою оцінкою такого прогнозу буде визначення однієї точки 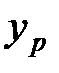 для значення
для значення 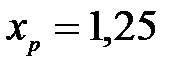 (точковий прогноз):
(точковий прогноз):
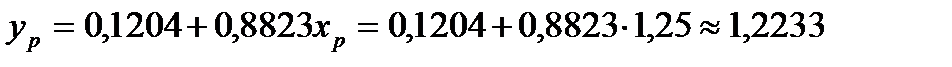
Зобразимо прогнозовані результати поряд із реальними значеннями спостережень (рис.6).
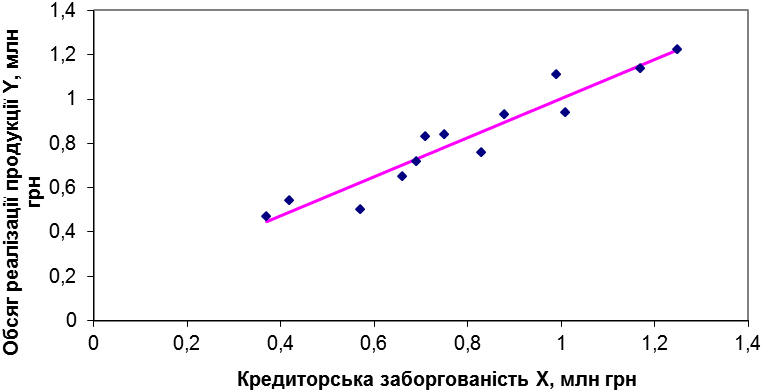
Рис. 6. Точковий графік залежності і прогнозне значення
Розрахована точка з координатами ( 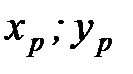 ) знаходиться на побудованій прямій, однак зрозуміло, що реальне значення
) знаходиться на побудованій прямій, однак зрозуміло, що реальне значення 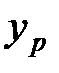 для вибраного
для вибраного 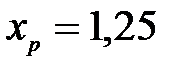 може відхилятися від лінії регресії, тому для розрахунку точних прогнозів визначають не одну точку, а прогнозний інтервал.
може відхилятися від лінії регресії, тому для розрахунку точних прогнозів визначають не одну точку, а прогнозний інтервал.
Розрахуємо інтервали для прогнозу:
– середнього значення залежної змінної;
– індивідуального значення залежної змінної.
4.1. Прогнозування середнього значення залежної змінної
Довірчий інтервал для теоретичної функції регресії знайдемо за формулою
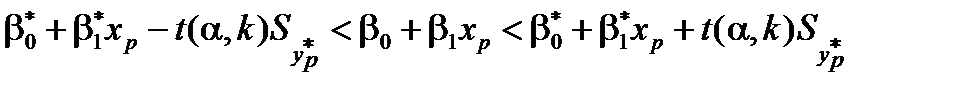 ,
,
де 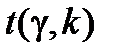 визначимо з допомогою таблиці за заданою надійністю
визначимо з допомогою таблиці за заданою надійністю 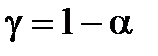 і кількістю степенів вільності
і кількістю степенів вільності 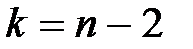 ;
; 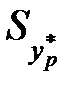 – похибка прогнозу, яку визначимо так:
– похибка прогнозу, яку визначимо так:
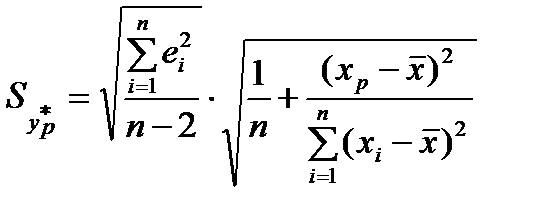 .
.
Обчислимо похибку прогнозу для середнього значення 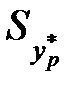 :
:
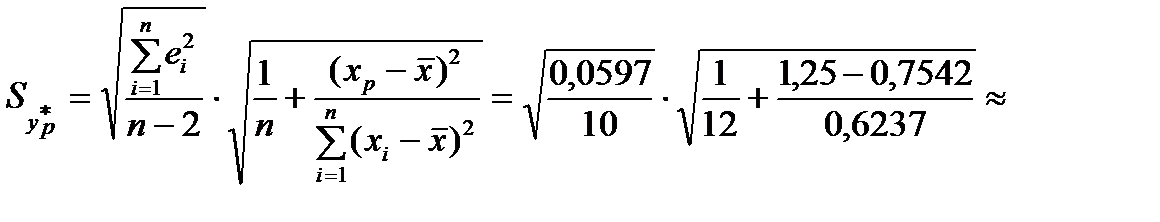

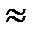 0,0773×0,937193
0,0773×0,937193 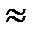 0,07243.
0,07243.
Значення 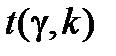 розрахуємо, як і в попередніх випадках, для
розрахуємо, як і в попередніх випадках, для 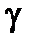 = 0,95 і кількості степенів вільності
= 0,95 і кількості степенів вільності 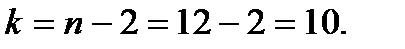 Матимемо
Матимемо 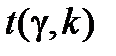 = 2,228. Таким чином,
= 2,228. Таким чином,
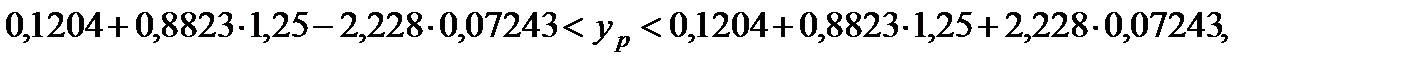
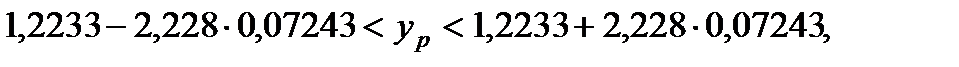
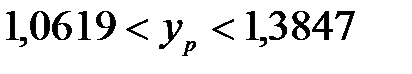 .
.
Тобто середнє значення обсягу реалізації продукції з імовірністю 0,95 буде знаходитися у визначених межах.
4.2. Прогнозування індивідуального значення залежної змінної
Знайдемо довірчий інтервал для прогнозованого індивідуального значення 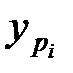 із заданою надійністю
із заданою надійністю 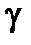 :
:
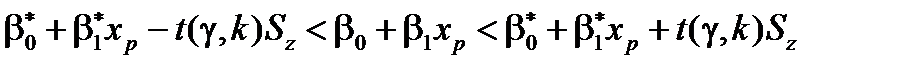 ,
,
де
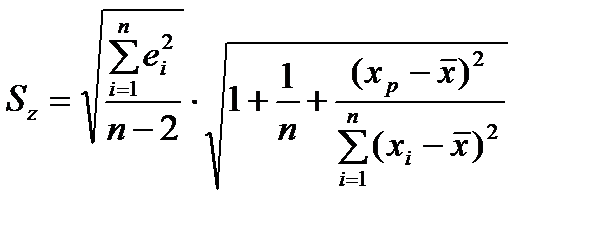 .
.
Розрахуємо 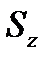 :
:
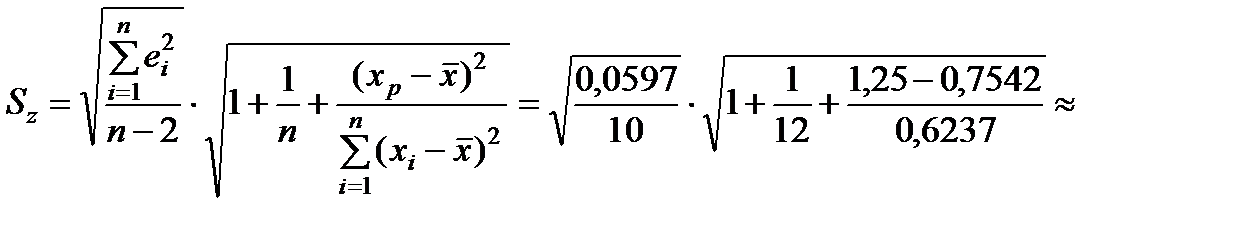

 1,484
1,484  0,1147.
0,1147.
Як і в попередніх випадках, 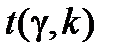 = 2,228 (для
= 2,228 (для 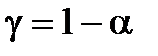 = 0,95 і кількості степенів вільності k = 10). Таким чином, межі прогнозного інтервалу складатимуть
= 0,95 і кількості степенів вільності k = 10). Таким чином, межі прогнозного інтервалу складатимуть
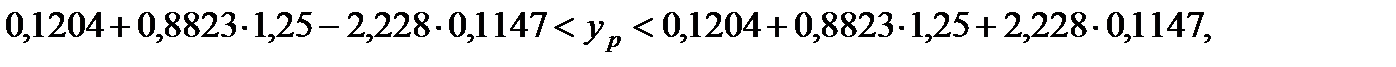
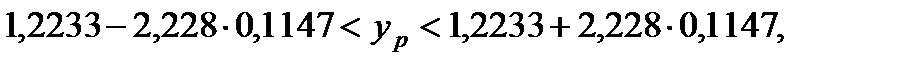
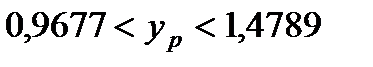 .
.
Тобто значення залежної змінної (обсяг реалізації продукції) з імовірністю 0,95 буде належати визначеному проміжку.
Зауважимо, що прогнозний інтервал для індивідуального значення ширший, ніж для середнього значення змінної.
5. Визначення коефіцієнта еластичності
Для парної лінійної регресії коефіцієнт еластичності визначимо таким чином: 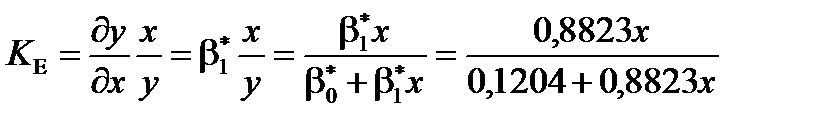 .
.

Використовуючи початкові значення 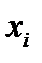 , коефіцієнт еластичності можна зобразити графічно (рис. 7).
, коефіцієнт еластичності можна зобразити графічно (рис. 7).
Рис.7. Графік еластичності моделі
У розглядуваному випадку 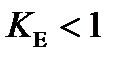 , тобто за зміни кредиторської заборгованості на 1% обсяг реалізації продукції змінюється менше ніж на 1%.
, тобто за зміни кредиторської заборгованості на 1% обсяг реалізації продукції змінюється менше ніж на 1%.
Зауваження. Під час виконання розрахунків можна застосувати статистичні й матричні функції електронних таблиць (дод. 2). Для знаходження параметрів моделі й оцінки її якості можна використати засоби пакета аналізу електронних
таблиць (дод. 3).
Завдання для самостійної роботи
Побудувати дві економетричні моделі, що характеризують:
а) залежність між витратами обігу та обсягом вантажообороту;
б) залежність між витратами обігу та фондомісткістю.
Побудову моделей виконати в такому порядку:
1) визначити вид зв’язку між заданими показниками;
2) розрахувати оцінки параметрів за допомогою МНК для лінійної моделі;
3) виконати аналіз якості побудованої моделі та оцінок її параметрів;
4) розрахувати прогнозне значення залежної змінної;
5) розрахувати довірчі інтервали прогнозу;
6) визначити коефіцієнт еластичності.
Варіант 1
|
|
Варіант 2
| |
| №
з/п
| Витрати
| Вантажо-оборот
| Фондо-місткість
|
| №
з/п
| Витрати
| Вантажо-оборот
| Фондо-місткість
| |
| 1
| 2,72
| 15,6
| 106,3
|
| 1
| 2,58
| 15,1
| 120,0
| |
| 2
| 3,04
| 13,5
| 128,5
|
| 2
| 2,64
| 16,1
| 118,4
| |
| 3
| 2,84
| 15,3
| 118,0
|
| 3
| 2,52
| 16,7
| 108,4
| |
| 4
| 2,89
| 14,9
| 121,2
|
| 4
| 2,75
| 15,4
| 110,0
| |
| 5
| 2,58
| 15,1
| 120,0
|
| 5
| 2,63
| 17,1
| 105,9
| |
| 6
| 2,64
| 16,1
| 118,4
|
| 6
| 2,48
| 16,8
| 117,7
| |
| 7
| 2,52
| 16,7
| 108,4
|
| 7
| 2,62
| 16,9
| 97,5
| |
| 8
| 2,75
| 15,4
| 110,0
|
| 8
| 2,88
| 16,1
| 113,7
| |
| 9
| 2,63
| 17,1
| 105,9
|
| 9
| 2,68
| 15,0
| 122,3
| |
|
Варіант 3
|
|
Варіант 4
|
| №
з/п
| Витрати
| Вантажо-оборот
| Фондомісткість
|
| №
з/п
| Витрати
| Вантажо-оборот
| Фондомісткість
|
| 1
| 2,48
| 16,8
| 117,7
|
| 1
| 2,75
| 16,8
| 110,0
|
| 2
| 2,62
| 16,9
| 97,5
|
| 2
| 2,63
| 15,5
| 105,9
|
| 3
| 2,88
| 16,1
| 113,7
|
| 3
| 2,48
| 17,0
| 117,7
|
| 4
| 2,68
| 15,0
| 122,3
|
| 4
| 2,62
| 16,8
| 97,5
|
| 5
| 2,52
| 18,0
| 102,0
|
| 5
| 2,88
| 16,9
| 113,7
|
| 6
| 2,74
| 17,2
| 106,7
|
| 6
| 2,68
| 16,1
| 122,3
|
| 7
| 2,56
| 17,1
| 108,5
|
| 7
| 2,56
| 15,0
| 102,0
|
| 8
| 2,68
| 16,4
| 114,3
|
| 8
| 2,74
| 18,0
| 106,7
|
| 9
| 2,55
| 16,7
| 94,3
|
| 9
| 2,60
| 17,2
| 108,5
|
| | | | | | | | | | | | | | | | | |
|
Варіант 5
|
|
Варіант 6
|
| №
з/п
| Витрати
| Вантажо-оборот
| Фондомісткість
|
| №
з/п
| Витрати
| Вантажо-оборот
| Фондомісткість
| |
| 1
| 2,92
| 14,1
| 87,8
|
| 1
| 2,45
| 17,1
| 71,3
| |
| 2
| 2,64
| 17,2
| 72,0
|
| 2
| 2,38
| 19,5
| 61,7
| |
| 3
| 2,79
| 17,1
| 72,4
|
| 3
| 3,04
| 12,5
| 96,2
| |
| 4
| 2,67
| 17,8
| 69,5
|
| 4
| 2,67
| 16,5
| 72,9
| |
| 5
| 2,68
| 16,2
| 75,0
|
| 5
| 2,70
| 16,0
| 75,0
| |
| 6
| 2,85
| 17,2
| 70,6
|
| 6
| 2,65
| 16,1
| 74,6
| |
| 7
| 2,40
| 16,8
| 73,4
|
| 7
| 2,79
| 16,2
| 74,1
| |
| 8
| 2,91
| 14,8
| 80,7
|
| 8
| 2,49
| 18,0
| 66,9
| |
| 9
| 2,29
| 19,6
| 62,2
|
| 9
| 3,27
| 11,4
| 98,6
| |
Варіант 7
|
|
Варіант 8
|
| №
з/п
| Витрати
| Вантажо-оборот
| Фондо-місткість
|
| №
з/п
| Витрати
| Вантажо-оборот
| Фондо-місткість
|
| 1
| 2,85
| 17,2
| 70,6
|
| 1
| 2,93
| 18,1
| 71,2
|
| 2
| 2,40
| 16,8
| 73,4
|
| 2
| 2,50
| 17,2
| 73,4
|
| 3
| 2,91
| 14,8
| 80,7
|
| 3
| 2,95
| 14,9
| 81,2
|
| 4
| 2,29
| 19,6
| 62,2
|
| 4
| 2,39
| 20,1
| 63,7
|
| 5
| 3,27
| 11,4
| 98,6
|
| 5
| 3,25
| 11,4
| 96,6
|
| 6
| 2,45
| 17,1
| 71,3
|
| 6
| 2,65
| 17,1
| 72,2
|
| 7
| 2,38
| 19,5
| 61,7
|
| 7
| 2,42
| 19,5
| 61,7
|
| 8
| 3,04
| 12,5
| 96,2
|
| 8
| 3,14
| 17,5
| 96,2
|
| 9
| 2,67
| 16,5
| 72,9
|
| 9
| 2,75
| 16,7
| 72,9
|
Варіант 9
|
|
Варіант 10
|
| №
з/п
| Витрати
| Вантажо-оборот
| Фондо-місткість
|
| №
з/п
| Витрати
| Вантажо-оборот
| Фондо-місткість
|
| 1
| 2,14
| 17,4
| 80,3
|
| 1
| 2,67
| 15,0
| 94,0
|
| 2
| 2,94
| 13,8
| 102,5
|
| 2
| 2,45
| 18,6
| 78,0
|
| 3
| 2,67
| 15,0
| 94,3
|
| 3
| 2,86
| 16,2
| 87,5
|
| 4
| 2,44
| 18,6
| 76,0
|
| 4
| 2,90
| 15,7
| 90,2
|
| 5
| 2,83
| 16,2
| 87,3
|
| 5
| 2,60
| 17,9
| 84,8
|
| 6
| 2,92
| 15,7
| 90,1
|
| 6
| 2,72
| 16,3
| 95,9
|
| 7
| 2,61
| 17,9
| 82,8
|
| 7
| 2,68
| 17,7
| 91,0
|
| 8
| 2,72
| 15,3
| 96,9
|
| 8
| 2,50
| 16,8
| 84,7
|
| 9
| 2,68
| 16,3
| 83,7
|
| 9
| 2,74
| 17,5
| 88,2
|
| | | | | | | | | | | | | |
Варіант 11
|
|
Варіант 12
|
| №
з/п
| Витрати
| Вантажо-оборот
| Фондо-місткість
|
| №
з/п
| Витрати
| Вантажо-оборот
| Фондо-місткість
|
| 1
| 2,83
| 13,8
| 68,0
|
| 1
| 2,69
| 14,9
| 69,4
|
| 2
| 2,75
| 14,8
| 64,3
|
| 2
| 2,48
| 16,1
| 58,7
|
| 3
| 2,40
| 16,9
| 55,1
|
| 3
| 2,11
| 19,7
| 62,3
|
| 4
| 2,30
| 16,8
| 55,5
|
| 4
| 2,82
| 14,0
| 83,8
|
| 5
| 2,47
| 14,8
| 63,3
|
| 5
| 2,43
| 17,1
| 68,5
|
| 6
| 2,45
| 17,9
| 52,7
|
| 6
| 2,34
| 18,2
| 64,5
|
| 7
| 2,48
| 17,6
| 53,7
|
| 7
| 2,48
| 17,4
| 67,6
|
| 8
| 2,41
| 15,7
| 60,2
|
| 8
| 2,69
| 16,1
| 72,9
|
| 9
| 2,34
| 15,2
| 62,2
|
| 9
| 2,36
| 18,8
| 62,4
|
Варіант 13
|
|
Варіант 14
|
| №
з/п
| Витрати
| Вантажо-оборот
| Фондо-місткість
|
| №
з/п
| Витрати
| Вантажо-оборот
| Фондо-місткість
|
| 1
| 2,35
| 16,8
| 56,5
|
| 1
| 2,46
| 19,0
| 65,4
|
| 2
| 2,48
| 15,0
| 64,3
|
| 2
| 2,70
| 16,3
| 73,9
|
| 3
| 2,45
| 17,5
| 53,7
|
| 3
| 2,58
| 17,5
| 68,5
|
| 4
| 2,47
| 17,6
| 54,7
|
| 4
| 2,34
| 18,4
| 64,5
|
| 5
| 2,42
| 15,7
| 60,2
|
| 5
| 2,43
| 17,2
| 69,3
|
| 6
| 2,34
| 15,2
| 62,4
|
| 6
| 2,84
| 15,0
| 83,8
|
| 7
| 2,70
| 14,9
| 69,5
|
| 7
| 2,15
| 19,8
| 62,3
|
| 8
| 2,48
| 16,1
| 58,7
|
| 8
| 2,49
| 16,1
| 58,7
|
| 9
| 2,15
| 19,7
| 62,3
|
| 9
| 2,60
| 14,9
| 69,4
|
|
Варіант 15
|
|
Варіант 16
|
| №
з/п
| Витрати
| Вантажо-оборот
| Фондо-місткість
|
| №
з/п
| Витрати
| Вантажо-оборот
| Фондо-місткість
|
| 1
| 2,27
| 32,1
| 112,5
|
| 1
| 2,17
| 33,3
| 109,4
|
| 2
| 1,94
| 31,0
| 116,4
|
| 2
| 1,80
| 36,1
| 101,1
|
| 3
| 2,32
| 32,4
| 111,6
|
| 3
| 2,36
| 38,3
| 102,6
|
| 4
| 2,49
| 33,2
| 108,9
|
| 4
| 2,50
| 30,6
| 128,5
|
| 5
| 2,57
| 31,2
| 116,5
|
| 5
| 2,27
| 32,1
| 122,5
|
| 6
| 2,01
| 34,8
| 104,5
|
| 6
| 2,33
| 37,6
| 105,2
|
| 7
| 1,87
| 35,4
| 102,7
|
| 7
| 2,51
| 34,8
| 114,8
|
| 8
| 2,39
| 33,0
| 110,2
|
| 8
| 2,40
| 34,2
| 116,0
|
| 9
| 2,18
| 34,8
| 104,7
|
| 9
| 2,50
| 34,2
| 116,0
|
| | | | | | | | | | |
Контрольні запитання й завдання
1. Які завдання виконують у ході побудови моделі регресії?
2. Дайте визначення парної регресії.
3. Які функції найчастіше застосовують для побудови моделі парної регресії?
4. Який вигляд має система нормальних рівнянь МНК у разі лінійної регресії?
5. За якою формулою обчислюють лінійний коефіцієнт парної
кореляції r?
6. Як визначають коефіцієнт детермінації? Що він показує?
7. Яким чином перевіряють значущість рівняння регресії й окремих коефіцієнтів?
8. Як будують довірчий інтервал прогнозу в разі лінійної регресії?
9. Що показують коефіцієнт еластичності, середній коефіцієнт еластичності? Як їх обчислюють?
Лабораторна робота 3
Загальна лінійна економетрична модель: побудова і аналіз
Виконавши цю роботу, ви навчитеся:
· оцінювати параметри множинної лінійної моделі за допомогою МНК;
· проводити верифікацію моделі множинної регресії;
· здійснювати економічний аналіз економетричної моделі.
Ключові поняття: множинна регресія; ендогенна змінна; екзогенна змінна; стохастична змінна в моделі; специфікація моделі; параметри регресії; оператор МНК; передумови застосування МНК; умови Гаусса – Маркова; система нормальних рівнянь у матричній формі; статистична значущість економетричної моделі; правило розкладання дисперсії; множинний коефіцієнт детермінації; скоригований коефіцієнт детермінації; F-критерій Фішера; стандартна похибка параметрів моделі; статистична значущість оцінок параметрів; t-критерій Стьюдента; інтервал довіри; інтервальний прогноз; точковий прогноз; похибка прогнозу; коефіцієнт еластичності; бета-коефіцієнт; дельта-коефіцієнт.
Теоретичні відомості
Як відомо, економічні величини формуються під впливом не одного, а цілої низки чинників, між якими можуть бути складні взаємозв'язки. Відтак вплив цих чинників комплексний, і його не можна розглядати як просту суму ізольованих впливів, інакше можна дійти неправильних висновків. Усе це приводить до необхідності застосовувати для дослідження складних економічних явищ багатофакторні моделі: 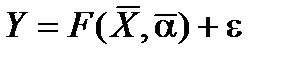 , де
, де 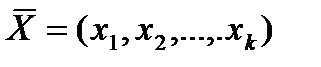 – факторні (пояснювальні) змінні;
– факторні (пояснювальні) змінні; 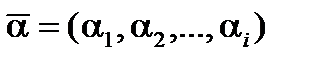 – істинні параметри моделі;
– істинні параметри моделі; 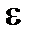 – стохастичне збурення (випадкова компонента, включення якої в рівняння зумовлене тими ж причинами, що й у разі парної регресії).
– стохастичне збурення (випадкова компонента, включення якої в рівняння зумовлене тими ж причинами, що й у разі парної регресії).
Вибір типу рівняння багатофакторної моделі ускладнений тим, що можна вибрати цілу низку рівнянь, які певною мірою описуватимуть зв'язок між результативним показником і факторними ознаками. Тому зазвичай досліджують декілька моделей. Поширеними в економічному аналізі функціями є: лінійна, степенева, показникова та деякі інші. Однією з найбільш застосовуваних моделей множинної регресії є лінійна модель. Вона досить поширена в макроекономічних розрахунках, у вивченні виробничих функцій, проблем попиту та ін.
Постановка задачі. Нехай є вибірка, що складається з n спостережень залежної змінної Y і пояснювальних змінних 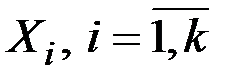 (табл. 8).
(табл. 8).
Таблиця 8
| № з/п
| Y
| X1
| X2
| ¼
| Xk
|
| 1
| Y1
| X11
| X12
| ¼
| X1k
|
| 2
| Y2
| X21
| X22
| ¼
| X2k
|
| ¼
| ¼
| ¼
| ¼
| ¼
| ¼
|
| n
| Yn
| Xn1
| Xn2
| ¼
| Xnk
|
За даними вибірки необхідно оцінити параметри лінійної моделі множинної регресії (ЛММР), яку в загальному вигляді записують таким чином: 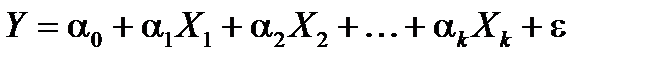 .
.
Для оцінки параметрів 
|
|
|





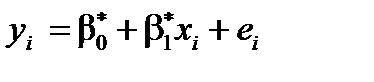 .
.
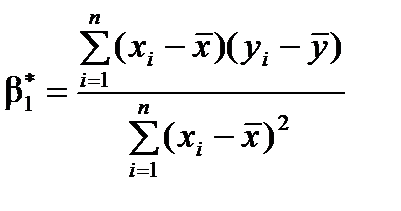 ,
, 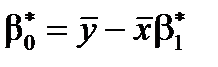 .
.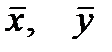 ,
, 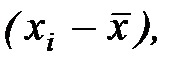
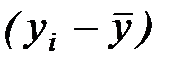 ,
, 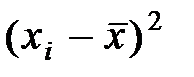 для кожного спостереження
для кожного спостереження 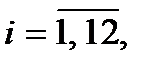 а також
а також 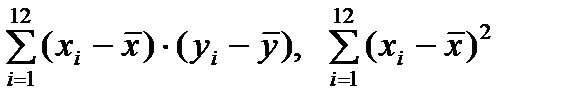 .
.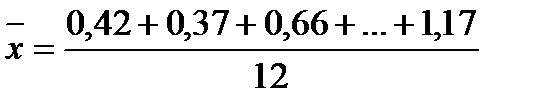 =0,7542,
=0,7542,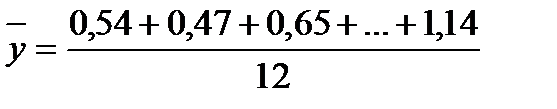 = 0,7858.
= 0,7858.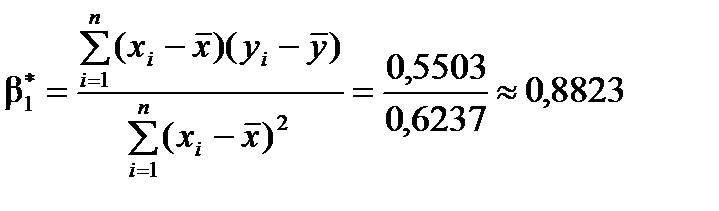 ,
, 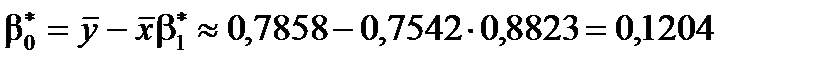 .
.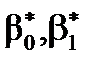 має вигляд
має вигляд 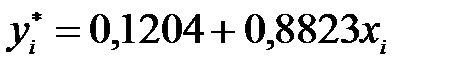 .
.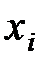
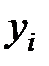
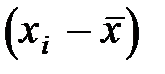
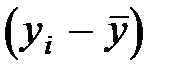
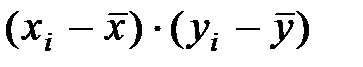
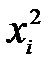
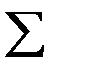
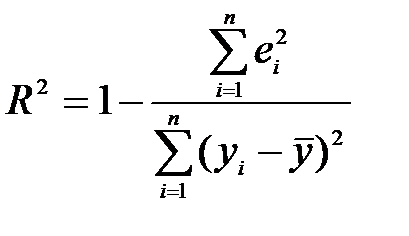 або
або 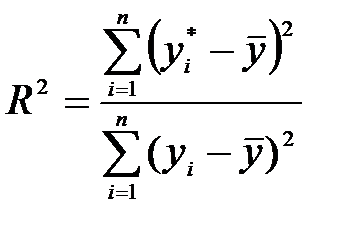 .
.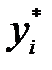 , відповідні значення
, відповідні значення 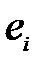 (розрахуємо їх як
(розрахуємо їх як 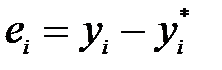 ), суми
), суми 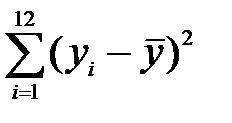 ,
, 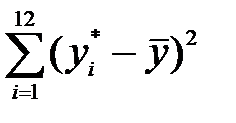 ,
, 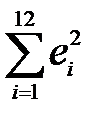 . Усі результати занесемо в табл. 7. На основі цих даних матимемо:
. Усі результати занесемо в табл. 7. На основі цих даних матимемо: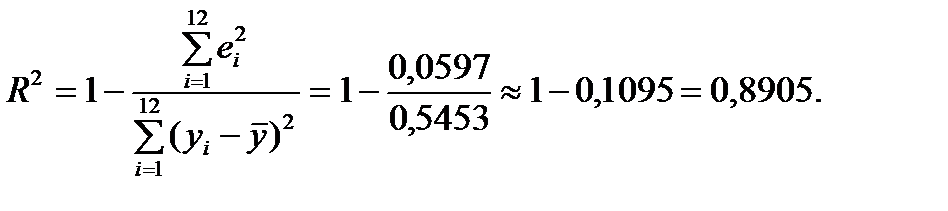
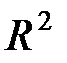 дозволяє визначити, наскільки добре емпіричне рівняння регресії узгоджується зі статистичними даними, тобто наскільки реальні значення відхиляються від побудованої лінії регресії. Для розглядуваного прикладу з рис. 5 можна побачити, що точки, відповідні реальним спостереженням, розташовані дуже близько від лінії регресії, отже, отриманий результат
дозволяє визначити, наскільки добре емпіричне рівняння регресії узгоджується зі статистичними даними, тобто наскільки реальні значення відхиляються від побудованої лінії регресії. Для розглядуваного прикладу з рис. 5 можна побачити, що точки, відповідні реальним спостереженням, розташовані дуже близько від лінії регресії, отже, отриманий результат 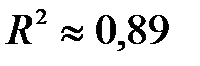 є цілком закономірний. Зробимо висновок: на 89% зміна обсягів реалізації продукції визначена зміною кредиторської заборгованості підприємства і лише на 11% такі зміни пов’язані з іншими (не врахованими в даній економетричній моделі) факторами.
є цілком закономірний. Зробимо висновок: на 89% зміна обсягів реалізації продукції визначена зміною кредиторської заборгованості підприємства і лише на 11% такі зміни пов’язані з іншими (не врахованими в даній економетричній моделі) факторами.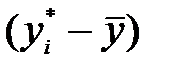
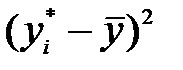
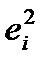
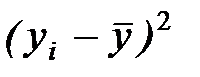
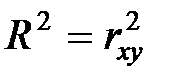 , обчислимо значення парного коефіцієнта кореляції
, обчислимо значення парного коефіцієнта кореляції 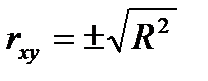 та перевіримо його статистичну значущість. Матимемо
та перевіримо його статистичну значущість. Матимемо 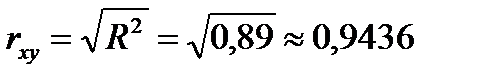 . Коефіцієнт кореляції є додатний, оскільки маємо пряму залежність між змінними х та у, що видно з рис.5.
. Коефіцієнт кореляції є додатний, оскільки маємо пряму залежність між змінними х та у, що видно з рис.5.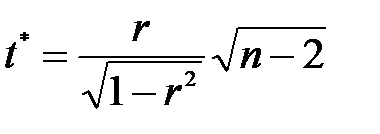 . Обчислене значення
. Обчислене значення 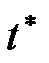 порівняємо з табличним значенням, вибраним за заданим рівнем значущості a і степенями вільності
порівняємо з табличним значенням, вибраним за заданим рівнем значущості a і степенями вільності 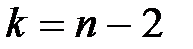 , на основі чого зробимо висновок стосовно прийняття гіпотези про значущість (незначущість) коефіцієнта кореляції:
, на основі чого зробимо висновок стосовно прийняття гіпотези про значущість (незначущість) коефіцієнта кореляції: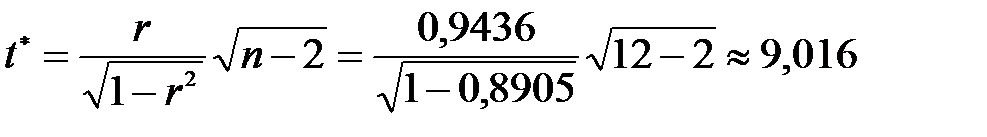 .
.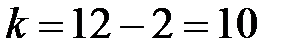 , то табличне значення
, то табличне значення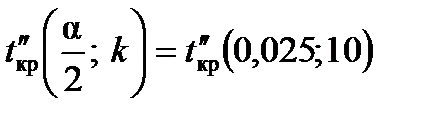 = 2,228;
= 2,228; 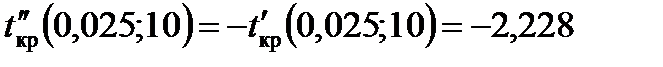 .
.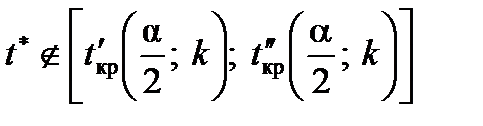 , приймемо гіпотезу про статистичну значущість розрахованого для розглядуваного прикладу коефіцієнта кореляції.
, приймемо гіпотезу про статистичну значущість розрахованого для розглядуваного прикладу коефіцієнта кореляції.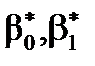 економетричної моделі
економетричної моделі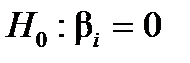 за альтернативної гіпотези
за альтернативної гіпотези 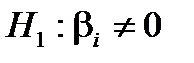 виберемо як статистичний критерій випадкову величину
виберемо як статистичний критерій випадкову величину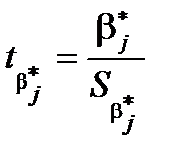 (
( 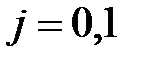 ).
).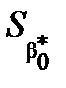 та
та 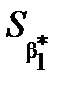 застосуємо формули
застосуємо формули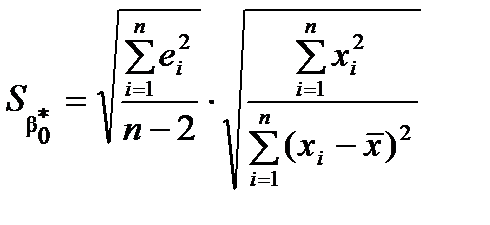 ,
, 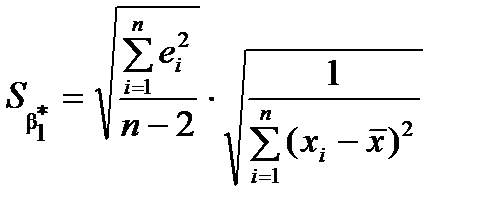 .
.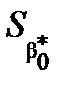 :
: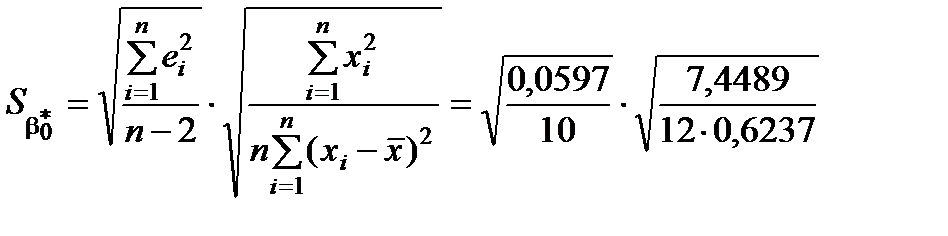

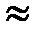 0,0773 × 0,99763
0,0773 × 0,99763 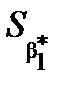 :
: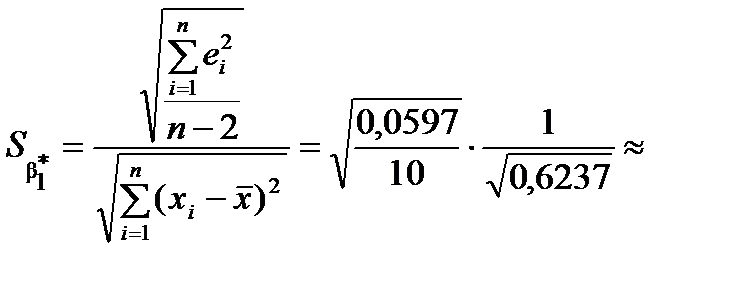 0,0773 × 1,2662
0,0773 × 1,2662 
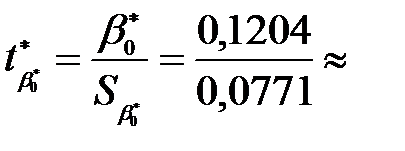 1,56 ,
1,56 , 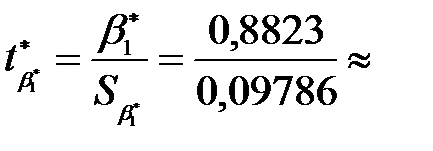 9,016.
9,016.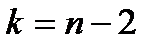 степенями вільності.
степенями вільності.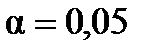 та кількості степенів вільності
та кількості степенів вільності 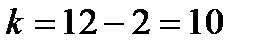 матимемо таке:
матимемо таке: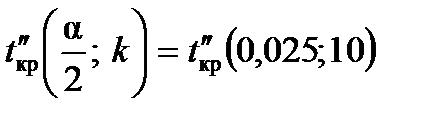 = 2,228,
= 2,228, 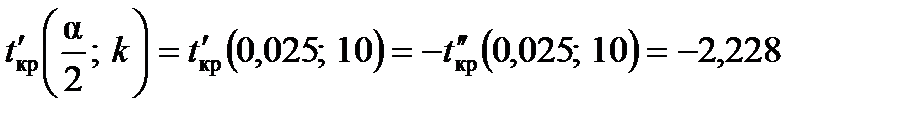 .
.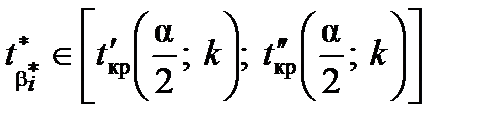 , слід прийняти гіпотезу про те, що
, слід прийняти гіпотезу про те, що 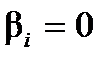 , і, навпаки,
, і, навпаки, 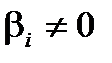 (
( 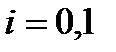 ), якщо
), якщо 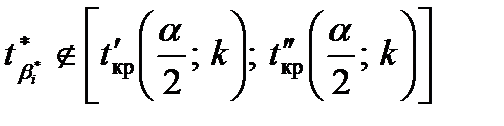 . Тобто область прийняття гіпотези, за якою
. Тобто область прийняття гіпотези, за якою 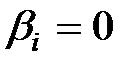 , визначена інтервалом
, визначена інтервалом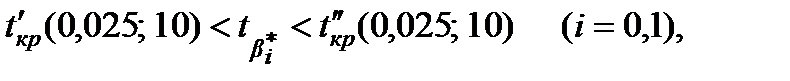
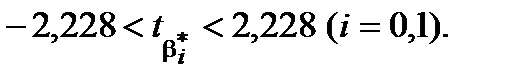
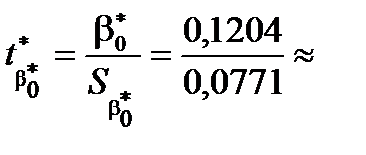 1,56
1,56 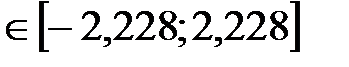 .
.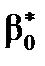 приймемо гіпотезу
приймемо гіпотезу 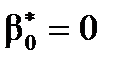 .
.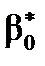 вказує на те, що всі інші фактори, не враховані в розглядуваній регресійній моделі, не роблять значного впливу на залежну змінну.
вказує на те, що всі інші фактори, не враховані в розглядуваній регресійній моделі, не роблять значного впливу на залежну змінну.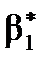 :
: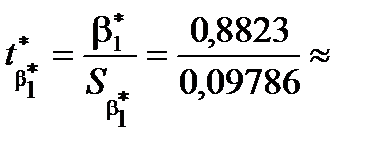 9,016
9,016 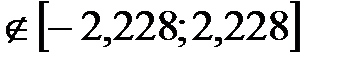 .
.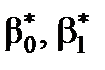 ) можна визначити модель як якісну, оскільки статистично значуща оцінка параметра
) можна визначити модель як якісну, оскільки статистично значуща оцінка параметра 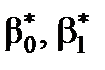 економетричної моделі
економетричної моделі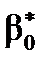 :
: 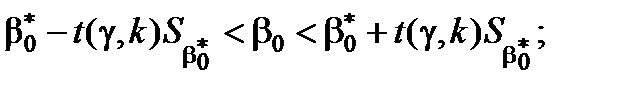
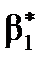 :
: 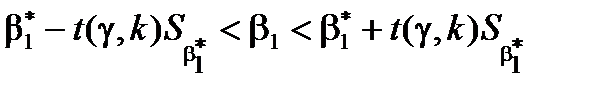 ,
,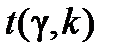 визначимо за допомогою таблиці за заданою надійністю g = 1-a і кількістю степенів вільності
визначимо за допомогою таблиці за заданою надійністю g = 1-a і кількістю степенів вільності 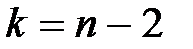 .
.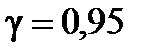 та, враховуючи, що кількість степенів вільності дорівнює
та, враховуючи, що кількість степенів вільності дорівнює 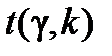 = 2,228. Отже, довірчі інтервали для оцінок параметрів визначені такими межами:
= 2,228. Отже, довірчі інтервали для оцінок параметрів визначені такими межами: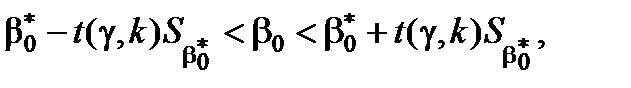
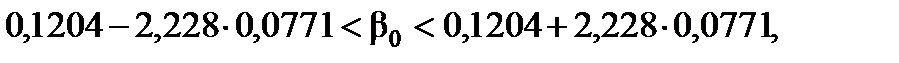
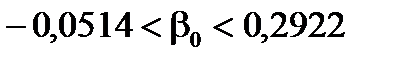 ,
,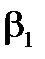 матимемо
матимемо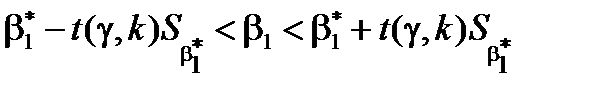 ,
,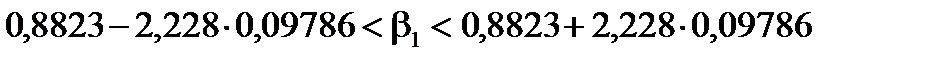 ,
,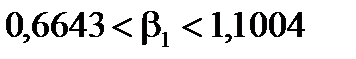 .
.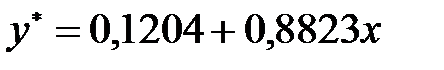 .
.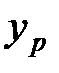 для значення
для значення 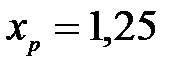 (точковий прогноз):
(точковий прогноз):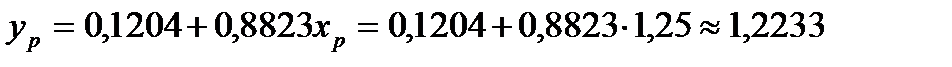

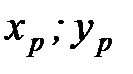 ) знаходиться на побудованій прямій, однак зрозуміло, що реальне значення
) знаходиться на побудованій прямій, однак зрозуміло, що реальне значення 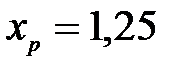 може відхилятися від лінії регресії, тому для розрахунку точних прогнозів визначають не одну точку, а прогнозний інтервал.
може відхилятися від лінії регресії, тому для розрахунку точних прогнозів визначають не одну точку, а прогнозний інтервал.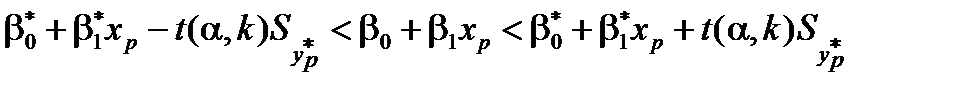 ,
,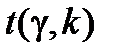 визначимо з допомогою таблиці за заданою надійністю
визначимо з допомогою таблиці за заданою надійністю 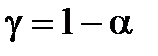 і кількістю степенів вільності
і кількістю степенів вільності 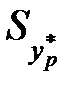 – похибка прогнозу, яку визначимо так:
– похибка прогнозу, яку визначимо так: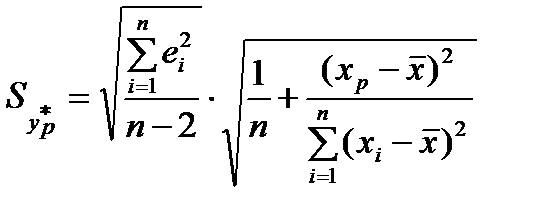 .
.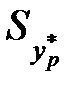 :
: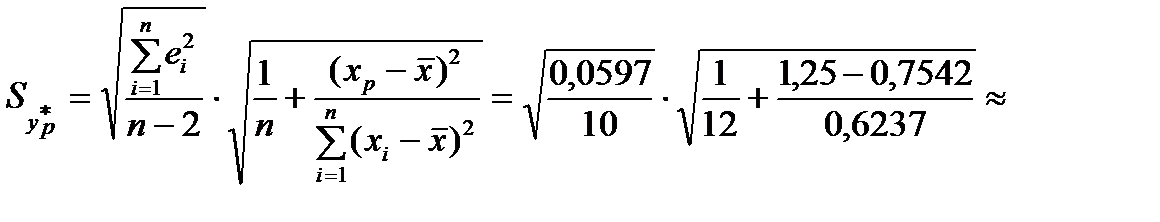
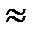 0,0773×0,937193
0,0773×0,937193 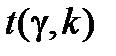 розрахуємо, як і в попередніх випадках, для
розрахуємо, як і в попередніх випадках, для 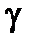 = 0,95 і кількості степенів вільності
= 0,95 і кількості степенів вільності 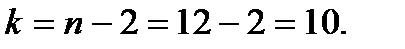 Матимемо
Матимемо 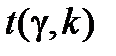 = 2,228. Таким чином,
= 2,228. Таким чином,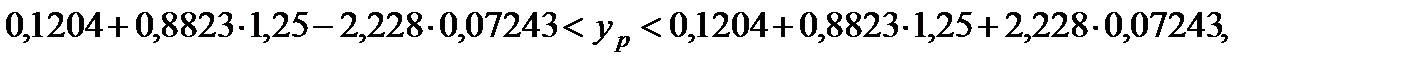
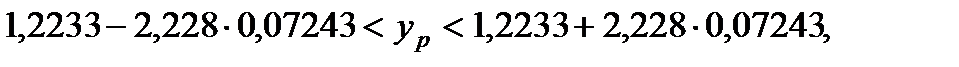
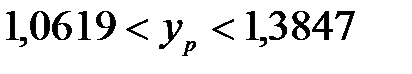 .
.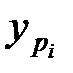 із заданою надійністю
із заданою надійністю 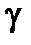 :
: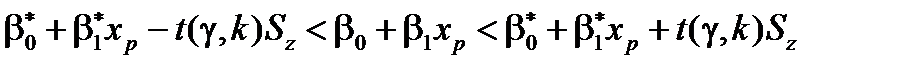 ,
,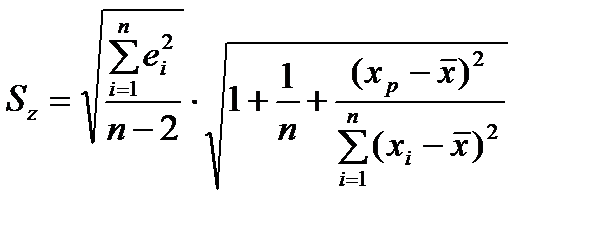 .
.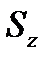 :
: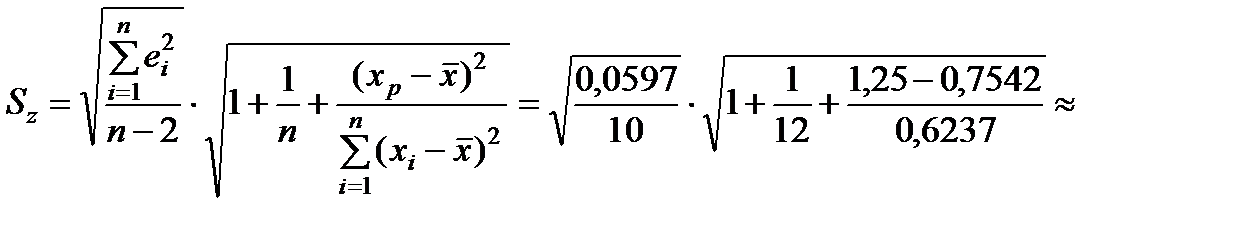
 1,484
1,484 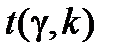 = 2,228 (для
= 2,228 (для 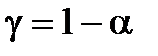 = 0,95 і кількості степенів вільності k = 10). Таким чином, межі прогнозного інтервалу складатимуть
= 0,95 і кількості степенів вільності k = 10). Таким чином, межі прогнозного інтервалу складатимуть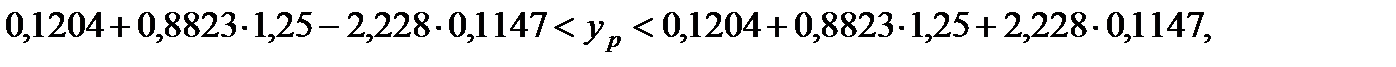
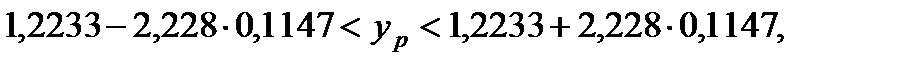
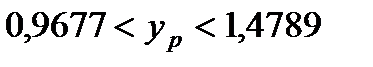 .
.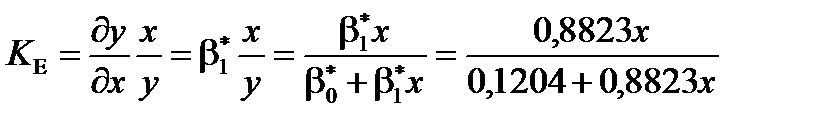 .
.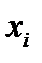 , коефіцієнт еластичності можна зобразити графічно (рис. 7).
, коефіцієнт еластичності можна зобразити графічно (рис. 7).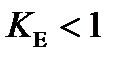 , тобто за зміни кредиторської заборгованості на 1% обсяг реалізації продукції змінюється менше ніж на 1%.
, тобто за зміни кредиторської заборгованості на 1% обсяг реалізації продукції змінюється менше ніж на 1%.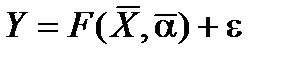 , де
, де 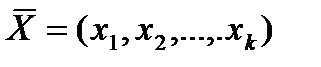 – факторні (пояснювальні) змінні;
– факторні (пояснювальні) змінні; 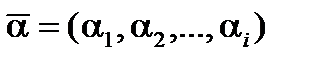 – істинні параметри моделі;
– істинні параметри моделі; 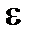 – стохастичне збурення (випадкова компонента, включення якої в рівняння зумовлене тими ж причинами, що й у разі парної регресії).
– стохастичне збурення (випадкова компонента, включення якої в рівняння зумовлене тими ж причинами, що й у разі парної регресії).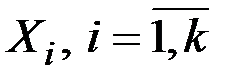 (табл. 8).
(табл. 8).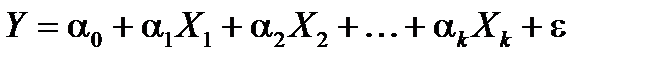 .
.


