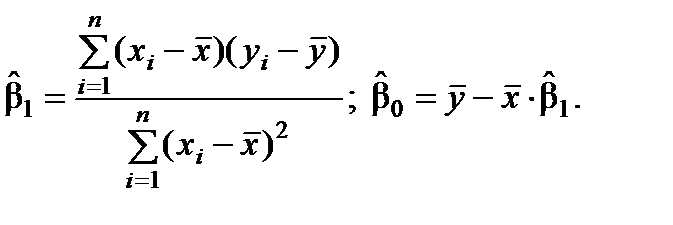Для оцінки параметрів регресій, лінійних за параметрами, застосовують МНК. Метод дозволяє отримати такі оцінки параметрів, за яких сума квадратів відхилень фактичних значень результативної ознаки у від теоретичних значень 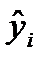 за тих самих значень фактора х мінімальна, тобто
за тих самих значень фактора х мінімальна, тобто
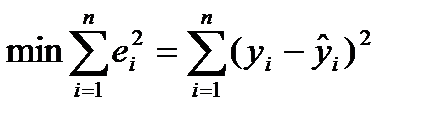 .
.
Геометричну ілюстрацію МНК показано на рис. 3.
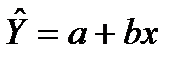
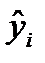

Рис. 3. Геометрична ілюстрація методу найменших квадратів
У випадку лінійної регресії 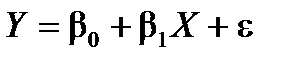 параметри знаходять із такої системи нормальних рівнянь:
параметри знаходять із такої системи нормальних рівнянь:
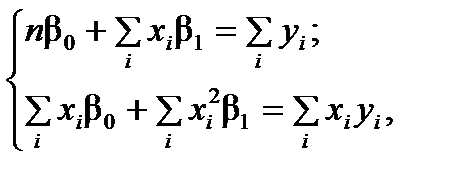
де n – кількість спостережень; 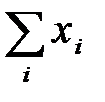 ,
, 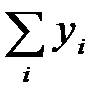 ,
, 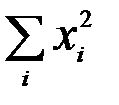 ,
, 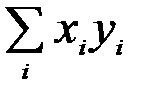 – величини, які можна розрахувати на основі вихідних спостережень за змінними Y і X.
– величини, які можна розрахувати на основі вихідних спостережень за змінними Y і X.
Розв’язавши подану систему, одержимо оцінки невідомих параметрів
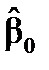 і
і 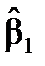 :
:
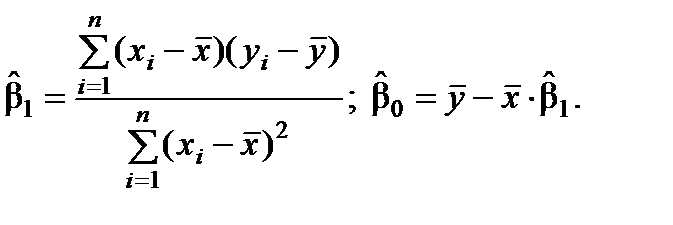
Зауваження .
1. МНК доцільно застосовувати тоді, коли виконуються такі передумови (гіпотези):
а) математичне сподівання залишків дорівнює нулю;
б) значення вектора залишків ε незалежні між собою й мають сталу дисперсію;
в) незалежна змінна моделі не зв’язана із залишками.
Ці гіпотези відомі як умови Гаусса – Маркова. У разі виконання цих умов МНК дозволяє створити найбільш відповідну емпіричним даним модель. Якщо деякі умови не виконуються, то необхідно застосовувати більш складні методи оцінювання.
2. Для нелінійних регресійних моделей, що є нелінійні відносно пояснювальної змінної, але лінійні за параметрами, МНК застосовують так само, як і у випадку лінійної регресії. До регресії, нелінійної за оцінюваними параметрами, залежно від вигляду функції можна застосовувати лінеаризуюче перетворення (буде описано далі).
Аналіз якості рівняння регресії як математичної моделі
Для практичного застосування економетричної моделі велике значення має її адекватність, тобто відповідність реальному процесу і тим статистичним даним, на основі яких побудовано модель.
Аналіз якості (верифікація моделі) включає перевірку:
- загальної якості рівняння регресії;
- статистичної значущості коефіцієнтів;
- точності моделі;
- властивостей, виконання яких було передбачено в ході оцінювання рівняння, наприклад умов Гаусса – Маркова (не входить до завдань цієї лабораторної роботи).





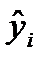 за тих самих значень фактора х мінімальна, тобто
за тих самих значень фактора х мінімальна, тобто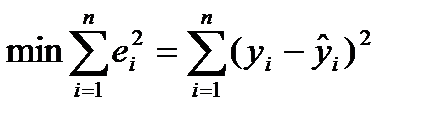 .
.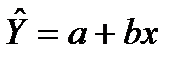
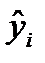

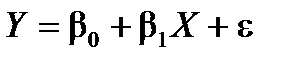 параметри знаходять із такої системи нормальних рівнянь:
параметри знаходять із такої системи нормальних рівнянь: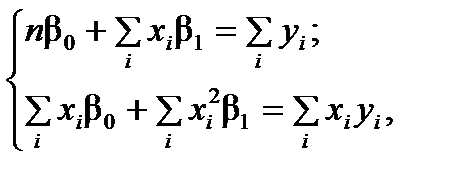
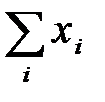 ,
, 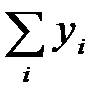 ,
, 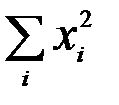 ,
, 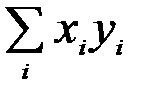 – величини, які можна розрахувати на основі вихідних спостережень за змінними Y і X.
– величини, які можна розрахувати на основі вихідних спостережень за змінними Y і X.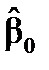 і
і 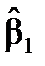 :
: