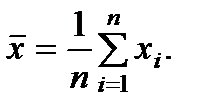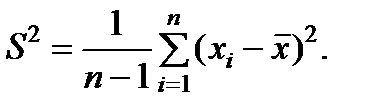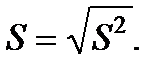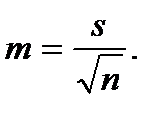Основні поняття математичної статистики

У результаті спостережень або експерименту отримують набори даних, називані вибірками. Для проведення їх аналізу дані піддають статистичній обробці. У ході обробки передусім завжди виконують обчислення елементарних статистичних характеристик вибірок (як мінімум середнього, середньоквадратичного відхилення, похибки середнього).

Серед вибіркових характеристик виділяють показники, стосовні центру розподілу (міри положення), показники розсіювання варіант (міри розсіювання) і міри форми розподілу. До показників, що характеризують центр розподілу, відносять різні види середніх (арифметичне, геометричне тощо), а також моду і медіану.

Найпростішим показником, що характеризує центр вибірки, є мода.
Мода – це елемент вибірки зі значенням, яке найбільш часто зустрічається (найбільш імовірна величина).

Середнє значення вибірки, або вибірковий аналог математичного сподівання, – це величина:

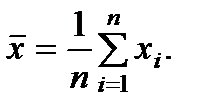
Інакше кажучи, середнє значення є центр вибірки, навколо якого групуються елементи вибірки. За збільшення кількості спостережень середнє наближається до математичного сподівання. Середнє значення також позначають буквою М.

Вибіркова медіана – це число, яке є серединою вибірки, тобто половина чисел має значення, більші медіани, а решта – значення, менші медіани. Для знаходження медіани зазвичай вибірку ранжують – розташовують елементи в порядку зростання. Якщо кількість членів рангового ряду непарна, медіаною є значення, розташоване посередині, тобто елемент з номером (n+1)/2. Якщо кількість членів ряду парна, то медіана дорівнює середньому членів ряду з номерами n/2 і n/2 + 1.

Основні показники розсіювання варіант – інтервал, дисперсія вибірки, стандартне відхилення і стандартна похибка.

Інтервал (амплітуда, варіаційний розмах) – це різниця між максимальним і мінімальним значеннями елементів вибірки. Інтервал є найпростішою і найменш надійною мірою варіації, розсіювання елементів у вибірці.

Більш точно відображають розсіювання показники, що враховують не тільки крайні, але всі значення елементів вибірки.

Дисперсією вибірки або вибірковим аналогом дисперсії називають величину

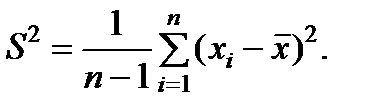
Дисперсія вибірки – це параметр, що характеризує ступінь розкиду елементів вибірки відносно середнього значення. Чим більша дисперсія, тим далі відхиляються значення елементів вибірки від середнього значення.

Вибірковим стандартним відхиленням (середнє квадратичне відхилення) називають величину

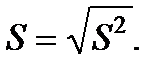
Цей параметр також характеризує ступінь розкиду елементів вибірки відносно середнього значення. Чим більше середнє квадратичне відхилення, тим далі відхиляються значення елементів вибірки від середнього значення. Параметр аналогічний дисперсії, його використовують у тих випадках, коли необхідно виразити показник розкиду випадкової величини в тих же одиницях, що й середнє значення цієї випадкової величини. Часто вибіркове стандартне відхилення позначають буквою s (сигма).

Стандартну похибку, або похибку середнього, знаходять із виразу

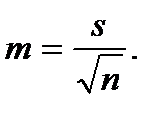
Стандартна похибка – це параметр, що характеризує ступінь можливого відхилення середнього значення, отриманого для досліджуваної вибірки, від істинного середнього значення, отриманого для всієї сукупності елементів. За допомогою стандартної похибки задають так званий довірчий інтервал.
Так, 95%-й довірчий інтервал, що дорівнює x ± 2m, позначає діапазон, у який з імовірністю р= 0,95 (за досить великої кількості спостережень n> 30) потрапляє середнє генеральної сукупності M.

Показниками форми розподілу є вибіркові ексцес і асиметрія.

Ексцес – це ступінь вираженості «хвостів» розподілу, тобто частоти появи віддалених від середнього значень. Коефіцієнт ексцесу характеризує крутість, тобто стрімкість підвищення, кривої розподілу порівняно з нормальною кривою.

Асиметрія – величина, що характеризує несиметричність розподілу елементів вибірки відносно середнього значення. Вона набуває значень
від -1 до 1. У разі симетричного розподілу асиметрія дорівнює нулю.

Часто значення асиметрії та ексцесу застосовують  для перевірки гіпотези про те, що дані (вибірка) належать до певного теоретичного розподілу, зокрема до нормального розподілу.

Для нормального розподілу мода дорівнює медіані та середньому, асиметрія дорівнює нулю, а ексцес – трьом.

Додаток 2