

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Интересное:
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Значущість усього рівняння в цілому оцінюють за допомогою F-критерію Фішера. Гіпотезу H0 про статистичну незначущість рівняння регресії (відсутність зв’язку між залежною і незалежною змінними) перевіряють порівнянням фактичного та критичного (табличного) значення F-критерію. Формула розрахунку фактичного F-критерію через коефіцієнт детермінації має вигляд
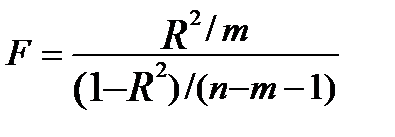 .
.
Фактичне значення F-критерію порівнюють із табличним значенням
F-розподілу Фішера за степенів вільності n – m і m – 1 (для парної регресії m=1) і вибраного рівня довіри.
Правило прийняття рішення
1. Якщо Fфакт > Fтабл, то гіпотезу H0 відхиляють та підтверджують значущість зв’язку ж залежною і незалежною змінними економетричної моделі, при цьому модель вважають надійною.
2. Якщо Fфакт < Fтабл, то гіпотезу H0 не відхиляють і визнають статистичну незначущість та ненадійність рівняння регресії.
Зауваження. Для моделі лінійної парної регресії статистичну значущість рівняння можна перевірити на основі коефіцієнта парної кореляції 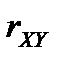 .
.
У цьому випадку 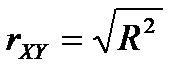 . Перевірку проводять за стандартною схемою статистичної перевірки гіпотез із застосуванням t-статистики Стьюдента.
. Перевірку проводять за стандартною схемою статистичної перевірки гіпотез із застосуванням t-статистики Стьюдента.
Розрахункове значення статистики складає 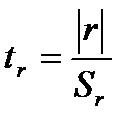 . У цій формулі значення
. У цій формулі значення 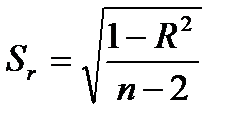 (стандартну похибку у визначенні величини
(стандартну похибку у визначенні величини 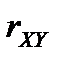 ) порівнюють із табличним
) порівнюють із табличним 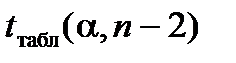 . Якщо
. Якщо 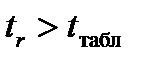 , то
, то 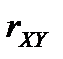 з вибраним рівнем довіри визнають статистично значущим, а модель – адекватною і надійною.
з вибраним рівнем довіри визнають статистично значущим, а модель – адекватною і надійною.
Для коефіцієнта кореляції можна побудувати довірчий інтервал:
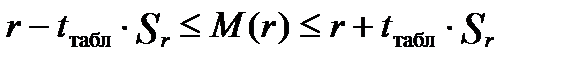 .
.
Чим ширший інтервал, тим більша невизначеність в оцінці зв'язку 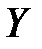 та
та 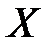 .
.
Перевірка точності моделі
Фактичні значення результативного показника відрізняються від теоретичних, розрахованих за рівнянням моделі, на величину 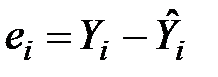 . Ця величина в кожному спостереженні є похибкою апроксимації. Відхилення
. Ця величина в кожному спостереженні є похибкою апроксимації. Відхилення 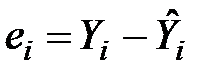 становлять абсолютну похибку, але вони непорівнянні між собою, оскільки залежать від одиниць виміру і масштабу величин
становлять абсолютну похибку, але вони непорівнянні між собою, оскільки залежать від одиниць виміру і масштабу величин 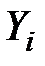 .
.
Так, якщо в одному спостереженні вийшла похибка 5, а в іншому – 10, це не означає, що в останньому випадку модель дає гірший результат. Тому для того щоб оцінки були порівнянними, розглядають відношення відхилень до фактичних значень (у процентах). Оскільки 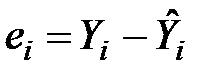 може бути як додатною, так і від’ємною величиною, то відхилення беруть за модулем.
може бути як додатною, так і від’ємною величиною, то відхилення беруть за модулем.
Визначення. Величину 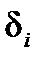 =
= 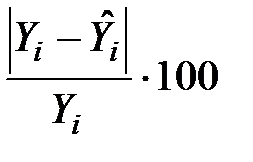 ,
, 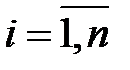 , називають відносною похибкою апроксимації в i-му спостереженні.
, називають відносною похибкою апроксимації в i-му спостереженні.
Щоб скласти загальне уявлення про точність моделі, визначають середню відносну похибку апроксимації:
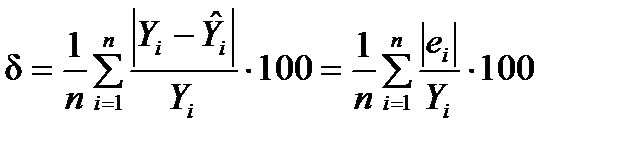 .
.
Похибка, менша 7–10%, свідчить про хороший підбір моделі до початкових даних (висока точність). У разі похибки, більшої 15%, слід вибрати інший тип рівняння моделі. В економетричному аналізі застосовують й інші алгоритми для розрахунку точності моделі.
|
|
|

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...
© cyberpedia.su 2017-2026 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!