Загальна якість рівняння регресії. Коефіцієнт детермінації

Як характеристику оцінки адекватності побудованої моделі або міри узгодженості розрахункових і фактичних значень Y доцільно застосовувати показник, що відбиває, якою мірою функція регресії визначена факторними (пояснювальними) змінними 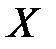, а якою – стохастичним збуренням e.

Розкид випадкової величини Y у вибірці можна виміряти за допомогою дисперсії: .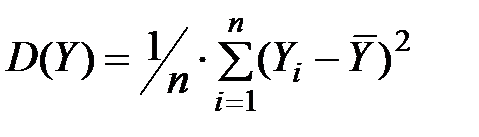

 

Розкладемо цю величину на складові. Очевидно, що

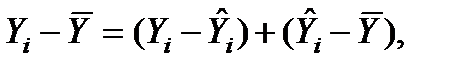
де .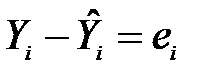

 

Графічно розкладання відхилень можна зобразити у вигляді рис. 8.

Рис. 8. Розкладання відхилень Y_i

від вибіркового середнього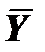

 

Оскільки 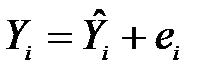, то 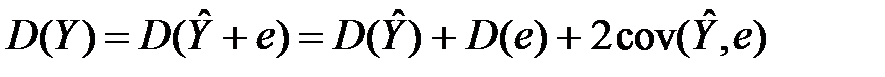. Легко перевірити, що 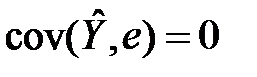. Тоді слушна така рівність, називана правилом розкладання дисперсії (варіацій):

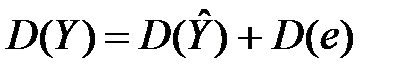.                                                (1)

Звідси можна записати співвідношення

.

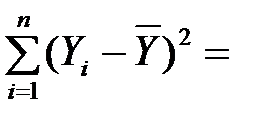
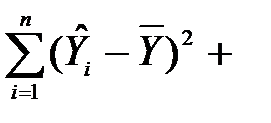
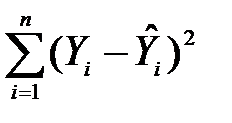Розкид фактичних значень 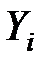 навколо середнього  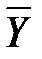вимірюють повною сумою квадратів:

TSS =  = .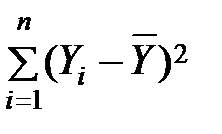

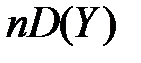Це загальне (повне) відхилення (total sum of squares, TSS).

Сума ESS = 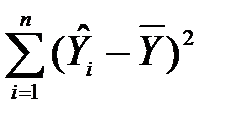= 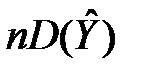визначає розкид розрахункових значень  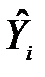навколо середнього  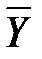і називається факторним відхиленням (explained sum of squares, ESS). Ця величина визначена включеними в рівняння факторними змінними 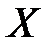, тому це відхилення називають також «поясненим».

Величина RSS= 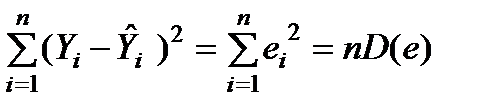 – залишкове відхилення (residual sum of squares, RSS). Це відхилення не можна пояснити кореляційною залежністю між Y та 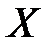, звідси його назва – «непояснене» або залишкове відхилення. Воно вимірює ту частину розсіяння, яка утворюється через вплив різних випадкових чинників. Тому чим ближче RSS до нуля, тим менше фактичні значення Y відхиляються від обчислених за рівнянням моделі значень 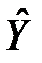. Таким чином, співвідношення (1) можна записати так: TSS=ESS+RSS.

 

Зауваження. Якість підбору функції можна встановити порівнянням двох оцінених дисперсій: дисперсії залишків і факторної дисперсії. Якщо RSS>ЕSS, то досліджуване рівняння визначає неадекватну модель, і її треба відкинути.

 

Якщо поділити співвідношення TSS=ESS+RSS на TSS, отримаємо

.

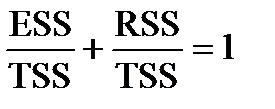Визначення. Величина 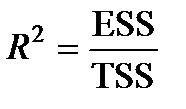 називається коефіцієнтом детермінації (мірою визначеності) та показує, яка частка загальної варіації аналізованої залежної змінної  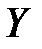визначена зміною факторних змінних.

Нагадаємо, що числове значення коефіцієнта детермінації знаходиться між нулем і одиницею. З отриманого співвідношення видно, що чим менше значення RSS, тим ближче 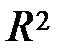 до одиниці і тим більш якісна (адекватна) модель.

Зауваження.

 1. Не слід абсолютизувати високе значення 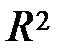, оскільки коефіцієнт детермінації може бути близьким до одиниці внаслідок того, що обидві досліджувані величини  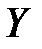та 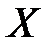 мають виражений часовий тренд, не пов'язаний з їх причинно-наслідковою залежністю. В економіці зазвичай такий тренд мають об'ємні показники (ВНП, ВВП, дохід та ін.). Тому в разі побудови й оцінки моделі за часовими рядами об'ємних показників величина  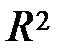може бути дуже близькою до одиниці, що не обов'язково свідчить про наявність значущого лінійного зв'язку між досліджуваними показниками.

2. Якщо рівняння регресії будують за перехресними даними, то коефіцієнт детермінації може бути не дуже високим навіть у випадку задовільної якості моделі через високі варіації між окремими елементами, зазвичай 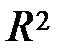 не перевищує 0,7. Те саме зазвичай має місце і для регресії за часовими рядами, якщо вони не мають вираженого тренда. У макроекономіці прикладами таких залежностей є: зв'язки відносних, питомих, темпових показників; залежність темпу інфляції від рівня безробіття; норми накопичення від величини процентної ставки та ін.

3. Нагадаємо, що точну межу прийнятності значення коефіцієнта варіації для всіх випадків відразу вказати неможливо. Можна керуватися оцінкою зв'язку, наведеною в шкалі Чеддока (див. табл. 4).

За умови 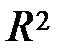=1 має місце функціональний зв'язок, а за 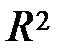=0 зв’язок відсутній. Якщо 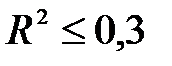, необхідно наново провести специфікацію моделі. В інших випадках потрібно враховувати, чи є змінні, що входять у модель, абсолютні або відносні, чи мають вони часовий тренд, який обсяг вибірки та ін.

4. Для моделі множинної регресії коефіцієнт детермінації є неспадною функцією кількості пояснювальних  змінних: додавання нової змінної ніколи не зменшує 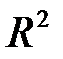. Дійсно, кожна наступна пояснювальна змінна може лише доповнити інформацію, що пояснює поведінку залежної змінної. Для нейтралізації цього недоліку коефіцієнта детермінації вводять скорегований коефіцієнт детермінації:

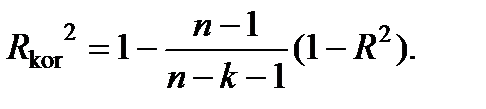
Очевидно, що 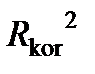 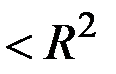для 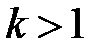. Із збільшенням кількості змінних скорегований коефіцієнт детермінації зростає повільніше, ніж звичайний, тобто він коригується в бік зменшення у випадку додавання пояснювальних  змінних. Доведено, що  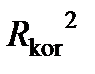збільшується за додавання нової пояснювальної змінної тільки тоді, коли t-статистика більша одиниці (тобто коефіцієнт перед цією змінною в рівнянні буде статистично значущим). Ця властивість може служити критерієм у випадку додавання до моделі нових пояснювальних  змінних.

F -критерій Фішера

Про існування залежності між 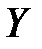 і факторними змінними ми судимо з величини 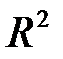. Постає питання, чи дійсно отримане в ході оцінки моделі значення  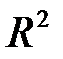відображає наявність істинної залежності або його отримали випадково.

Для перевірки статистичної значущості рівняння в цілому застосовують F-критерій Фішера, заснований на зіставленні факторної 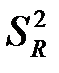 та залишкової  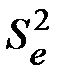оціночних дисперсій. Ця перевірка передбачає виконання нижчевказаних кроків.

Крок 1. Як нульову й альтернативну гіпотези розглядають такі:

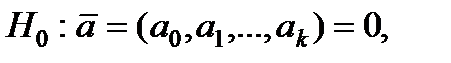
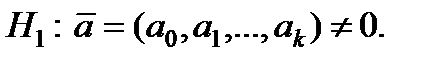
Крок 2. Обчислюють F-статистику: F= 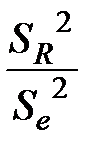, де 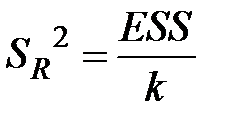;  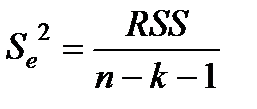(у чисельник формули завжди ставлять найбільшу величину).

Крок 3. У разі виконання гіпотези 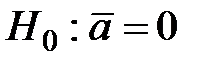 величини  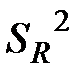і 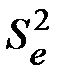 є незалежними і незміщеними оцінками однієї й тієї ж дисперсії 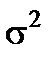, а їх відношення має F-розподіл Фішера з k та  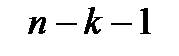степенями вільності. Англійський статистик Р. Е. Фішер визначив теоретичний розподіл відношення цих дисперсій, наведений у таблицях.

Крок 4. Використовують табличні значення 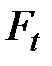 як критичні для оцінки розрахункових значень. Якщо F_розр>F_t, відкидають нульову гіпотезу і визнають рівняння статистично значущим. В іншому випадку приймають нульову гіпотезу про незначущість рівняння регресії.

Зауваження. F-статистику можна виразити через коефіцієнт детермінації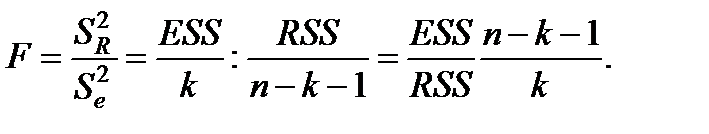

Поділимо останнє співвідношення на 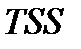 і отримаємо .

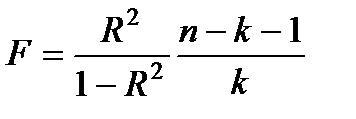Ця формула показує, що чим ближче коефіцієнт 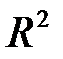 до одиниці, тим більше значення F, водночас малим значенням F (відсутність значущого зв’язку X та Y) відповідають малі значення R².