Оценка риска финансовых активов

Мера риска. Когда риск банкротства минимизируется в достаточной степени, на первый план выходит риск курсовой стоимости. Риск облигаций мерится доходностью. Акций – стандартным отклонением доходности (корень из дисперсии):

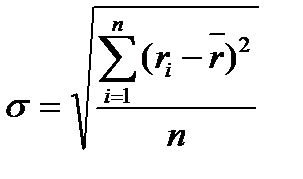[22]

Если числовая выборка меньше 30, то тогда для повышения точности расчетов «n» в знаменателе формулы заменяют на «n-1».

Если известно стандартное отклонение за год (σ), а надо узнать значение за меньший период:

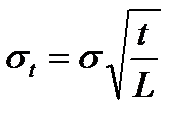[23]

t – период времени, для которого определяется стандартное отклонение;

L – количество торговых дней в году, в среднем 250 (если t также в днях).

 

При необходимости можно использовать коэффициент ковариации (p):

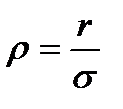[24]

Меняется ли риск в течении дня? Постановка вопроса: не проявляется ли в цене актива усталость брокеров, нарастающая, что звучит вроде как логично, к концу торгового дня? Если версия верна, то можно предположить, что в начале рабочего дня риск негативного изменения цены актива должен быть минимальным, а в конце – наоборот максимальным. Переложив все это на термины фондового рынка, приходим к следующему: в начале рабочего дня стандартное отклонение доходности финансового инструмента должно быть минимальным, а в конце – максимальным.

Предположение было проверено на четырех индексах – РТС, ММВБ, Доу Джонса и FTSE. Временной период ограничивался интервалом со 2 по 31 мая 2006 года и включал в себя только дни, когда была торговля. Для расчетов брались ежеминутные значения индексов, на основе которых считалось стандартное отклонение величины ежеминутного изменения индексов за каждый час в течение рабочего дня. Далее считалось среднеарифметическое стандартного отклонения за каждый час торгов в течении всего месяца (иначе говоря, складывались все значения для часа с 10=00 до 11=00 за период со 2 по 31 мая и находилось среднеарифметическое, потом для часа с 11=00 до 12=00 за тот же период и т.д.).

Рисунок 4.

Источник – сайт компании Финам (www.finam.ru), расчеты автора.

 

Анализ график позволил сделать следующие наблюдения.

• Во-первых, два индекса – ММВБ и FTSE – действительно показали небольшой рост стандартного отклонения индекса к концу торгов. Возможно, предположение о нарастании усталости инвесторов верно?
• Во-вторых, отмечено, что наибольшее значение стандартного отклонения приходится на первый час торгов. Можно подумать, что брокеры приходят на работу исключительно в возбужденном состоянии.
• В-третьих, уже со второго часа торгов значение стандартного отклонения сокращается в два-три раза и больше уже таких резких скачков не совершает.
• В четвертых, стандартное отклонение индексов ММВБ и FTSE сильно кореллирует друг с другом, чего не скажешь об индексах РТС и ММВБ, хотя, казалось бы, РТС и ММВБ – торговые площадки одной страны.
• В пятых, отечественный фондовый рынок (как среднее от ММВБ и РТС) рисковее зарубежного (в данном случае среднего от американского и английского) в 2,7 раза.

Еще раз про безрисковую процентную ставку. В традиционном понимании безрисковым признается такой финансовый инструмент, у которого нет колебаний курса, вызванных рыночными факторами. Это означает, что владелец облигации несет нулевой риск убытка при продаже бумаги в случае неожиданного уменьшения ее курса. Но на практике абсолютно безрисковых инструментов не бывает. Поэтому, исходя из принципа наименьшего зла (в нашем случае – наименьшего убытка), максимально безрисковым признается финансовый инструмент, имеющий наименьшее стандартное отклонение среди долговых ценных бумаг.

Value at risk, VaR. Параметр измерения риска в абсолютных цифрах. Призван ответить на вопрос: «Какой может оказаться потеря в стоимости актива, например в 95% случаев в течение следующего дня»? Существует две группы моделей VAR:

Параметрические – в них используется предположение, что доходность актива следует определенному виду вероятностного распределения, обычно нормального.

Непараметрические – считается, что нормальное распределение недооценивает вероятность получения более лучших и более худших результатов доходности актива, так как на практике у VaR более «толстые хвосты».

Базовая параметрическая модель:

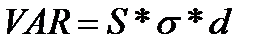[25]

S – стоимость актива (портфеля, проекта).

σ – стандартное отклонение доходности актива.

d – количество стандартных отклонений, соответствующих уровню доверительной вероятности (для 95% оно равно 1,645, для 90% – 1,282)

 

Пример. Доверительная вероятность 95%, стоимость портфеля 10 млн. ед., стандартное отклонение доходности портфеля в расчете на год – 25%, количество торговых дней в году – 250. Необходимо определить какую стоимость может потерять портфель с данной вероятностью в течении следующего дня.

Вначале определим стандартное отклонение в расчете на один день:

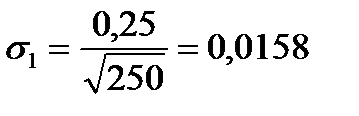
Теперь рассчитаем возможный размер потерь:

VaR = 10 млн. * 0,0158 * 1,645 = 261 тыс. ед.

Итак, в течении следующего дня с вероятностью 95% ожидается потеря до 261 тыс. ед. Вероятность потери большей суммы не превышает 5%.

Одна из разновидностей VaR, предлагаемых к применению для оценки риска проекта:

[26]

r – среднее значение доходности проекта (актива) за период.

 

Пример. Стоимость проекта 15 млн. ед., стандартное отклонение доходности инвестиций за год равно 22%. Среднегодовое значение доходности – 15%. Доверительная вероятность принята за 95%. Какой частью инвестиций рискует предприятие (в течении следующего года)?

VAR = 15 млн. (1,645 * 0,22 – 0,15) = 3,18 млн.

Итак, вероятность того, что (в течении следующего года) потери превысят 3,18 млн. ед. составляет всего 5%.

Обратите внимание, что в обоих формулах значение стандартного отклонения – не прошлое, а будущее: это прогнозное значение на оцениваемый период.

RAROC. С таким названием существует ряд коэффициентов, оценивающих риск. Рассмотрим один:

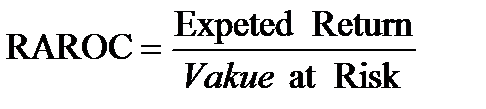
Expected return – тот доход, который может быть получен от инвестиций за вычетом ожидаемых потерь. Иначе говоря, рискуем суммой VaR, но рассчитываем получить ER. Тогда RAROC это измеритель доходности рисковых инвестиций.

Пример. Размер инвестиций составляет 1 млн. ед., ROI проекта – 35% (ожидаемый доход 350 тыс. ед.), однако существует риск потери 300 тыс. ед. дохода, что сводит ожидаемую доходность к сумме в 50 тыс., VAR проекта – 400 тыс. ед. Временной период для оценки проекта и для оценки VaR одинаков.

Соотнесем «гарантированно» ожидаемые доходы с «гарантированно» ожидаемыми потерями. RAROC равен 12,5% (50 тыс. / 400 тыс.), то есть на один рубль, которым компания гарантированно рискует, она получит лишь 12,5 копеек гарантированного дохода. Это очень низкое значение, поскольку возможные потери составляют несравнимо большую величину, нежели приобретения.

 

ОЦЕНКА СТОИМОСТИ ОПЦИОНОВ

Опционные зарплатные программы. Обычно одно только сообщение о принятии опционной программы повышает стоимость акций. Также и обеспечение программы приводит к росту стоимости. Например, с 08.2004 г. по 09.2004 г. РАО ЕЭС приобрело на рынке 1% от УК для обеспечения опционной зарплатной программы, что составляло примерно 10% от количества обращающихся на рынке акций, что изменило текущую цену акции с 8 рублей до 9,5 рублей.

Фантомный опцион – вместо акций выплата деньгами. Нет необходимости резервировать акции под будущие выплаты.

Проблемы – Компания не может напрямую владеть собственными акциями более 1 года (привлечение в программу иностранных юридических лиц). Кроме того, неденежная форма выплаты зарплаты не может превышать 20%.

Возможные махинации – Фиксирование цены опциона накануне выхода позитивных новостей.

Биноминальная модель. Древо решений. Основные необходимые параметры: средняя доходность и стандартное отклонение доходности акций компании.

Основные условия. Время поделено на периоды. Курс акции может принимать только два значения или подняться или снизиться. Сам курс цены не имеет принципиального значения, поскольку покупатель и продавец всегда имеют противоположные представления о предстоящем изменении стоимости акции.

Альтернативный портфель: можно составить такой портфель, состоящий из акций компании и депозита в банке «у», денежные потоки которого через один период будут такими же как и у опциона. Следовательно этот портфель будет стоить столько же сколько и опцион.

Обратите внимание и примите к сведению:

• В рамках биноминальной модели досрочное исполнение опциона колл не приносит ожидаемой доходности.
• Значения доходности и стандартного отклонения рассчитаны исходя из прошлых значений и просто распространяются на будущие значения курса актива. Но этот порядок не бесспорен.
• Отрицательная величина «у» оказывает, что на депозит размещены средства, взятые в долг.
• Биноминальная модель не принимает в расчет вероятность повышения или понижения курса акций. Это не существенно, поскольку у покупателя и продавца сложились противоположные ожидания о движении курса акций. А иначе не состоялась бы сама сделка.

Формула Блэка-Шоулза.

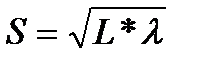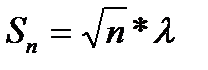или [27]

S – смещение, то есть расстояние по прямой от точки начала движения частицы до точки окончания ее маршрута.

L – длина всего пути, пройденного частицей.

n – количество перемещений, или сколько раз частица меняла направление движения.

λ – средняя длина одного перемещения.

 

Стоимость европейского опциона колл, по которому не выплачиваются дивиденды:

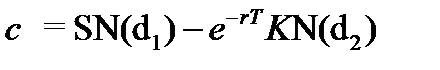[28]

Если говорить совсем упрощенно: с = выгоды – приведенные издержки

S – цена акции в момент выпуска опциона, K – цена исполнения опциона, r – безрисковая процентная ставка, T – срок опциона, N(d) – функция логнормального распределения.

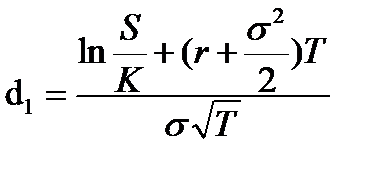, [29]

σ – стандартное отклонение доходности акций.

 

Обратите внимание на интересную деталь: доходность акции в формуле впрямую не представлена.

Цена опциона увеличивается в результате роста таких параметров, как цена акции, неопределенность, срок исполнения опциона и процентная ставка по безрисковым активам. Уменьшается она вследствие возрастания цены исполнения и дивидендов.

Следовательно:

• бессрочные опционы являются наиболее более ценными.
• в условиях кризиса стоимость опциона возрастает.

Для случая с акциями, по которым выплачивается дивиденд, в формулы предлагается внесение дополнения (δ - дивиденды):

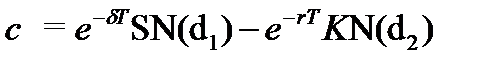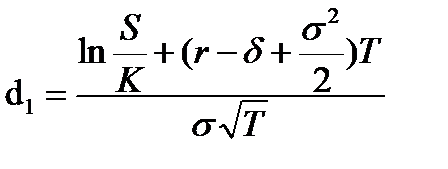, [30]

Реальные опционы. Приложение финансовых технологий для реального сектора экономики. «Реальный опцион» – опцион, «скрытый» в балансе, а не торгуемый на бирже.

Для реального сектора экономики эквиваленты факторов формулы определяются следующим образом.

Цена акции (S) — текущая стоимость денежных потоков, ожидаемых от реализации той инвестиционной возможности, на право использования которой приобретен опцион.

Цена исполнения (К) — текущая стоимость всех постоянных издержек, которые предполагается понести в период реализации инвестиционной возможности.

Неопределенность (σ) — невозможность точного определения размеров будущих денежных потоков, связанных с данным активом. Если сформулировать более строго, это среднее квадратическое отклонение темпов роста будущих притоков денежных средств.

Срок действия опциона (T) — период, в течение которого инвестиционная возможность остается открытой. Он зависит от технологии (продолжительности жизненного цикла товара), конкурентных преимуществ (интенсивности конкуренции) и условий контрактов (патентных, лизинговых, лицензионных).

Дивиденды (δ) — стоимость, теряемая в течение срока действия опциона. Это могут быть расходы, понесенные в целях сохранения опциона (путем оттеснения конкурентов или создания необходимых условий для поддержания инвестиционной возможности), а также потеря части денежных потоков в пользу конкурентов, которые раньше приступили к реализации инвестиционной возможности (в формуле используется не абсолютная величина дивидендов, а ставка дивиденда в виде десятичной дроби).

Процентная ставка по безрисковым активам (r) — доходность безрисковых ценных бумаг, срок погашения которых тот же, что и срок действия опциона.

Эквиваленты параметров в случае строительства:

• текущая стоимость актива – стоимость строительно-монтажных работ;
• цена исполнения – стоимость построенного объекта.

Обратите внимание:

• Бухгалтерский учет – учет прошлой разницы между выручкой и расходами.
• Дисконтирование – учет будущих денежных потоков (учет риска).
• Применение опционного ценообразования – еще и учет будущей неопределенности.

Изменчивость опциона. Дельта опциона отвечает на вопрос: на сколько денежных единиц изменится цена опциона, если курс базового актива повысится или понизится на 1 денежную единицу и при этом остальные факторы, влияющие на цену опциона, останутся неизменными.

Пример. Курс акций изменился на 12,5 ед. с 269 до 281,5. Цена опциона колл на эту акцию изменилась на 5,3 ед. с 37,4 до 40. Тогда дельта опциона составляет:

5,3/12,5 = 0,42

Эластичность опциона, µ (модель Пауля Самуэльсона и Генри МакКина для оценки стоимости земли как опциона, 1965 год). Отражает процент изменения стоимости незастроенной земли при 1%-ном изменении рыночной стоимости введенной в эксплуатацию недвижимости.

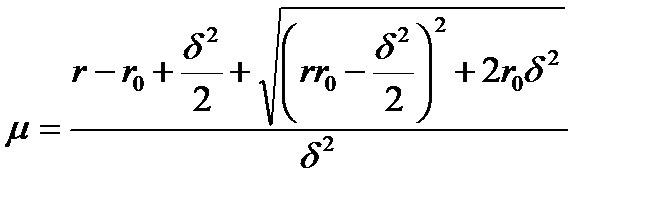[31]

r – ставка доходности на вложенный капитал

σ – стандартное отклонение стоимости недвижимости.

 

БИБЛИОГРАФИЯ

1. Гитман Л.Дж., Джонк М.Д. Основы инвестирования. М: Дело, 1997.

2. Бирман Г., Шмидт С. Капиталовложения. Экономический анализ инвестиционных проектов. М.: ЮНИТИ-ДАНА, 2003.

3. Стивен Росс, Рэндольф Вестерфилд, Брэдфорд Джордан. Основы корпоративных финансов. М.: Лаборатория Базовых знаний, 2000.

4. Брейли Р., Майерс С. Принципы корпоративных финансов. М.: Олимпик Бизнес, 1997.

5. Секреты инвестиционного дела. Под ред. Дж. Пикфорда. М.: Олимп-Бизнес, 2006.

6. Марк П. Крицман. Головоломки финансов. Шесть блистательных решений приумножения капитала. М.: ГроссМедиа, 2005.

7. Шарп У.Ф., Александер Г.Дж., Бейли Д.В. Инвестиции. М.: ИНФРА--М, 1998.

8. Бронштейн Е.М. Пособие по финансовой математике Уфа: Изд.УГАТУ, 1999.

9. Балабанов И.Т. Основы финансового менеджмента. Как управлять капиталом? Изд. 2-е. М.: Финансы и статистика, 1997.

10.Галиц Л. Финансовая инженерия: инструменты и способы управления финансовым риском. М.: ТВП, 1998.

11.Мориц Адельмейер. Опционы колл и пут. М.: Финансы и статистика, 2004.

12.Буренин А.Н. Рынок ценных бумаг и производных финансовых инструментов. М.: Научно-техническое общество им. С.И. Вавилова, 2002.

13.Белолипецкий В.Г. Финансовый менеджмент. М.: КНОРУС, 2006.

14.Reinhart C. and K. Rogoff. The modern history of exchange rate arrangements: a reinterpretation, Working paper, International Monetary Fund, 2003.

15.Carter D., Pantzalis Ch., and B. Simkins. Asymmetric exposure to foreign exchange risk: financial and real option hedges implemented by U.S. multinational corporations, Working paper, Oklahoma State University and University of South Florida, 2003.

16.Allayannis G. and J. Weston. The use of foreign curren cy derivatives and firm market value. The Review of Financial Studies, 2001,Vol. 14(1), pp. 243276.

17.Sohnke B., Brown G., and F. Fehle. International evidence on financial derivatives usage, Unpublished working paper, Lancaster University and University of North Carolina at Chapel Hill, 2003.

18.Bodnar, G. Jaguar plc. 1984. Case discussion, mimeo, Wharton School, University of Pennsylvania, 2004.

19.Williamson R. Exchange rate exposure and competetion: evidence from the automotive industry, Journal of Financial Economics, 2001, Vol. 59(3), pp. 441475.

20.Pritamani M., Shome D., and V. Singal. Foreign exchange exposure of exporting and importing firms, Working paper, Frank Russell Company and Virginia Tech., 2003.

21.Allayannis G., Brown G., and L. Klapper. Capital structure and financial risk: evidence from foreign debt use in East Asia, Journal of Finance, 2003, pp. 26672710.

22.Susmel R. Currency risk management at the firm level, mimeo, University of Houston, 2000.

23.Uppal R. Measuring and managing exposure to ex change rates, mimeo, 1999.

 

Ресурсы Интернета

1. http://www.finrisk.ru Сайт “Управление финансовыми рисками”.

2. http://www.hf.ru/rm/rm.htm Материалы по управлению рисками на сайте "Специализированного межрегионального Хеджевого Фонда".

3. http://www.moneysphere.f2s.com Финансово-образовательный портал “Moneysphere”.

4. http://www.aurora.ru/index.php?ind=rp_hayam Риск: Основные тезисы и принципы. Цели и стратегия. Организационная структура и функции.

5. http://www.finrisk.ru Управление финансовыми рисками. Теория и практика.

6. http://www.risks.ru/project/modulufr.htm Институт управления рисками.

7. http://www.riskcontrol.ru Центр Статистических Исследований.

8. rrm.rea.ru сайт "РЭА Риск-менеджмент".

9. www.FinPort.ru Риск-портал "РЭА Риск-менеджмент".

10.www.riskman.ru сайт Института Управления Рисками при Государственном Университете Управления.

11.www.mbkcentre.com Сайт, посвященный анализу коммерческих банков.

12.www.risk-management.ru Сайт компании РМ-Технологии.

13.http://www.hf.ru/an/articles/hedge Статьи по хеджированию.

14.www.bashedu.ru/konkurs/bakirov/aug/uprav.htm Сборник статей по управлению рыночными рисками.

15.www.bizcom.ru журнал "Бизнес и компьютер". В архиве ряд публикаций посвящено управлению рисками.

16.www.bdm.ru журнал "Банковское дело в Москве". В архиве ряд публикаций посвящено управлению рисками.

17.www.bankir.ru форумы по банковской деятельности. В частности в разделе "Отчетность, риски" активно обсуждаются вопросы управления рисками.

18.trading.narod.ru/mmanage_index.htm статьи по управлению рисками и управлению капиталом.

19.www.iia-ru.divo.ru/info3.html статьи на сайте Московского клуба внутренних аудиторов.

20.www.forinfo.ru/MainPage/library.asp?l_s=2&p_id=4 статьи, касающиеся риск-менеджмента на сайте компании WestWind Trading.

21.www.dol.ru/users/partad/insurance/seminar.html Материалы семинаров ПАРТАД по управлению рисками (риски депозитарной деятельности, риски учетных систем).

22.www.geocities.com/WallStreet/Market/4444/ Информация по валютным рискам.

23.cslab.mipt.ru Лаборатория Computer Science. МФТИ. Материалы посвященные управлению финансами и в частности управлению рисками.

24.www.caravan.ru/~ankil/publish/archive_ur/ur_start.html журнал "Управление финансовыми рисками" - анонсы статей.

25.www.nsu.ru/ef/tsy/ecmr/garch/index.htm Материалы по GARCH-моделям.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Если цена облигации растет, то ее доходность … растет или падает?
2. Если доходность облигации растет, то ее риск … растет или падает?
3. От чего зависит доходность акции?
4. Что такое дюрация?
5. Как определить стоимость акции если дивиденды по ней не выплачиваются?
6. Если доходность равна размеру купона (9%), а номинал равен 1000 ед., чему равна текущая стоимость облигации (PV)?
7. Согласно формуле оценки стоимости акции, стоимость акции сразу после выплаты дивиденда должна соответственно сократиться. Почему обычно этого не происходит?
8. Считается, что акционеры крайне негативно относятся к идее выплаты дивидендов, первый платеж по которым будут выплачен только через сто лет, независимо от размеров дивиденда. Почему?
9. Риск в течении дня меняется, это факт. А меняется ли он в течении недели? Как это может выглядеть?
10. В какой день недели лучше всего объявлять плохие финансовые и корпоративные новости?
11. Насколько реально считать VaR на год вперед? Может при этом изменить значение доверительной вероятности?
12. Как определяется стоимость опциона?
13. Чем отличается биноминальная модель оценки стоимости опционов от формулы Блэка-Шоулза?

Вопросы по безрисковой процентной ставке:

• Понятно, что речь идет о государственных облигациях, но каких именно: внутренних или еврооблигациях?
• Речь идет о доходности в прошлом (ведь мы считаем дисперсию прошедшего периода) или о доходности к погашению? Или о доходности за период владения?
• А если у инструмента с наименьшим стандартным отклонением, отрицательная доходность, как тогда быть?
• А если на рынке имеется несколько инструментов с одинаково наименьшим стандартным отклонением, как тогда выбирать?
• А если сделать портфель, состоящий из нескольких бумаг, и имеющий в итоге наименьшее стандартное отклонение. Не будет ли доходность такого портфеля настоящей безрисковой?