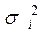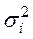Гетероскедастичність призводить до неефективності оцінок, незважаючи на їх незміщеність. Це може призвести до необґрунтованих висновків щодо якості моделі. Тому при встановленні гетероскедастичності виникає необхідність перетворення моделі з метою усунення даного недоліку. Вид перетворення залежить від того, відомі чи ні дисперсії відхилень. Метод зважених найменших квадратів (ВНК)
Даний метод застосовується при відомих для кожного спостереження значеннях . У цьому випадку можна усунути гетероскедастичність, розділивши кожне значення, що спостерігається на відповідне йому значення дисперсії. У цьому суть методу зважених найменших квадратів.
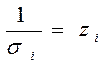 Для простоти викладу опишемо ВНК на прикладі парної регресії:
Для простоти викладу опишемо ВНК на прикладі парної регресії: 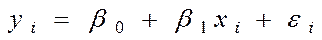 Розділимо обидві частини (7.5) на
Розділимо обидві частини (7.5) на 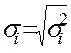 , одержимо:
, одержимо: 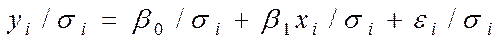 (6) Поклавши рівним
(6) Поклавши рівним 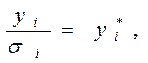
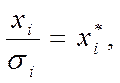
 одержимо рівняння регресії без вільного члена, але з додаткової пояснюючою змінної і з “перетвореним” відхиленням :
одержимо рівняння регресії без вільного члена, але з додаткової пояснюючою змінної і з “перетвореним” відхиленням :
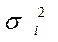
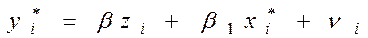 Для застосування ВНК необхідно знати фактичні значення дисперсій відхилень. На практиці такі значення відомі вкрай рідко. Отже, щоб застосувати ВНК, необхідно зробити припущення про значення .
Для застосування ВНК необхідно знати фактичні значення дисперсій відхилень. На практиці такі значення відомі вкрай рідко. Отже, щоб застосувати ВНК, необхідно зробити припущення про значення .
Наприклад, можна припустити, що дисперсії 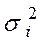 відхилень
відхилень 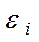 пропорційні значенням
пропорційні значенням 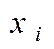 (рис. 9) чи значенням
(рис. 9) чи значенням 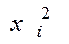 (рис. 10).
(рис. 10). 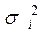
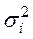

Методи усунення автокореляції. Авторегресійне перетворення.
Серед основних методів усунення автокореляції можна виділити:
1. Правильну специфікацію моделі (залучення значущих факторів або зміна форми залежності). Основною причиною наявності випадкової величини в узагальненій кореляційно-регресійній моделі є неможливість урахувати всі значущі фактори і взаємозв'язки,що зумовлюють певне значення результуючої змінної. Потрібно спробувати ідентифікувати факторну ознаку, яку не враховано в КРМ і врахувати її. Також можна спробувати змінити форму залежності( наприклад, лінійну на нелінійну).
2. Використання AR(1)-моделі (авторегресійної моделі Маркова 1-го порядку). Якщо віс доступні процедури зміни специфікації моделі вичерпані,а автокореляція наявна,то можна припустити, що вона обумовлена внутрішніми властивостями певних значень випадкових відхилень . У цьому разі можна скористатися авто регресійним перетворенням. У лінійній кореляційно-регресійній моделі або в моделях, що зводяться до лінійної, найдоцільнішим і простим перетворенням є авто регресійна модель Маркова першого порядку AR(1).





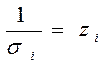 Для простоти викладу опишемо ВНК на прикладі парної регресії:
Для простоти викладу опишемо ВНК на прикладі парної регресії: 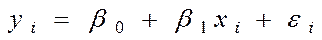 Розділимо обидві частини (7.5) на
Розділимо обидві частини (7.5) на 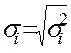 , одержимо:
, одержимо: 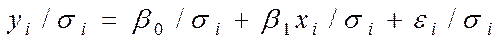 (6) Поклавши рівним
(6) Поклавши рівним 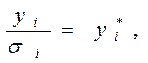

 одержимо рівняння регресії без вільного члена, але з додаткової пояснюючою змінної і з “перетвореним” відхиленням :
одержимо рівняння регресії без вільного члена, але з додаткової пояснюючою змінної і з “перетвореним” відхиленням :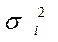
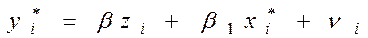 Для застосування ВНК необхідно знати фактичні значення дисперсій відхилень. На практиці такі значення відомі вкрай рідко. Отже, щоб застосувати ВНК, необхідно зробити припущення про значення .
Для застосування ВНК необхідно знати фактичні значення дисперсій відхилень. На практиці такі значення відомі вкрай рідко. Отже, щоб застосувати ВНК, необхідно зробити припущення про значення .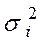 відхилень
відхилень 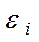 пропорційні значенням
пропорційні значенням 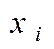 (рис. 9) чи значенням
(рис. 9) чи значенням 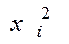 (рис. 10).
(рис. 10).