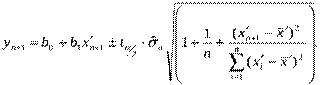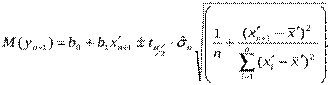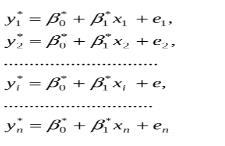
Нелінійні моделі та їх лінеаризація. Приклади використання в економіці.
Найбільш популярною моделлю в економіці є лінійна регресія. Проте не всі економічні процеси можна нею моделювати. Тому на практиці використовуються складніші моделі з нелінійною залежністю між показником у та фактором х. За методикою оцінок параметрів парні нелінійні регресії розглядаються двох видів: 1) нелінійні за факторами, але лінійні за невідомими параметрами, які підлягають оцінці; 2) нелінійні за факторами і параметрами. Регресії, нелінійні за факторами, але лінійні за оцінюваними параметрами, називаються квазілінійними.
Парну квазілінійну регресію можна записати в загальному вигляді: 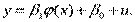 Заміною величин
Заміною величин 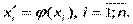 нелінійна парна регресія приводиться до лінійної парної регресії:
нелінійна парна регресія приводиться до лінійної парної регресії:  Формули для оцінок параметрів набувають вигляду
Формули для оцінок параметрів набувають вигляду
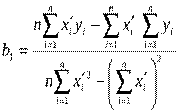 ,
, 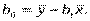
Коефіцієнт еластичності для парної квазілінійної регресії оцінюється за формулою 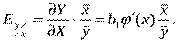 Для оцінки коефіцієнта еластичності нелінійної регресії в загальному використовується формула:
Для оцінки коефіцієнта еластичності нелінійної регресії в загальному використовується формула: 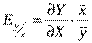 , де
, де 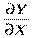 - частинна похідна функції у за змінною х.
- частинна похідна функції у за змінною х.
В регресіях нелінійних за факторами та параметрами логарифмують праву та ліву частину рівняння і проводять заміну змінних. Таким чином нелінійна регресія зводиться до лінійного виду. Параметри лінійної моделі оцінюють за відомими формулами використовуючи в якості вихідних даних значення нових змінних. Для оцінки адекватності нелінійної парної регресії спостережуваним даним можна використовувати критерій Фішера. Перевірка виконується за таким же алгоритмом, що й для лінійної парної регресії.
Довірчі межі прогнозу для квазілінійної парної регресії оцінюються за тими ж формулами, що й для лінійної парної регресії, лише замість х розглядають х/ . Інтервальний прогноз індивідуального значення при заданому рівні значимості α = 0,05 для yn+1 знаходять за формулою:
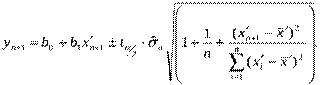
Інтервал довіри для математичного сподівання yn+1 :
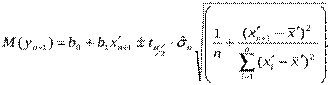
У тих випадках, коли нелінійна регресія перетворюється в лінійну шляхом логарифмування і заміни змінних, довірча інтервальний прогноз знаходять для відповідної лінійної регресії, а потім, використовуючи зворотні перетворення для меж інтервалів довіри прогнозу лінійної регресії, знаходять межі інтервалів довіри прогнозу нелінійної регресії.





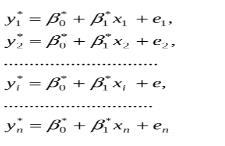
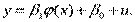 Заміною величин
Заміною величин 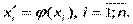 нелінійна парна регресія приводиться до лінійної парної регресії:
нелінійна парна регресія приводиться до лінійної парної регресії:  Формули для оцінок параметрів набувають вигляду
Формули для оцінок параметрів набувають вигляду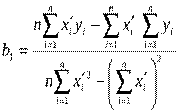 ,
, 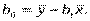
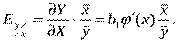 Для оцінки коефіцієнта еластичності нелінійної регресії в загальному використовується формула:
Для оцінки коефіцієнта еластичності нелінійної регресії в загальному використовується формула: 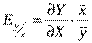 , де
, де 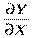 - частинна похідна функції у за змінною х.
- частинна похідна функції у за змінною х.