Математичним сподіванням дискретної випадкової величини , яка набуває значень із скінченної множини чисел , називається число
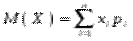
яке дорівнює сумі добутків значень випадкової величини на відповідні ймовірності.
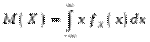 Математичним сподіванням неперервної випадкової величини , яка має щільність розподілу , називається число
Математичним сподіванням неперервної випадкової величини , яка має щільність розподілу , називається число
Математичне сподівання випадкової величини має такі властивості.
1.Математичне сподівання сталої випадкової величини дорівнює цій величині.(Мс = с, де с = const).
2.Математичне сподівання суми двох випадкових величин дорівнює сумі їх математичних сподівань. (M(X + Y) = MX + MY).
3.Математичне сподівання добутку двох незалежних випадкових величин дорівнює добутку їх математичних сподівань. (M(X × Y)=MX × MY).
4.Сталу величину можна виносити за знак математичного сподівання. (M(сX) = сMX, де с = const).
5.Математичне сподівання відхилення випадкової величини від свого математичного сподівання дорівнює нулеві. (М(Х – МХ) = 0).
Дайте означення функції розподілу ВВ.
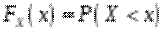 Функцією розподілу ймовірностей довільної випадкової величини або просто функцією розподілу величини називається функція, яка представляє розподіл величини : значення цієї функції в точці
Функцією розподілу ймовірностей довільної випадкової величини або просто функцією розподілу величини називається функція, яка представляє розподіл величини : значення цієї функції в точці 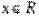 дорівнює ймовірності того, що випадкова величина набуває значення менше :
дорівнює ймовірності того, що випадкова величина набуває значення менше :
Оскільки функція розподілу являє собою ймовірність, вона повинназадовольняти основним аксіомам теорії ймовірностей і мати властивості, притаманні ймовірностям. Але ця функція залежить від можливих значень випадкової величини , і тому повинна в загальному вигляді визначатися для всіх значень . Таким чином, вимога, щоб функція розподілу являла собою ймовірність, накладає на її властивості певні обмеження.
Основні властивості функції розподілу довільної випадкової величини :
1) 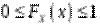 ,
, 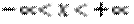 ;
;
2) 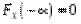 ,
, 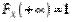 (
( 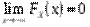 ,
, 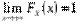 )
)
3) Функція не зменшується при зростанні (неспадна, тобто 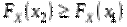 , якщо
, якщо 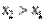 .)
.)
4) 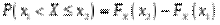 .
.
Відзначимо ще одну властивість функції 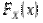 :
:
5) Якщо 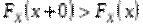 , то
, то
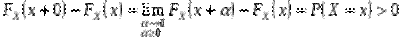 ,
,
тобто стрибок функції в довільній точці 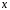 збігається з ймовірністю події
збігається з ймовірністю події 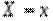 .
.





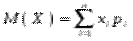
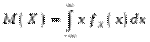 Математичним сподіванням неперервної випадкової величини , яка має щільність розподілу , називається число
Математичним сподіванням неперервної випадкової величини , яка має щільність розподілу , називається число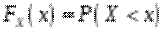 Функцією розподілу ймовірностей довільної випадкової величини або просто функцією розподілу величини називається функція, яка представляє розподіл величини : значення цієї функції в точці
Функцією розподілу ймовірностей довільної випадкової величини або просто функцією розподілу величини називається функція, яка представляє розподіл величини : значення цієї функції в точці 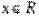 дорівнює ймовірності того, що випадкова величина набуває значення менше :
дорівнює ймовірності того, що випадкова величина набуває значення менше :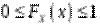 ,
, 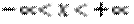 ;
;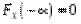 ,
, 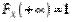 (
( 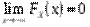 ,
, 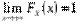 )
)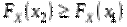 , якщо
, якщо 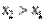 .)
.)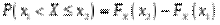 .
.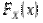 :
: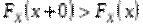 , то
, то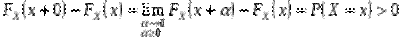 ,
,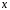 збігається з ймовірністю події
збігається з ймовірністю події 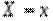 .
.


