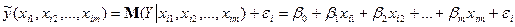Регресі́йний ана́ліз — розділ математичної статистики, присвячений методам аналізу залежності однієї величини від іншої. На відміну від кореляційного аналізу не з'ясовує чи істотний зв'язок, а займається пошуком моделі цього зв'язку, вираженої у функції регресії.
Регресійний аналіз використовується в тому випадку, якщо відношення між змінними можуть бути виражені кількісно у виді деякої комбінації цих змінних. Отримана комбінація використовується для передбачення значення, що може приймати цільова (залежна) змінна, яка обчислюється на заданому наборі значень вхідних (незалежних) змінних. У найпростішому випадку для цього використовуються стандартні статистичні методи, такі як лінійна регресія. На жаль, більшість реальних моделей не вкладаються в рамки лінійної регресії. Наприклад, розміри продажів чи фондові ціни дуже складні для передбачення, оскільки можуть залежати від комплексу взаємозв'язків множин змінних. Таким чином, необхідні комплексні методи для передбачення майбутніх значень.
Мета регресійного аналізу
Визначення ступеня детермінованості варіації критеріальної (залежної) змінної предикторами (незалежними змінними).
Прогнозування значення залежної змінної за допомогою незалежної.
Визначення внеску окремих незалежних змінних у варіацію залежної.
Регресійний аналіз не можна використовувати для визначення наявності зв'язку між змінними, оскільки наявність такого зв'язку і є передумова для застосування аналізу.
Теоретичне, емпіричне рівняння багатофакторної регресії.
На будь-який економічний показник найчастіше впливає не один, а декілька факторів. У цьому випадку замість парної регресії розглядається багатофакторна регресія:
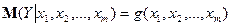 (1)
(1)
Рівняння багатофакторної регресії може бути представлене у вигляді:
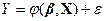 (2)
(2)
де 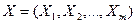 – вектор незалежних (пояснюючих) змінних;
– вектор незалежних (пояснюючих) змінних;
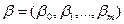 – вектор невідомих параметрів;
– вектор невідомих параметрів;
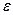 – випадкове відхилення;
– випадкове відхилення;
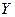 – залежна (пояснювана) змінна.
– залежна (пояснювана) змінна.
Розглянемо найбільш просту з моделей багатофакторної регресії – модель багатофакторної лінійної регресії.
Теоретичне лінійне рівняння багатофакторної регресії має вигляд:
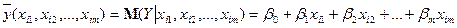 (3)
(3)
Фактичні значення залежної змінної знаходяться за формулою:
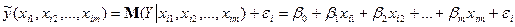





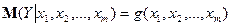 (1)
(1)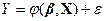 (2)
(2)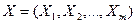 – вектор незалежних (пояснюючих) змінних;
– вектор незалежних (пояснюючих) змінних;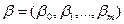 – вектор невідомих параметрів;
– вектор невідомих параметрів;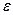 – випадкове відхилення;
– випадкове відхилення;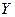 – залежна (пояснювана) змінна.
– залежна (пояснювана) змінна.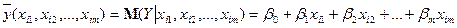 (3)
(3)