Однією із сфер застосування бінарних змінних є аналіз сезонних коливань. За допомогою цих змінних можна усунути сезонні коливання з метою визначення головних тенденцій розвитку певного економічного процесу.
Приклад 9.2. Нехай y — обсяг споживання певного продукту, який залежить від пори року. Для виявлення сезонності можна ввести
бінарні змінні d1, d2, d3:
d1 — 1, якщо місяць року зимовий, d1 — 0 — в інших випадках;
d2 — 1, якщо місяць року весняний, d2 — 0 — в інших випадках;
d3 — 1, якщо місяць року літній, d3 — 0 — в інших випадках.
На базі відповідних статистичних даних методом найменших квадратів можна оцінити параметри a3 лінійного регресійного рівняння
y — a0 + a d1 + a2 d2 + a3d3 + u.
Отримані результати мають такий зміст: коефіцієнт a0 визначає середньомісячний обсяг споживання досліджуваного продукту; суми коефіцієнтів a0 + a0 + a0 + a3 — обсяг споживання відповідно взимку, навесні та влітку. Отже, параметри a3 вказують на сезонні відхилення в обсягах споживання продукту відносно осінніх місяців. Перевірка статистичної значущості кожного з коефіцієнтів регресії виконується за допомогою традиційного t-тесту. Прийняття гіпотези про рівність нулю кожного з параметрів означає несуттєву різницю між споживанням в осінній період і споживанням в інший сезон. Комплексна гіпотеза a — a2 — a3 — 0 перевіряється за допомогою Р-тесту. Зокрема, якщо приймається припущення a — то це означає, що споживання взимку та весною не відрізняються між собою і т. ін.
Виявлення автокореляції за допомогою графічного методу, методу рядів.
Графічний метод
Існує кілька варіантів графічного визначення автокореляції. Відповідно до одному з них, на графіку відбиваються відхилення 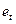 , що відповідають моментам
, що відповідають моментам 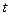 . Це так називані послідовно-часові графіки. На рис.1 наведені приклади послідовно-часових графіків.
. Це так називані послідовно-часові графіки. На рис.1 наведені приклади послідовно-часових графіків.
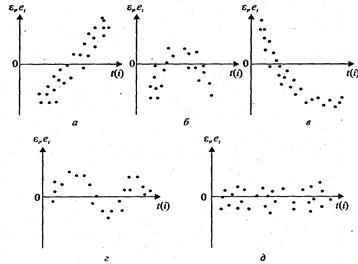
Рис. 1
У випадку, якщо на графіку є визначені зв'язки між відхиленнями (рис. 1, а) – г), то автокореляція має місце. Відсутність залежності свідчить про відсутність автокореляції (рис. 1, д).
Метод рядів
Послідовно визначаються знаки відхилень 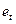 ,
, 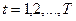 .
.
Наприклад, 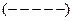
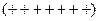
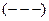
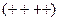
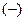 , тобто 5 «-», 7 «+», 3 «-», 4 «+», 1 «-» при 20 спостереженнях.
, тобто 5 «-», 7 «+», 3 «-», 4 «+», 1 «-» при 20 спостереженнях.
Візуальний розподіл знаків свідчить про невипадковий характер зв'язків між відхиленнями.
Виявлення гетероскедастичності (графічний аналіз залишків, тест рангової кореляції Спірмена).
Графічний аналіз залишків
При використанні методу графічного аналізу залишків по осі абсцис відкладаються значення ( 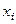 ) пояснюючої змінної
) пояснюючої змінної 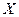 (або лінійної комбінації пояснюючих змінних
(або лінійної комбінації пояснюючих змінних 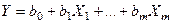 ), а по осі ординат або відхилення
), а по осі ординат або відхилення 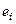 , або їх квадрати
, або їх квадрати 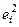 ,
, 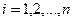 .
.
Приклади цих графіків наведені на рис. 4.– 8.
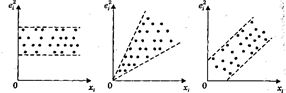
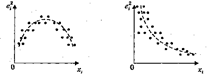
На рис. 4 усі відхилення 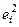 знаходяться усередині смуги постійної ширини, що паралельна осі абсцис. Це говорить про незалежність дисперсій
знаходяться усередині смуги постійної ширини, що паралельна осі абсцис. Це говорить про незалежність дисперсій 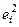 від значень змінної
від значень змінної 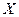 і їхній сталості, тобто в цьому випадку виконується умова гомоскедастичності. Ситуації, що представлені на рис. 5 – 8 відбивають велику ймовірність наявності гетероскедастичності.Тест рангової кореляції Спірмена.Алгоритм тесту рангової кореляції Спірмена:
і їхній сталості, тобто в цьому випадку виконується умова гомоскедастичності. Ситуації, що представлені на рис. 5 – 8 відбивають велику ймовірність наявності гетероскедастичності.Тест рангової кореляції Спірмена.Алгоритм тесту рангової кореляції Спірмена:
1) значення 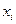 і
і 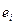 , ранжуються (упорядковуються по величинах).
, ранжуються (упорядковуються по величинах).
2) визначається коефіцієнт рангової кореляції: 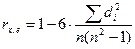 (1)
(1)
де 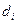 – різниця між рангами
– різниця між рангами 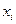 і
і 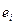 ,
, 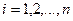 ;
; 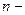 число спостережень.
число спостережень.
3) перевіряється значущість коефіцієнта рангової кореляції за допомогою t - критерію Стьюдента: 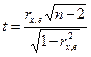 (2)
(2)
У випадку, якщо 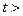
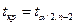 , то спостерігається гетероскедастичність, якщо
, то спостерігається гетероскедастичність, якщо 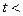
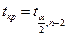 – гомоскедастичність.
– гомоскедастичність.
10. Дайте означення дисперсії ВВ.
Диспе́рсія є мірою відхилення значень випадкової величини від центру розподілу. Більші значення дисперсії свідчать про більші відхилення значень випадкової величини від центру розподілу.
Дисперсією випадкової величини X називається математичне сподівання квадрату відхилення від її математичного сподівання D(X) = M[X—N(X)]
Дисперсію зручніше обчислювати за формулою: D(X ) = M(X2)–[M(X)]2.
Властивості дисперсії.
Вастивість 1. Дисперсія постійної величини дорівнює нулю D(С)=0
Вастивість 2. Постійний множник виноситься за знак дисперсії, якщо піднести його до квадрату, тобто: D(СX)=С2 D(X)
Властивість 3. Дисперсія суми скінченої кількості незалежних випадкових величин дорівнює сумі дисперсій цих величин: D(x1 + x2+...+xn) = D(x1)+ D(x2)+..+ D(xn).
сперсія біноміального розподілу дорівнює добутку числа випробувань на ймовірності появи і не появленні події в одному випробуванні: D(X) = npq.
Середнє квадратичне відхилення. Середнім квадратичним відхиленням випадкової величину називають квадратний корінь з дисперсії: δ(Х)= 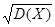 .
.





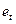 , що відповідають моментам
, що відповідають моментам 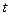 . Це так називані послідовно-часові графіки. На рис.1 наведені приклади послідовно-часових графіків.
. Це так називані послідовно-часові графіки. На рис.1 наведені приклади послідовно-часових графіків.
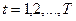 .
.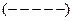
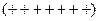
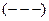
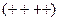
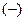 , тобто 5 «-», 7 «+», 3 «-», 4 «+», 1 «-» при 20 спостереженнях.
, тобто 5 «-», 7 «+», 3 «-», 4 «+», 1 «-» при 20 спостереженнях.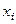 ) пояснюючої змінної
) пояснюючої змінної 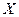 (або лінійної комбінації пояснюючих змінних
(або лінійної комбінації пояснюючих змінних 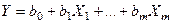 ), а по осі ординат або відхилення
), а по осі ординат або відхилення 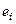 , або їх квадрати
, або їх квадрати 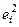 ,
,  .
.

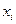 і
і 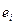 , ранжуються (упорядковуються по величинах).
, ранжуються (упорядковуються по величинах).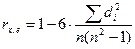 (1)
(1) 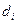 – різниця між рангами
– різниця між рангами 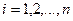 ;
; 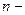 число спостережень.
число спостережень.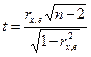 (2)
(2)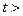
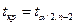 , то спостерігається гетероскедастичність, якщо
, то спостерігається гетероскедастичність, якщо 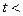
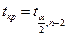 – гомоскедастичність.
– гомоскедастичність.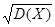 .
.

