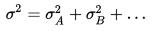Розглянемо існуючі методи усунення мультиколінеарності:
1. Виключення змінної(их) з моделі. Цей метод полягає в тому, що високо корельовано пояснюючі змінні видаляються з регресії, та вона заново оцінюється. Відбір змінних, що підлягають виключенню, виконується за допомогою коефіцієнта кореляції. Для цього розраховується оцінка значимості коефіцієнтів парної кореляції rij між пояснюючими змінними xi та xj. Досвід свідчить, що якщо |rij|>0.85, то одну з змінних можна виключити. Але яку змінну видалити з аналізу, вирішують виходячи з економічних міркувань.
2. Покрокова регресія. В аналіз послідовно додається по одній пояснюючій змінній. На кожному кроці перевіряється значимість коефіцієнтів регресії та оцінюється мультиколінеарність змінних. Якщо оцінка коефіцієнта отримується не значимою, то змінна виключається та розглядають іншу пояснюючу змінну. Якщо оцінка коефіцієнта кореляції значима, а мулько лінеарність відсутня, то ця змінна залишається і в аналіз включають наступну змінну. Таким чином, поступово визначають всі змінні, що складають регресію без порушення передумови про відсутність мультиколінеарності.
3. Зміна специфікації моделі: або змінюється форма моделі, або додаються пояснюючі змінні, не враховані в первісній моделі, але істотно впливають на залежну змінну.
4. Використання попередньої інформації про деякі параметри. Зазвичай на основі раніше проведеного регресійного аналізу або в результаті економічних досліджень вже є більш або менш точне уявлення про величину або співвідношення двох або декількох коефіцієнтів регресії. Ця попередня або не вибіркова інформація може бути використана дослідником при побудові регресії. У зв’язку з тим.., що частина оцінок, отримана на основі не вибіркових даних, вже має достатньо чітку інтерпретацію. Це полегшує шлях знаходження взаємних впливів змін різних змінних.
5. Перетворення змінних. У ряді випадків мінімізувати або взагалі усунути проблему мультиколінеарності можна за допомогою перетворення змінних.
Моделі ANCOVA
Моделі, у яких пояснюючі змінні носять як кількісний, так і якісний характер, називаються ANСOVA – моделями.
Спочатку розглянемо найпростішу ANСOVA – модель з однією кількісною й однією якісною змінною, що та має два альтернативних стани:
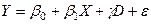 (2)
(2)
Нехай, наприклад, 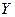 – заробітна плата співробітника фірми,
– заробітна плата співробітника фірми, 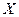 – стаж співробітника,
– стаж співробітника, 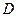 – стать співробітника, тобто
– стать співробітника, тобто
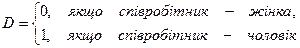
Тоді очікуване значення заробітної плати співробітників при 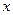 роках виробничого стажу буде:
роках виробничого стажу буде:
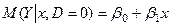 – для жінки, (3)
– для жінки, (3)
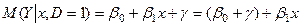 – для чоловіка. (4)
– для чоловіка. (4)
Якщо якісна змінна має 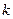 альтернативних значень, то при моделюванні використовуються тільки
альтернативних значень, то при моделюванні використовуються тільки 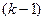 фіктивних змінних. Якщо не застосовувати це правило, то при моделюванні дослідник попадає в ситуацію досконалої мультиколінеарності.
фіктивних змінних. Якщо не застосовувати це правило, то при моделюванні дослідник попадає в ситуацію досконалої мультиколінеарності.
Значення фіктивної змінної можна змінювати на протилежні.
Значення якісної змінної, для якого приймається 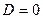 , називається базовим. Вибір базового значення звичайно диктується цілями дослідження, але може бути і довільним.
, називається базовим. Вибір базового значення звичайно диктується цілями дослідження, але може бути і довільним.
Коефіцієнт 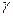 у моделі (2) іноді називається диференціальним коефіцієнтом вільного члена, тому що він показує, на яку величину відрізняється вільний член моделі при значенні фіктивній змінної рівної одиниці, від вільного члена моделі при базовому значенні фіктивної змінної.
у моделі (2) іноді називається диференціальним коефіцієнтом вільного члена, тому що він показує, на яку величину відрізняється вільний член моделі при значенні фіктивній змінної рівної одиниці, від вільного члена моделі при базовому значенні фіктивної змінної.
Нехай розглядається модель із двома пояснюючими змінними, одна з яких кількісна, а інша – якісна. Причому якісна змінна має три альтернативи. Наприклад, витрати на утримання дитини можуть бути зв'язані з доходами сімей і віком дитини: дошкільний, молодший шкільний і старший шкільний. Якісна змінна зв'язана з трьома альтернативами, тому за загальним правилом моделювання необхідно використовувати дві фіктивні змінні. Таким чином, модель може бути представлена у вигляді:
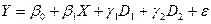 (5)
(5)
де 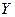 – витрати,
– витрати, 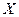 – доходи сімей.
– доходи сімей.
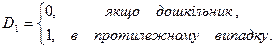
Утворяться наступні залежності. Середня витрата на дошкільника:
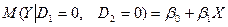 (6)
(6)
Середні витрати на молодшого школяра:
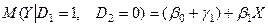 (7)
(7)
Середні витрати на старшого школяра:
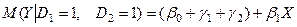 (8)
(8)
де 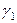 ,
, 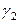 – диференціальні вільні члени. Базовим значенням якісної змінної є значення “дошкільник”.
– диференціальні вільні члени. Базовим значенням якісної змінної є значення “дошкільник”.
Після обчислення коефіцієнтів рівнянь регресії (6) – (8) визначається статистична значущість коефіцієнтів 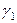 і
і 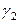 на основі звичайної
на основі звичайної 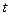 -статистики.
-статистики.
Якщо коефіцієнти 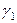 і
і 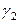 виявляються статистично незначущими, то можна зробити висновок, що вік дитини не впливає на витрати по його утриманню.
виявляються статистично незначущими, то можна зробити висновок, що вік дитини не впливає на витрати по його утриманню.
Моделі ANOVA.
Дисперсійний аналіз ( ANOVA ) являє собою статистичний метод аналізу результатів, які залежать від якісних ознак.
Кожен фактор може бути дискретною чи неперервною випадковою змінною, яку розділяють на декілька сталих рівнів (градацій, інтервалів). Якщо кількість вимірювань (проб, даних) на всіх рівнях кожного з факторів однакова, то дисперсійний аналіз називають рівномірним, інакше -нерівномірним.
В основі дисперсійного аналізу є такий принцип (факт з математичної статистики): якщо на випадкову величину діють взаємно незалежні фактори A, B, …, то загальна дисперсія дорівнює сумі дисперсій, зумовлених дією окремо кожного з факторів:
{\displaystyle \sigma ^{2}=\sigma _{A}^{2}+\sigma _{B}^{2}+\ldots } 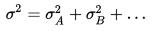
Дисперсійний аналіз полягає у виділенні й оцінюванні окремих факторів, що викликають зміну досліджуваної випадкової величини. При цьому проводиться розклад сумарної вибіркової дисперсії на складові, обумовлені незалежними факторами. Кожна з цих складових є оцінкою дисперсії генеральної сукупності. Щоб дати оцінку дієвості впливу даного фактору, необхідно оцінити значимість відповідної вибіркової дисперсії у порівнянні з дисперсією відтворення, обумовленою випадковими факторами. Перевірка значимості оцінок дисперсії проводять з допомогою критерію Фішера.
Коли розрахункове значення критерію Фішера виявиться меншим табличного, то вплив досліджуваного фактору немає підстав вважати значимим. Коли ж розрахункове значення критерію Фішера виявиться більшим табличного, то цей фактор впливає на зміни середніх. В подальшому ми вважаємо, що виконуються наступні припущення:
1. Випадкові помилки спостережень мають нормальний розподіл.
2. Фактори впливають тільки на зміну середніх значень, а дисперсія спостережень залишається постійною.
Фактори, що розглядаються в дисперсійному аналізі, бувають трьох родів:
· з випадковими рівнями, коли вибір рівнів проходить з безмежної сукупності можливих рівнів та супроводжується рандомізацією і рівні вибираються випадковим чином;
· з фіксованими рівнями;
· змішаного типу — частина факторів розглядається на фіксованих рівнях, але рівні решти вибираються випадковим чином.





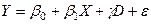 (2)
(2)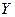 – заробітна плата співробітника фірми,
– заробітна плата співробітника фірми, 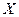 – стаж співробітника,
– стаж співробітника, 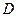 – стать співробітника, тобто
– стать співробітника, тобто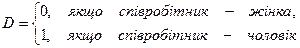
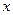 роках виробничого стажу буде:
роках виробничого стажу буде: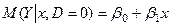 – для жінки, (3)
– для жінки, (3)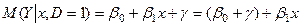 – для чоловіка. (4)
– для чоловіка. (4)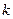 альтернативних значень, то при моделюванні використовуються тільки
альтернативних значень, то при моделюванні використовуються тільки 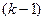 фіктивних змінних. Якщо не застосовувати це правило, то при моделюванні дослідник попадає в ситуацію досконалої мультиколінеарності.
фіктивних змінних. Якщо не застосовувати це правило, то при моделюванні дослідник попадає в ситуацію досконалої мультиколінеарності.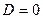 , називається базовим. Вибір базового значення звичайно диктується цілями дослідження, але може бути і довільним.
, називається базовим. Вибір базового значення звичайно диктується цілями дослідження, але може бути і довільним.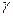 у моделі (2) іноді називається диференціальним коефіцієнтом вільного члена, тому що він показує, на яку величину відрізняється вільний член моделі при значенні фіктивній змінної рівної одиниці, від вільного члена моделі при базовому значенні фіктивної змінної.
у моделі (2) іноді називається диференціальним коефіцієнтом вільного члена, тому що він показує, на яку величину відрізняється вільний член моделі при значенні фіктивній змінної рівної одиниці, від вільного члена моделі при базовому значенні фіктивної змінної.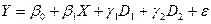 (5)
(5)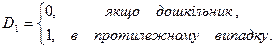
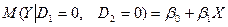 (6)
(6)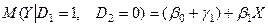 (7)
(7)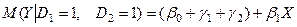 (8)
(8)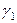 ,
, 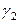 – диференціальні вільні члени. Базовим значенням якісної змінної є значення “дошкільник”.
– диференціальні вільні члени. Базовим значенням якісної змінної є значення “дошкільник”.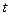 -статистики.
-статистики.