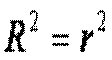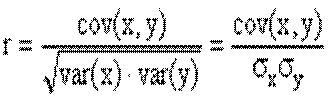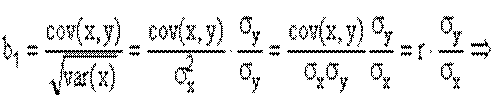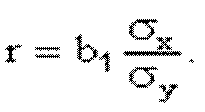Поряд з коефіцієнтом кореляції використовується ще один критерій, за допомогою якого також вимірюється щільність зв'язку між двома або більше показниками та перевіряється адекватність (відповідність) побудованої регресійної моделі реальній дійсності. Тобто дається відповідь на запитання, чи дійсно зміна значення у лінійно залежить саме від зміни значення х, а не відбувається під впливом різних випадкових факторів. Таким критерієм є коефіцієнт детермінації.
Щоб пояснити, що саме являє собою коефіцієнт детермінації та як він пов'язаний з коефіцієнтом кореляції, розглянемо питання про декомпозицію дисперсій.
Розглянемо на рисункі, як розбиваються на дві частини відхилення фактичних (емпіричних) значень залежної змінної від значень, які знаходяться на регресійній прямій (теоретичних 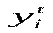 або розрахункових
або розрахункових 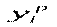 ):
):
Як видно із рисунка: 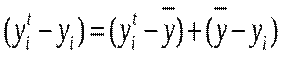 . Звідси дістаємо
. Звідси дістаємо
 . (*)
. (*)
В статистиці різницю  прийнято називати загальним відхиленням. Різницю
прийнято називати загальним відхиленням. Різницю  називають відхиленням, яке можна пояснити, виходячи із регресійної прямої. Різницю
називають відхиленням, яке можна пояснити, виходячи із регресійної прямої. Різницю  називають відхиленням, яке не можна пояснити, виходячи з регресійної прямої, або непояснюваним відхиленням. Піднесемо обидві частини (*) до квадрату і підсумуємо по. Враховуючи, що сума похибок дорівнює нулю, дістанемо:
називають відхиленням, яке не можна пояснити, виходячи з регресійної прямої, або непояснюваним відхиленням. Піднесемо обидві частини (*) до квадрату і підсумуємо по. Враховуючи, що сума похибок дорівнює нулю, дістанемо: 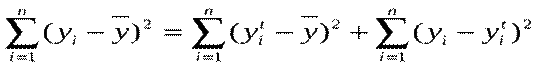 , (**)
, (**)
Поділивши обидві частини (*) на , отримаємо так зване «правило складання дисперсій»:
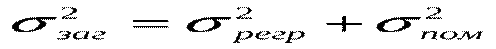 ,(***) Таким чином, ми розклали загальну дисперсію на дві частини: дисперсію, що пояснює регресію, та дисперсію помилок (або дисперсію випадкової величини). Поділимо обидві частини (***) на
,(***) Таким чином, ми розклали загальну дисперсію на дві частини: дисперсію, що пояснює регресію, та дисперсію помилок (або дисперсію випадкової величини). Поділимо обидві частини (***) на 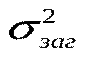 і отримаємо:
і отримаємо:
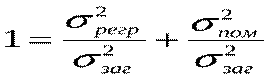 Як видно, перше відношення у правій частині є пропорцією дисперсії, що пояснює регресію, у загальній дисперсії. Друге відношення є пропорцією дисперсії помилок у загальній дисперсії, тобто є частиною дисперсії, яку не можна пояснити через регресійний зв’язок.
Як видно, перше відношення у правій частині є пропорцією дисперсії, що пояснює регресію, у загальній дисперсії. Друге відношення є пропорцією дисперсії помилок у загальній дисперсії, тобто є частиною дисперсії, яку не можна пояснити через регресійний зв’язок.
Частина дисперсії, що пояснює регресію, називається коефіцієнтом детермінації і позначається 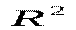 . Коефіцієнт детермінації використовується як критерій адекватності моделі, оскільки є мірою пояснювальної сили незалежної змінної . Коефіцієнт детермінації можна записати в одному із двох еквівалентних виразів:
. Коефіцієнт детермінації використовується як критерій адекватності моделі, оскільки є мірою пояснювальної сили незалежної змінної . Коефіцієнт детермінації можна записати в одному із двох еквівалентних виразів:
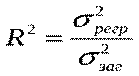 або
або 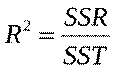 .
. 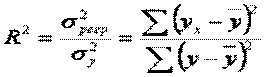 Очевидно, що
Очевидно, що 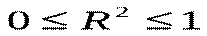 . Враховуючи, що коефіцієнт кореляції
. Враховуючи, що коефіцієнт кореляції 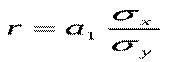 , неважко встановити наступний зв’язок між коефіцієнтами детермінації та кореляції (для лінійної регресії):
, неважко встановити наступний зв’язок між коефіцієнтами детермінації та кореляції (для лінійної регресії): 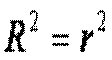
Отже коефіцієнт детермінації дорівнює квадрату коефіцієнта кореляції.
18. Зв’язок між коефіцієнтом кореляції та кутовим коефіцієнтом b1.
Який зв’язок існує між коефіцієнтом кореляції і нахилом прямої регресії b1. Нагадаємо, що: 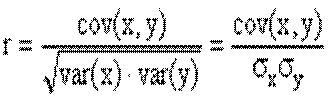
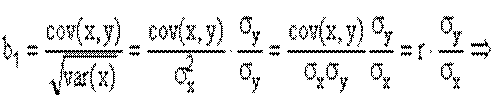
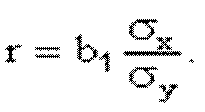
Так як значення додатні, то знак коефіцієнта кореляції завжди збігається із знаком параметра b1. Знак коефіцієнта кореляції співпадає із знаком коефіцієнта b1 в рівнянні регресії. Коефіцієнт кореляції знаходиться в межах від 0 до ±1. Якщо коефіцієнт кореляції дорівнює нулю, то зв'язок відсутній, а якщо одиниці, то зв'язок функціональний. Знак при коефіцієнті кореляції вказує на напрям зв'язку ("+" - прямий, "-" - обернений). Знак коефіцієнта показує "напрямок" зв'язку. Додатний коефіцієнт кореляції (r > 0) свідчить про "прямий" зв'язок між ознаками (тобто такий, коли збільшення значення однієї ознаки збільшує значення іншої ознаки), а від'ємний (г < 0) — про "зворотний" зв'язок (такий, коли зростання однієї ознаки веде до зменшення іншої ознаки). Чим ближче коефіцієнт кореляції до одиниці, тим зв'язок між ознаками тісніший.





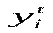 або розрахункових
або розрахункових 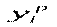 ):
):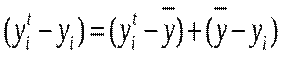 . Звідси дістаємо
. Звідси дістаємо . (*)
. (*) прийнято називати загальним відхиленням. Різницю
прийнято називати загальним відхиленням. Різницю  називають відхиленням, яке можна пояснити, виходячи із регресійної прямої. Різницю
називають відхиленням, яке можна пояснити, виходячи із регресійної прямої. Різницю  називають відхиленням, яке не можна пояснити, виходячи з регресійної прямої, або непояснюваним відхиленням. Піднесемо обидві частини (*) до квадрату і підсумуємо по. Враховуючи, що сума похибок дорівнює нулю, дістанемо:
називають відхиленням, яке не можна пояснити, виходячи з регресійної прямої, або непояснюваним відхиленням. Піднесемо обидві частини (*) до квадрату і підсумуємо по. Враховуючи, що сума похибок дорівнює нулю, дістанемо: 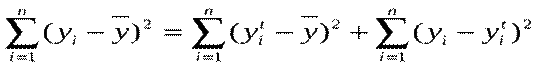 , (**)
, (**) 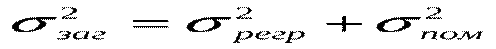 ,(***) Таким чином, ми розклали загальну дисперсію на дві частини: дисперсію, що пояснює регресію, та дисперсію помилок (або дисперсію випадкової величини). Поділимо обидві частини (***) на
,(***) Таким чином, ми розклали загальну дисперсію на дві частини: дисперсію, що пояснює регресію, та дисперсію помилок (або дисперсію випадкової величини). Поділимо обидві частини (***) на 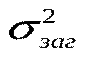 і отримаємо:
і отримаємо: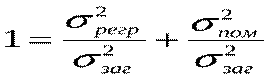 Як видно, перше відношення у правій частині є пропорцією дисперсії, що пояснює регресію, у загальній дисперсії. Друге відношення є пропорцією дисперсії помилок у загальній дисперсії, тобто є частиною дисперсії, яку не можна пояснити через регресійний зв’язок.
Як видно, перше відношення у правій частині є пропорцією дисперсії, що пояснює регресію, у загальній дисперсії. Друге відношення є пропорцією дисперсії помилок у загальній дисперсії, тобто є частиною дисперсії, яку не можна пояснити через регресійний зв’язок.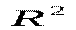 . Коефіцієнт детермінації використовується як критерій адекватності моделі, оскільки є мірою пояснювальної сили незалежної змінної . Коефіцієнт детермінації можна записати в одному із двох еквівалентних виразів:
. Коефіцієнт детермінації використовується як критерій адекватності моделі, оскільки є мірою пояснювальної сили незалежної змінної . Коефіцієнт детермінації можна записати в одному із двох еквівалентних виразів: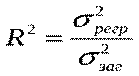 або
або 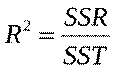 .
. 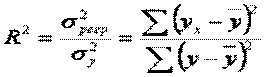 Очевидно, що
Очевидно, що 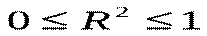 . Враховуючи, що коефіцієнт кореляції
. Враховуючи, що коефіцієнт кореляції 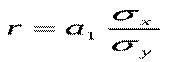 , неважко встановити наступний зв’язок між коефіцієнтами детермінації та кореляції (для лінійної регресії):
, неважко встановити наступний зв’язок між коефіцієнтами детермінації та кореляції (для лінійної регресії):