Для перевірки загальної якості рівняння багатофакторної регресії застосовують:
1. Коефіцієнт детермінації:
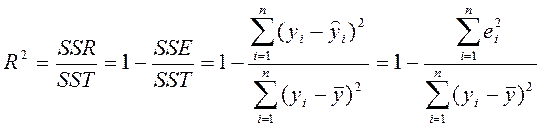 (12)
(12)
2. Скоригований коефіцієнт детермінації:
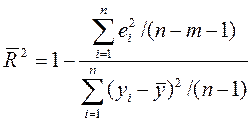 (13)
(13)
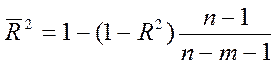 (14)
(14)
З (14) випливає, що 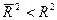 для
для 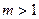 .
. 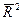 може бути і від’ємним.
може бути і від’ємним.
3. Індекс кореляції (множинний коефіцієнт кореляції) :
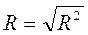 ,
, 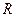 Î [0, 1]. (15)
Î [0, 1]. (15)
Для перевірки статистичної значущості коефіцієнта детермінації застосовують F-критерій Фішера. Аналіз статистичної значущості коефіцієнта детермінації проводять за наступними етапами:
1) розраховують F-статистику:
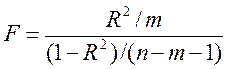 , (16)
, (16)
де 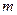 – кількість незалежних змінних;
– кількість незалежних змінних;
2) з таблиць критичних точок розподілу Фішера знаходять 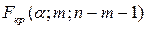 ;
;
3) якщо 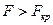 , то
, то 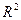 є статистично значущим, рівняння якісно описує зв’язок між залежною і незалежними змінними.
є статистично значущим, рівняння якісно описує зв’язок між залежною і незалежними змінними.
Визначення коефіцієнта детермінації для парної лінійної регресії.
Функціональна залежність умовного математичного сподівання 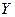 від
від 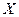 називається функцієюрегресії
називається функцієюрегресії 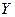 на
на 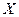 :
: 
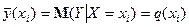 (1)
(1)
де 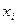 – значення ВВ
– значення ВВ 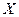 в
в 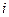 -му спостереженні,
-му спостереженні, 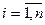 .
.
Парна лінійна регресія являє собою лінійну функцію між умовним математичним сподіванням 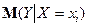 залежної змінної
залежної змінної 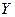 і однією незалежною змінною
і однією незалежною змінною 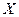 :
: 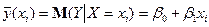 .(2)Співвідношення (2) називається теоретичним лінійним рівнянням регресії. Для відображення того факту, що кожне фактичне значення залежної змінної (
.(2)Співвідношення (2) називається теоретичним лінійним рівнянням регресії. Для відображення того факту, що кожне фактичне значення залежної змінної ( 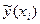 ) відхиляється від відповідного умовного математичного сподівання (
) відхиляється від відповідного умовного математичного сподівання ( 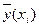 ), необхідно ввести в співвідношення випадковий доданок
), необхідно ввести в співвідношення випадковий доданок 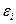 :
: 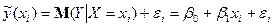 , (3)
, (3)
де 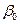 ,
, 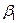 – теоретичні параметри (теоретичні коефіцієнти) регресії;
– теоретичні параметри (теоретичні коефіцієнти) регресії; 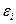 – випадкові відхилення.Співвідношення (3) називається теоретичною лінійною регресійною моделлю. За вибіркою можна побудувати емпіричне рівняння регресії:
– випадкові відхилення.Співвідношення (3) називається теоретичною лінійною регресійною моделлю. За вибіркою можна побудувати емпіричне рівняння регресії: 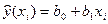 , (4)
, (4)
де 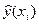 – оцінка умовного математичного сподівання
– оцінка умовного математичного сподівання 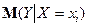 ;
;
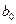 ,
, 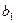 – оцінки невідомих параметрів
– оцінки невідомих параметрів 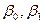 (емпіричні коефіцієнти регресії).
(емпіричні коефіцієнти регресії).
Фактичні значення залежної змінної ( 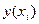 ) розраховуються за формулою:
) розраховуються за формулою:
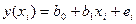 , (5)
, (5)
де 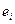 – оцінка теоретичного випадкового відхилення
– оцінка теоретичного випадкового відхилення 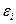 .
.





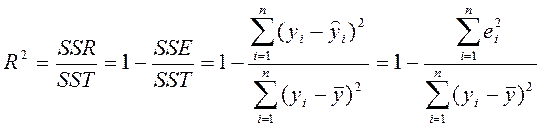 (12)
(12)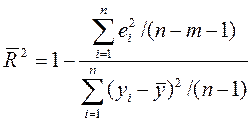 (13)
(13)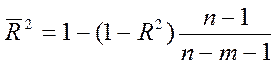 (14)
(14)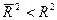 для
для 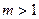 .
. 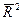 може бути і від’ємним.
може бути і від’ємним.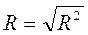 ,
, 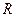 Î [0, 1]. (15)
Î [0, 1]. (15)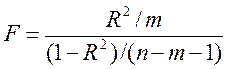 , (16)
, (16)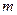 – кількість незалежних змінних;
– кількість незалежних змінних;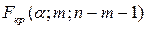 ;
;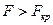 , то
, то  є статистично значущим, рівняння якісно описує зв’язок між залежною і незалежними змінними.
є статистично значущим, рівняння якісно описує зв’язок між залежною і незалежними змінними.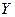 від
від 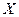 називається функцієюрегресії
називається функцієюрегресії 
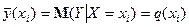 (1)
(1) 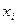 – значення ВВ
– значення ВВ 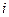 -му спостереженні,
-му спостереженні, 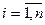 .
.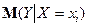 залежної змінної
залежної змінної 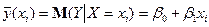 .(2)Співвідношення (2) називається теоретичним лінійним рівнянням регресії. Для відображення того факту, що кожне фактичне значення залежної змінної (
.(2)Співвідношення (2) називається теоретичним лінійним рівнянням регресії. Для відображення того факту, що кожне фактичне значення залежної змінної ( 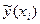 ) відхиляється від відповідного умовного математичного сподівання (
) відхиляється від відповідного умовного математичного сподівання ( 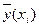 ), необхідно ввести в співвідношення випадковий доданок
), необхідно ввести в співвідношення випадковий доданок 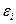 :
: 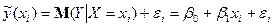 , (3)
, (3) 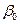 ,
, 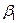 – теоретичні параметри (теоретичні коефіцієнти) регресії;
– теоретичні параметри (теоретичні коефіцієнти) регресії; 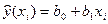 , (4)
, (4)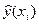 – оцінка умовного математичного сподівання
– оцінка умовного математичного сподівання 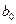 ,
, 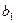 – оцінки невідомих параметрів
– оцінки невідомих параметрів 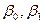 (емпіричні коефіцієнти регресії).
(емпіричні коефіцієнти регресії).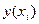 ) розраховуються за формулою:
) розраховуються за формулою: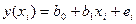 , (5)
, (5)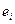 – оцінка теоретичного випадкового відхилення
– оцінка теоретичного випадкового відхилення 

