

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...
Топ:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Интересное:
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
На будь-який економічний показник найчастіше впливає не один, а декілька факторів. У цьому випадку замість парної регресії розглядається багатофакторна регресія:
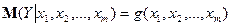 (1)
(1)
Рівняння багатофакторної регресії може бути представлене у вигляді:
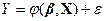 (2)
(2)
де 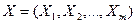 – вектор незалежних (пояснюючих) змінних;
– вектор незалежних (пояснюючих) змінних;
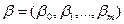 – вектор невідомих параметрів;
– вектор невідомих параметрів;
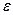 – випадкове відхилення;
– випадкове відхилення;
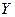 – залежна (пояснювана) змінна.
– залежна (пояснювана) змінна.
Розглянемо найбільш просту з моделей багатофакторної регресії – модель багатофакторної лінійної регресії.
Теоретичне лінійне рівняння багатофакторної регресії має вигляд:
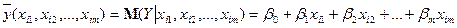 (3)
(3)
Фактичні значення залежної змінної знаходяться за формулою:
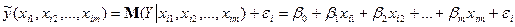 (4)
(4)
Сформулюйте означення парної лінійної регресії.
Функціональна залежність умовного математичного сподівання 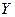 від
від 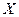 називається функцією регресії
називається функцією регресії 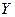 на
на 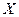 :
:

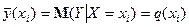 (1)
(1)
де 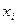 – значення ВВ
– значення ВВ 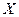 в
в 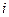 -му спостереженні,
-му спостереженні, 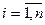 .
.
Парна лінійна регресія являє собою лінійну функцію між умовним математичним сподіванням 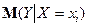 залежної змінної
залежної змінної 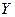 і однією незалежною змінною
і однією незалежною змінною 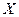 :
:
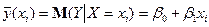 . (2)
. (2)
Співвідношення (2) називається теоретичним лінійним рівнянням регресії. Для відображення того факту, що кожне фактичне значення залежної змінної ( 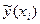 ) відхиляється від відповідного умовного математичного сподівання (
) відхиляється від відповідного умовного математичного сподівання ( 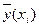 ), необхідно ввести в співвідношення (2) випадковий доданок
), необхідно ввести в співвідношення (2) випадковий доданок 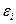 :
:
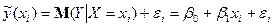 , (3)
, (3)
де 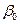 ,
, 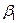 – теоретичні параметри (теоретичні коефіцієнти) регресії;
– теоретичні параметри (теоретичні коефіцієнти) регресії;
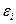 – випадкові відхилення.
– випадкові відхилення.
Співвідношення (3) називається теоретичною лінійною регресійною моделлю. За вибіркою можна побудувати емпіричне рівняння регресії:
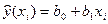 , (4)
, (4)
де 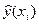 – оцінка умовного математичного сподівання
– оцінка умовного математичного сподівання 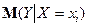 ;
;
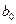 ,
, 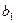 – оцінки невідомих параметрів
– оцінки невідомих параметрів 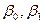 (емпіричні коефіцієнти регресії).
(емпіричні коефіцієнти регресії).
Фактичні значення залежної змінної ( 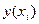 ) розраховуються за формулою:
) розраховуються за формулою:
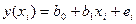 , (5)
, (5)
де 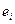 – оцінка теоретичного випадкового відхилення
– оцінка теоретичного випадкового відхилення 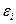 .
.
|
|
|

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!