Тезисы лекций и лабороторных занятий

ТЕЗИСЫ ЛЕКЦИЙ И ЛАБОРОТОРНЫХ ЗАНЯТИЙ

(на основе книги Пантелеева)

1 ИСТОРИЯ РАЗВИТИЯ МЕТОДОВ ОПТИМИЗАЦИИ И ОБЗОР КУРСА.. 3

1.1 Основные этапы развития теории оптимизации. 3

1.2 Обзор курса. 7

2 АЛГОРИТМЫ МЕТОДОВ ПОИСКА ЭКСТРЕМУМОВ.. 10

2.1 Классификация методов программирования. 10

2.2 Необходимые и достаточные условия безусловного экстремума (§ 20) 10

3 ТЕОРЕМА КУНА-ТАККЕРА.. 39

3.1. Предыстория: линейное программирование и принцип и метод Лагранжа. 39

3.2. Классификация задач нелинейного программирования. 41

3.3. Метод Лагранжа. 48

3.4. Банаховы и гильбертовы пространства. 51

3.5. Роль выпуклости. 52

3.6. Формулировка и доказательство теоремы Куна-Таккера. 53

Если непрерывная функция n переменных x = (x1,...,xn) F(х) имеет в точке х _опт максимум, то существует ε > 0 такое, что для всех x из ε-окрестности точки х _опт 55

3.7. Минимаксная трактовка задачи на условный экстремум.. 58

3.8. Минимаксная трактовка задачи на условный экстремум.. 63

3.9. Теорема Куна-Таккера. 69

3.10. Связь теоремы Куна-Таккера с теорией игр и седловыми точками. 72

ЛИТЕРАТУРА.. 74

ПРИЛОЖЕНИЕ.. 75

 

 

 

 

ИСТОРИЯ РАЗВИТИЯ МЕТОДОВ ОПТИМИЗАЦИИ И ОБЗОР КУРСА

Обзор курса

Обзор делается на основе оглавления книги. Примерно 14 занятий = 4 месяца х 4 занятия в месяц. Кратко характеризуются все пункты (главы (их 5) и параграфы (их 16)) курса. Теоретическая часть. Что будет на лабораторных занятиях.

Название курса определяет достаточно большую область прикладной математики. Широкую по охвату тем, богатую теоретическими методами и алгоритмами и имеющую большое практическое применение. Основные темы курса «Теория и методы оптимизации» хорошо отражены в книге Пантелеева и Летовой, на которой построен курс: и лекции и лабораторные работы (практические занятия). Скорее всего, наш курс сможет охватить только эти разделы, относящиеся к классическим основным методам:

- Глава 1 – необходимые и достаточные условия экстремума в простейшем случае гладких (дифференцируемых) функций;

- Глава 2, § 5.1 – численные методы безусловной одномерной оптимизации;

- Глава 2, §§ 4, 5.2-5.6, 6, 7 – численные методы безусловной многомерной (векторной) оптимизации;

- Глава 3 – численные методы поиска условного экстремума;

- Глава 4 – задачи линейного программирования;

- Глава 5 – задачи вариационного исчисления.

Как дальнейшее развитие темы примерно после 1940 года возникли следующие разделы, вызванные к жизни сложнейшими практическими задачами в технике и экономике.

Нелинейное программирование является естественным, но абсолютно нетривиальным обобщением линейного программирования. Эта тематика имеет и другие названия: экстремальные задачи, выпуклое программирование. Первоначально линейное программирование было создано Канторовичем для решения сложных экономических задач планирования. Методы нелинейного программирования применяются для намного большего класса задач как в фундаментальных научных исследованиях и инженерном деле, так и в экономике – на них построена вся современная теория планирования балансов предприятий и целых стран.

Теория управления или оптимального управления. Возникла как обобщение вариационного исчисления для решения задач управления движением в воздушном пространстве и космосе. В настоящее время применяется в сложных случаях при решениях сложных задач во многих отраслях техники и гуманитарных областях.

Внутри этих теорий были созданы такие подразделы, как теория игр, дифференциальные игры, многоэкстремальные задачи.

Была построена абстрактная теоретическая база методов оптимизации, охватывающая и обобщающая многие похожие задачи и случаи, на основе теории нормированных пространств и методов функционального анализа.

Мы до этого всего, из-за ограниченного времени курса (1 семестр) почти наверняка не дойдём и изучать не будем. Я решил лучше сосредоточиться на аккуратном изучении основ, чем на поверхностном ознакомлении с многочисленными темами и подтемами этой науки. Кроме того, акцент будет сделан на практические навыки решения задач, а не на их теоретическом обосновании. Хотя бы удовлетворительное владение этими навыками будет крайне полезно при решении практически любой научно-технической или инженерной задачи.

Лекции будут читаться по тексту книги на компьютере, лабораторные (или практические) работы также будут основаны на задачах из книги и будут состоять из 2-х или 3-х разделов (пока не знаю, будет ли третий раздел):

- аналитическое решение в тетради задач к разделам книги – там, где возможно разумное аналитическое решение, в основном это – одномерный случай (20-30 задач): задачи стр. 21 (все 8), задачи стр. 33 (все 10), задачи стр. 96 (5-6 штук);

- написание программ на Matlab (примерно 5 штук), реализующие векторные методы безусловной и условной оптимизации;

- написание программы на Matlab, решающей реальную несложную задачу методами глав 4 и 5 (если останется время).

Результаты лабораторных работ будут обеспечивать получение зачёта. Для получения стандартного задания необходимо посетить 50% занятий. В случае нарушения этого условия, для получения зачёта надо будет выполнить задание большее по объёму или сложности в 2-3 раза.

Экзамена не будет, если не поменяли с прошлого года.

ТЕОРЕМА КУНА-ТАККЕРА

Метод Лагранжа

Начнём рассмотрение задачи поиска экстремума функции с ограничениями равенствами с «метода множителей Лагранжа».

Алгоритм метода состоит из следующих шагов:

- составим функцию Лагранжа в виде линейной комбинации целевой функции и функций взятых с коэффициентами, называемыми множителями Лагранжа – : ; (3.2)

- будем считать все функции непрерывно дифференцируемыми и приравняем 0 градиент функции Лагранжа : ;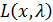

- составим систему n+m уравнений, состоящих из равенства 0 градиента и уравнений ограничений:

(3.3)

1. найдём решения этой системы уравнений, которые будут стационарными точками задачи – определяющими необходимые условия решения задачи поиска условного экстремума.

Рассмотрим эвристические геометрические рассуждения на плоскости, помогающие понять смысл метода. Для этого рассмотрим изображённый на рисунке двумерный случай:

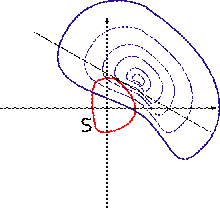
Рисунок 5.1 – Линии уровня целевой функции двух переменных f(x,y) и кривой ограничений g(x,y)

 

В двумерном случае имеем целевую функцию двух переменных 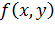при условии, задаваемом уравнением g . На рисунке изображены линии уровня функции 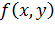(т.е. геометрическое место точек, где 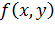=const) и кривую ограничений . Так как все функции непрерывно дифференцируемы, то и все кривые являются гладкими. Тогда задача сводится к нахождению экстремума функции f на кривой S. Будем также считать, что S не проходит через точки, в которых градиент целевой функции равен нулю: .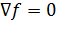

В точках, где кривая S трансверсальна (пересекает под ненулевым углом) линиям уровня, двигаясь по кривой S из этой точки можно попасть как на линии уровня, соответствующие большему значению, так и меньшему значения функции f. Следовательно, такая точка не может быть точкой экстремума, и стационарными точками являются такие точки, где кривые пересекаются под нулевым углом, т.е. их касательные параллельны и градиенты пропорциональны:

(3.4)

- некоторое число, отличное от нуля, являющееся множителем Лагранжа.

В общем многомерном случае условию аналогичному параллельности касательных является параллельность касательных плоскостей, которому также соответствует пропорциональность градиентов.

Рассмотрим регулярный случай, т.е. невырожденность градиента, и рассмотрим функцию Лагранжа, как зависящую также и от :

. (3.5)

Необходимым условием ее экстремума является равенство нулю градиента функции трёх переменных x, y, :

. (3.6)

В соответствии с правилами дифференцирования, оно записывается в виде равенства 0 частных производных по x, y и уравнения ограничения.

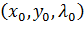Мы получили систему, первые два уравнения которой эквивалентны необходимому условию локального экстремума (1), а третье — уравнению g . Из нее можно найти . При этом 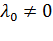, поскольку в противном случае градиент функции f обращается в нуль в точке 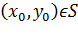, что противоречит нашим предположениям. Следует заметить, что найденные таким образом точки могут и не являться искомыми точками условного экстремума, ведь рассмотренное условие носит необходимый, но не достаточный характер. Нахождение условного экстремума с помощью вспомогательной функции и составляет основу метода множителей Лагранжа, примененного здесь для простейшего случая двух переменных. Оказывается, вышеприведенные рассуждения обобщаются на случай произвольного числа переменных и уравнений, задающих условия.

На основе метода множителей Лагранжа можно доказать и некоторые достаточные условия для условного экстремума, требующие анализа вторых производных функции Лагранжа.

Роль выпуклости

Выпуклым множеством называется такое множество, что для каждых двух точек этого множества каждая точка соединяющей их прямой также принадлежит этому множеству.

Соответственно, выпуклой функцией называется такая функция, что

. (3.2.1)

Рисунок 3.4.1 – Выпуклая функция

 

Покажем, что в случае соответствующей гладкости это эквивалентно трём другим свойствам выпуклой функции:

2. ; (3.2.2)

3. ; (3.2.3)

4. – выпуклая, для . (3.2.4)

Докажем эти свойства.

………………………………………..

Пусть f выпуклая и дифференцируемая. Разложим функцию в ряд Тейлора и отбросим малые выше второго порядка:

.

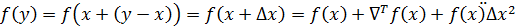Из выпуклости следует…….

 

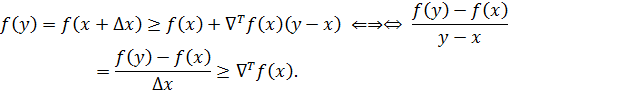
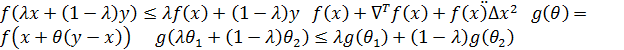
Итак, пусть выпукла.

Тогда ….

Тогда ….

Тогда являющаяся проекцией функции f на подпространство функция – также выпуклая:

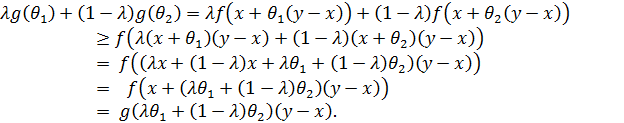
В обратную сторону, пусть ……..

……………………………………………………………..

Теорема Куна-Таккера

Формулы (3.8.2)-(3.8.7) составляют содержание теоремы Куна-Таккера, только в отличие от предыдущего параграфа, где функция была произвольной, в данном случае она является функцией Лагранжа для задачи максимизации нелинейного программирования, а (х_опт,λ_опт) - точка экстремума. Сама теорема может быть сформулирована следующим образом: соотношения (3.8.2)-(3.8.7) являются необходимыми и достаточными условиями, для того чтобы точка х_опт представляла собой решение задачи выпуклого нелинейного программирования:

max { F(x)|x_j≥0, j=1,...,n; φ_i(х)≤b_i, i = 1,...,m }. (3.8.29)

Сведем исходную задачу к классической постановке. Для этого прежде всего ограничения-неравенства φ_i(х)≥ b_i сведем к равенствам, введя и переменных x_φi ≥0 (i = 1,2,..., u), соответствующим неравенствам. Остальные m – u ограничений считаются строгими равенствами. Тогда

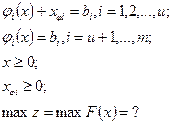(3.8.30)

Тем самым допускается, что часть из m неравенств имеет вид строгих равенств.

Предположим, что для этой задачи х = х_опт. Обозначим через J множество индексов j (j = 1,..., n) для которых x_jопт > 0, а через – множество индексов j, для которых x_jопт = 0. Аналогично будем считать, что I - множество индексов i (i = 1,..., u) для которых φ_i(х_oпт) = b_i, – множество, состоящее из индексов i, для которых ограничения на φ_i(х_опт) выполняются со знаком строгого неравенства φ_i(x_опт)< b_i. Заметим, что речь идет только о точке оптимума х_опт и знак нестрогого неравенства "≥" теряет свой смысл и соотношение превращается или в строгое неравенство (типа 5>4) или в строгое равенство (типа 3=3). На основании результатов, полученных в § 17-3, можем написать, что

(3.8.31)

так как множество J соответствует внутренней области допустимых значений, и λ_iопт = 0, , так как множество I соответствует ограничениям в виде строгих неравенств, которые можно не учитывать. Далее

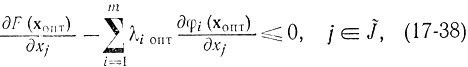(3.8.32)

так как множество J соответствует границе области допустимых значений.

Соотношения (3.8.31) и (3.8.32) обеспечивают выполнение условия (3.8.2)

(3.8.33)

Теперь нетрудно убедиться, что

(3.8.34)

Это соотношение обеспечивает выполнение формулы (3.8.3). Затем имеем:

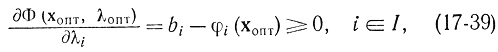(3.8.35)

так как множество I соответствует границе области. Эти разности неотрицательны, а остальные n - u равны нулю по условию. Формула (3.8.35) обеспечивает выполнение условия (17-23), которое по существу совпадает с ограничениями в исходной задаче нелинейного программирования. Наконец, условие (17-24) выполняется в силу доказанных ранее соотношений (17-17), согласно которым для ограничений в виде строгих неравенств

(3.8.36)

соответствующий множитель Лагранжа λ_i = 0 и λ_i ≠ 0 только при

(3.8.37)

Таким образом, доказано, что в точке оптимума задач нелинейного программирования выполняются необходимые и достаточные условия существования седловой точки (необходимость теоремы Куна - Таккера). Для доказательства достаточности этой теоремы необходимо дополнительно потребовать выпуклости (вогнутости) и использовать методы доказательства достаточности условий (3.8.2)-(3.8.7) для существования седловой точки. Тем самым доказана теорема Куна - Таккера для случая дифференцируемых функций.

В литературе имеются доказательства этой теоремы для не дифференцируемых функций F(х) и φ_i (х). В этом случае теорема формулируется следующим образом: вектор х_опт тогда и только тогда является решением задачи (3.8…..), когда существует вектор λ_опт, такой, что справедливы соотношения

x _опт≥0; λ_опт≥0; (17-40)

Φ (x_опт, λ) ≥ Φ (x_опт, λ_опт) ≥ Φ (х, λ_опт) (3.8.38)

для всех х ≥0 и λ≥0, т. е. задача о максимизации f (х) соответствует задаче о седловой точке, иными словами, задаче о максимине для функции L(х, λ).

ЛИТЕРАТУРА

[1] Алексеев В. М., Тихомиров В. М., Фомин С. В., Оптимальное управление, Наука, М., 1979 MathSciNet MathSciNet

[2] Сухарев А. Г., Тимохов А. В., Федоров В. В., Курс методов оптимизации, Наука, М., 1986 MathSciNet MathSciNet Zentralblatt MATH

[3] Васильев Ф. П., Методы оптимизации, В 2-х кн., МЦНМО, М., 2011

[4] Мину М., Математическое программирование. Теория и алгоритмы, Наука, М., 1990 MathSciNet MathSciNet

[5] Обен Ж.-П., Нелинейный анализ и его экономические приложения, Мир, М., 1988 MathSciNet MathSciNet

[6] Обен Ж.-П., Экланд И., Прикладной нелинейный анализ, Мир, М., 1988 MathSciNet MathSciNet

[7] Сумин М. И., “Регуляризованная параметрическая теорема Куна–Таккера в гиль- бертовом пространстве”, Ж. вычисл. матем. и матем. физ., 51:9 (2011), 1594– 1615 Math-Net.Ru MathSciNet MathSciNet Zentralblatt MATH

[8] Sumin M. I., “On the stable sequential Kuhn–Tucker theorem and its applications”, Appl. Math., 3:10A, Special issue “Optimization” (2012), 1334–1350

[9] Сумин М. И., “Оптимальное управление параболическими уравнениями: двой- ственные численные методы, регуляризация”, Распределенные системы: опти- мизация и приложения в экономике и науках об окружающей среде, Ин-т матем. и механ. УрО РАН, Екатеринбург, 2000, 66–69

[10] Сумин М. И., “Регуляризованный градиентный двойственный метод решения об- ратной задачи финального наблюдения для параболического уравнения”, Ж. вы- числ. матем. и матем. физ., 44:11 (2004), 2001–2019 Math-Net.Ru MathSciNet MathSciNet Zentralblatt MATH

[11] Сумин М. И., “Регуляризация в линейно выпуклой задаче математического про- граммирования на основе теории двойственности”, Ж. вычисл. матем. и матем. физ., 47:4 (2007), 602–625 Math-Net.Ru MathSciNet MathSciNet Zentralblatt MATH

[12] Sumin M. I., “Parametric dual regularization in a linear-convex mathematical programming”, Comput. Optimizat. New Res. Developments, Ch. 10, Nova Sci. Publ. Inc., New–York, 2010, 265–311

[13] Варга Дж., Оптимальное управление дифференциальными и функциональными уравнениями, Наука, М., 1977 MathSciNet MathSciNet

[14] Сумин М. И., “Регуляризованный двойственный метод решения нелинейной за- дачи математического программирования”, Ж. вычисл. матем. и матем. физ., 47:5 (2007), 796–816 Math-Net.Ru MathSciNet MathSciNet Zentralblatt MATH

[15] Sumin M. I., “Parametric dual regularization in a nonlinear mathematical programming”, Ch. 5, Advances Math. Res., 11, Nova Sci. Publ. Inc., New–York, 2010, 103–134

[16] Borwein J. M., Strojwas H. M., “Proximal analysis and boundaries of closed sets in banach space. Part I: Theory”, Can. J. Math., 38:2 (1986), 431–452 crossref MathSciNet MathSciNet Zentralblatt MATH; “Part II: Applications”, Can. J. Math., 39:2 (1987), 428–472 crossref Zentralblatt MATH

[17] Кларк Ф., Оптимизация и негладкий анализ, Наука, М., 1988 MathSciNet MathSciNet Zentralblatt MATH

[18] Loewen P. D., Optimal control via nonsmooth analysis, CRM Proc. Lecture Notes, 2, Amer. Math. Soc., Providence, RI, 1993 MathSciNet MathSciNet Zentralblatt MATH

[19] А. В. Канатов, М. И. Сумин Секвенциальная устойчивая теорема Куна–Таккера в нелинейном программировании Журнал вычислительной математики и математической физики, 2013, 53:8, 1249–1271.

ПРИЛОЖЕНИЕ

 

БЛОК 1.

Безусловные экстремумы (БУ)

1. ,

2. ,

3. ,

4. ,

5. ,

6. ,

7. ,

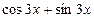8.

9.

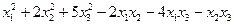
10. ,

11. ,

12. .

13.

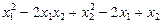
Условные экстремумы с ограничениями равенствами (УОР)

1) .

2) .

3) .

4. .

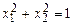5.

6.

7.

 

БЛОК 2.

Равенства, кроме №3.

Условные экстремумы с ограничениями неравенствами (УОН)

1.

2.

3.

БЛОК 4.

1) f (x) = − 2 x 2 − 3 x 2 + x 1 − 6 −→ max X,

X = {x | x 2 + x 1 − 3 ≤ 0, 2 x 1 + x 2 − 5 ≤ 0, x 2 ≥ 0 },

x 1 = (1, 1), x 2 = (2, 1), x 3 = (1 / 4, 0), x 4 = (0, 0);

2) f (x) = x 2 + 3 x 1 −→ min X,

X = {x | x 2 + x 2 − 2 x 1 + 8 x 2 + 16 ≤ 0, x 1 − x 2 ≤ 5 },

x 1 = (1, − 4), x 2 = (0, − 4), x 3 = (2, − 4);

3) f (x) = 7 x 2 + 2 x 2 − x 1 x 2 + x 1 − x 2 −→ min X,

X = {x | x 1 + x 2 ≤ 2, x 1 − 3 x 2 ≤ 4, − 2 x 1 + x 2 ≤ − 3 },

x 1 = (5 / 2, − 1 / 2), x 2 = (1, − 1), x 3 = (2, 0);

4) f (x) = x 2 / 2 + x 2 − 5 x 1 + x 2 −→ min X,

X = {x | x 1 + x 2 − 2 x 3 ≤ 3, 2 x 1 − x 2 − 3 x 3 ≥ − 11, x 1 ≥ 0, x 2 ≥ 0, x 3 ≥ 0 },

x 1 = (1, 0, 2), x 2 = (0, 0, − 1), x 3 = (1, 3, 0), x 4 = (2, 1, 1), x 5 = (5, 0, 1);

5) f (x) = ex 1+ x 2 + x 2 − 2 x 2 −→ min X, X = {x | x 2 ≤ ln x 1, x 1 ≥ 1, x 2 ≥ 0 }, x 1 = (2, ln 2), x 2 = (e, 0), x 3 = (1, 0);

6) f (x) = ex 1+ x 2 + x 2 + 2 x 1 + 2 x 2 −→ min X,

X = {x | x 2 + x 2 + x 2 ≤ 18, 2 x 1 + x 2 − x 3 + 3 ≤ 0 },

x 1 = (− 3, 3, 0), x 2 = (1, − 1, 4), x 3 = (− 3, − 3, 0), x 4 = (0, 0, 3);

7) f (x) = − 5 x 2 − 6 x 2 − x 2 + 8 x 1 x 2 + x 1 −→ max X,

X = {x | x 2 − x 2 + x 3 ≤ 5, x 1 + 5 x 2 ≤ 8, x 1 ≥ 0, x 2 ≥ 0 },

x 1 = (0, 0, 0), x 2 = (1, 0, 4), x 3 = (3 / 14, 1 / 7, 0), x 4 = (4, 0, − 11);

s) f (x) = −x 2 − 2 x 2 + x 1 x 2 − 26 −→ max X,

X = {x | x 2 ≤ 25, x 1 + 2 x 2 − 5 ≤ 0, x 2 ≥ 0 },

x 1 = (0, 0), x 2 = (− 1, 2), x 3 = (0, − 6), x 4 = (3, 0);

9) f (x) = 10 x 2 + 5 x 2 − x 1 + 2 x 2 − 10 −→ min X,

X = {x | 2 x 2 + x 2 ≤ 4, x 1 + x 2 ≤ 8, x 1 ≥ 0 },

x 1 = (0, 0), x 2 = (1, 1), x 3 = (0, − 1);

 

1n) f (x) = 4 x 2 + 3 x 2 + 4 x 1 x 2 − x 1 + 6 x 2 − 5 −→ min X,

X = {x | − x 2 − x 2 ≥ − 3, 3 x 2 + x 2 ≤ 4, x 1 ≥ 0, x 2 ≥ 0 },

x 1 = (0, 0), x 2 = (5, 0), x 3 = (1, − 1), x 4 = (1, 1);

 

11) f (x) = x 2 + 5 / 2 x 2 − x 1 x 2 −→ min X,

X = {x | x 2 − 4 x 1 − x 2 ≤ − 5, −x 2 + 6 x 1 − x 2 ≥ 7 },

x 1 = (2, 1), x 2 = (3, 2).

 

БЛОК 5. (№ 13-15 – без ограничений, №1-12 – неравенства)

1) f (x) = x 1 x 2 − x 2 − 2 x 2 + x 1,

X = {x | x 1 ∈ [0, 1], x 2 ∈ [0, 1] };

2) f (x) = x 3 − 4 x 2 + 2 x 1 x 2 − x 2,

X = {x | |x 1 | ≤ 5, |x 2 | ≤ 1 };

3) f (x) = x 3 + x 3 − 3 x 1 x 2,

X = {x | x 1 ∈ [0, 2], x 2 ∈ [ − 1, 2] };

4) f (x) = (x 1 − 5)2 + (x 2 − 7)2,

X = {x | x 1 + 2 x 2 ≤ 12, x 1 + x 2 ≤ 9, x 1 ≥ 0, x 2 ≥ 0 };

5) f (x) = (x 1 − 3)2 + (x 2 − 5)2,

X = {x | x 2 + x 2 ≤ 10, 2 x 1 + 2 x 2 = 5 };

6) f (x) = x 1(π − x 1) sin x 2 + x 2 cos x 1, X = {x | x 1 ∈ [0, π ], x 2 ≥ 0 };

7) f (x) = x 1 + x 2 + x 3,

X = {x | x 2 + x 2 ≤ x 3, x 3 ≤ 1 };

s) f (x) = 2 x 1 x 2 + x 3,

X = {x | x 2 + x 2 = 1, 0 ≤ x 3 ≤ 2 x 1 + 1 };

9) f (x) = x 2 − x 2,

X = {x | x 2 + x 2 ≤ 16 };

10) f (x) = x 2 + x 2 − 12 x 1 + 16 x 2,

X = {x | x 2 + x 2 ≤ 25 };

11) f (x) = arctg x 1 − ln x 2,

X = {x | x 2 + x 2 ≤ 4, x 1 ≥ 0, x 2 ≥ 1 };

12) f (x) = x 1 + x 2 − x 3,

X = {x | x 1 x 2 x 3 ≤ 1, −x 1 + x 2 − x 3 ≤ 0 };

13) f (x) = x 2 + x 1 x 2 + x 2 + 3 |x 1 + x 2 + 2 |,

X = R² = E 2;

 

 

14) f (x) = x 2 + x 2 + 2 α|x 1 + x 2 − 1 |, α > 0,

X = R² = E 2;

15) f (x) = x 2 + x 2 + 2 max {x 1, x 2 },

X = R² = E 2.

 

БЛОК 6.

Ограничения равенства.

Ограничения неравенства.

 

ТЕЗИСЫ ЛЕКЦИЙ И ЛАБОРОТОРНЫХ ЗАНЯТИЙ

(на основе книги Пантелеева)

1 ИСТОРИЯ РАЗВИТИЯ МЕТОДОВ ОПТИМИЗАЦИИ И ОБЗОР КУРСА.. 3

1.1 Основные этапы развития теории оптимизации. 3

1.2 Обзор курса. 7

2 АЛГОРИТМЫ МЕТОДОВ ПОИСКА ЭКСТРЕМУМОВ.. 10

2.1 Классификация методов программирования. 10

2.2 Необходимые и достаточные условия безусловного экстремума (§ 20) 10

3 ТЕОРЕМА КУНА-ТАККЕРА.. 39

3.1. Предыстория: линейное программирование и принцип и метод Лагранжа. 39

3.2. Классификация задач нелинейного программирования. 41

3.3. Метод Лагранжа. 48

3.4. Банаховы и гильбертовы пространства. 51

3.5. Роль выпуклости. 52

3.6. Формулировка и доказательство теоремы Куна-Таккера. 53

Если непрерывная функция n переменных x = (x1,...,xn) F(х) имеет в точке х _опт максимум, то существует ε > 0 такое, что для всех x из ε-окрестности точки х _опт 55

3.7. Минимаксная трактовка задачи на условный экстремум.. 58

3.8. Минимаксная трактовка задачи на условный экстремум.. 63

3.9. Теорема Куна-Таккера. 69

3.10. Связь теоремы Куна-Таккера с теорией игр и седловыми точками. 72

ЛИТЕРАТУРА.. 74

ПРИЛОЖЕНИЕ.. 75