Туннельный эффект играет важную роль в квантовой физике. Он проявляется в автоэлектронной эмиссии, контактных явлениях в полупроводниках (в туннельных диодах) и наноструктурах, при альфа-распаде, делении и слиянии атомных ядер.
Компьютерная модель туннельного эффекта (см. Прил. 8) реализуется при запуске исполняемого файла tunnel . exe в папке “Туннельный диод” на рабочем столе компьютера с операционной системой Windows. В программе используется так называемые атомная система единиц, в которой постоянная Планка 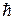 =1, масса электрона
=1, масса электрона 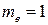 , единицей длины служит Боровский радиус
, единицей длины служит Боровский радиус 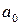 , равный 0.0529 нм, единицей энергии служит величина, равная 27.21 эВ (удвоенному значению энергии состояния 1s атома водорода). Данные для расчета вносятся в текстовый файл input . txt:
, равный 0.0529 нм, единицей энергии служит величина, равная 27.21 эВ (удвоенному значению энергии состояния 1s атома водорода). Данные для расчета вносятся в текстовый файл input . txt:
3 3. 1 0.5 2.4 0.1
2 3. 1. 2 2 1
1 3. 1. 2 2 1
Npot U0 a E1 E2 DE
В каждой строке: первый параметр Npot – номер потенциального барьера: 1 – прямоугольный потенциальный барьер (см. рис. 16.13б), 2 – барьер в форме колокола, 3 – два прямоугольных барьера, между которыми образуется прямоугольная потенциальная яма конечной глубины (см. рис. 17.12). Второй параметр U0 – высота потенциального барьера. Третий параметр – ширина барьера. Затем идут начальное E1 и конечное E2 значения энергии налетающего на потенциальный барьер электрона и приращение энергии DE. Результаты расчета проницаемости барьера D в виде двух колонок E и D записываются в текстовый файл result . txt. Графики квадрата модуля волновой функции 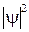 и потенциального барьера и зависимости D(E) выводятся на экран (см. рис. 17.11).
и потенциального барьера и зависимости D(E) выводятся на экран (см. рис. 17.11).
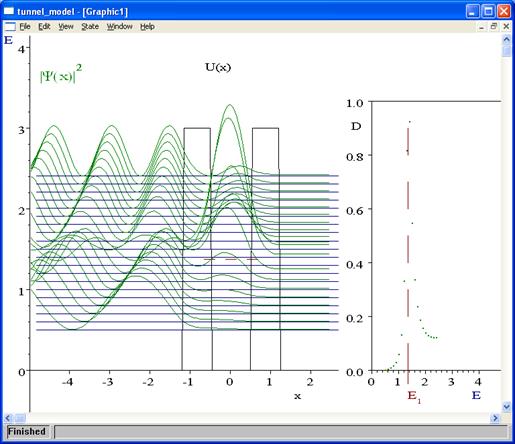
а б
Рис. 17.11. Потенциальный барьер с потенциальной ямой, имеющей уровень энергии 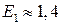 , квадрат модуля волновой функции (а) и зависимость проницаемости D барьера от энергии E (б)
, квадрат модуля волновой функции (а) и зависимость проницаемости D барьера от энергии E (б)
Запустите компьютерную модель туннельного эффекта и выполните следующие задания по указанию преподавателя.
1. Изучение туннельного эффекта на потенциальном барьере в форме колокола. Получите на экране изображение квадрата модуля волновой функции для энергии электрона много меньше высоты барьера, чуть меньшей и чуть большей высоты барьера. Зарисуйте схематично изображение с экрана в тетрадь. Получите таблицу зависимости проницаемости барьера от энергии при энергиях от 0.1 до 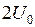 . Постройте вручную или на компьютере с помощью программы Origin зависимости D(E).
. Постройте вручную или на компьютере с помощью программы Origin зависимости D(E).
2. Изучение туннельного эффекта на потенциальном барьере с потенциальной ямой, имеющей уровень энергии  (рис. 17.12). Получите на экране изображение квадрата модуля волновой функции для энергии электрона много меньше уровня
(рис. 17.12). Получите на экране изображение квадрата модуля волновой функции для энергии электрона много меньше уровня  , чуть меньшей, равной и чуть большей
, чуть меньшей, равной и чуть большей  . Зарисуйте схематично изображение с экрана в тетрадь. Получите таблицу зависимости проницаемости барьера от энергии при энергиях от 0,1 до
. Зарисуйте схематично изображение с экрана в тетрадь. Получите таблицу зависимости проницаемости барьера от энергии при энергиях от 0,1 до 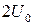 , она сохраняется в файле result.txt. Постройте вручную или на компьютере с помощью программы Origin зависимости D(E). В программе Origin выполните команду File-Import-ASCII, в диалоговом окне укажите путь к файлу, щелкните ОК. Найдите на графике характерные участки возрастания и убывания D(E) вблизи
, она сохраняется в файле result.txt. Постройте вручную или на компьютере с помощью программы Origin зависимости D(E). В программе Origin выполните команду File-Import-ASCII, в диалоговом окне укажите путь к файлу, щелкните ОК. Найдите на графике характерные участки возрастания и убывания D(E) вблизи 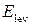 , а также возрастания D(E) при
, а также возрастания D(E) при 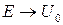 . Пример показан на рис. 17.12. Сопоставьте этим участкам участки ВАХ туннельного диода.
. Пример показан на рис. 17.12. Сопоставьте этим участкам участки ВАХ туннельного диода.
Контрольные вопросы
1. Расскажите об образовании p - n -перехода.
2. Как действует внешнее напряжение на p - n -переход в сильно легированных полупроводниках.
3. Расскажите о туннельном эффекте, свойствах волновой функции и проницаемости потенциального барьера.
4. Объясните свойства ВАХ туннельного диода и сравните ее с результатами компьютерного моделирования.
5. Для чего применяются туннельные и обращенные диоды в электронных устройствах.
ПРИЛОЖЕНИЯ
Приложение 1.
Типовые лабораторные установки по квантовой физике серий ФПК*1 и ФКЛ*2
1. Установка для изучения излучения абсолютно черного тела ФПК 11м (см. рис. П1.1) состоит из электропечи и измерительного устройства с термостолбиком. Она позволяет изучать законы излучения абсолютно черного тела и исследовать его испускательную способность, а также убедиться в правильности закона Стефана-Больцмана. Обеспечивается возможность работы ПЭВМ типа IBM РС через интерфейс RS-232.

Рис. П1.1. Установка для изучения излучения абсолютно черного тела ФПК 11м
Технические характеристики установки: максимальная температура электропечи 800°С, электропитание от сети переменного тока напряжением 220 В, частотой 50 Гц, потребляемая мощность 500 В·А, габаритные размеры, мм: электропечи 150х180х380, устройства измерительного 340х75х310, термостолбика 190х190х150, общая масса 14 кг.
2. Установка для изучения внешнего фотоэффекта и измерения постоянной Планка ФПК-10* (см. рис. П1.2) состоит из осветителя (спектральной ртутной лампы) с источником питания, блока интерференционных светофильтров (1,2,3,4), устройства регулировки освещенности (диафрагмы), усилителя фототока, фотоприемников с фотоэлементами Ф-8 и Ф-25 и измерительного устройства. Она позволяет определять значение постоянной Планка и экспериментально проверить уравнение Эйнштейна для фотоэффекта.

Рис. П1.2. Установка для изучения внешнего фотоэффекта и измерения постоянной Планка ФПК-10м
Технические характеристики установки: диапазоны измерения фототока, мкА: от 0 до 0,1999, от 0 до 1,999, от 0 до 19,99, от 0 до 199,9; диапазон регулируемых анодных напряжений фотоэлемента, мкА: при прямом режиме измерения от 0 до 10, при обратном режиме измерения от 0 до –1; количество устанавливаемых диафрагм – 4, интерференционных светофильтров– 5. Электропитание от сети переменного тока напряжением 220 В частотой 50 Гц, потребляемая мощность 200 В·А, габаритные размеры, мм: блока измерительного 500х350х200, объекта исследования 420х200х200, общая масса 23 кг.
Более совершенная аналогичная установка ФКЛ-11 (см. http://physexperiment.narod.ru/physics.htm) состоит из объекта исследования (фотоэлемента СЦВ-3), устройства измерительного (блока управления) и монохроматора МУМ-1.
3. Установка для изучения спектра атома водорода ФПК 09м *1 (см. рис. П1.3) состоит из излучателя (водородной газоразрядной трубки, см. Прил. 2) и монохроматора МУМ. Она позволяет исследовать спектр испускания нагретого газа водорода; определять постоянную Ридберга; наблюдать линейчатый спектр атома водорода (часть серии Бальмера) и измерять длины волн спектральных линий с помощью спектрального аппарата (монохроматора типа МУМ).

Рис. П1.3. Установка для изучения внешнего фотоэффекта и измерения постоянной Планка ФПК-10м
Электропитание от сети переменного тока напряжением 220 В частотой 50 Гц, потребляемая мощность 500 В·А, габаритные размеры, мм: блока измерительного 500х350х200, объекта исследования 420х200х200, общая масса 60 кг.
Более совершенная аналогичная установка ФКЛ-1 (см. http://physexperiment.narod.ru/physics.htm) включает излучатель с водородной лампой ДВС-25 (дуговой водородной спектральной мощностью 25 Вт) и ртутной лампой ДРСк-125.
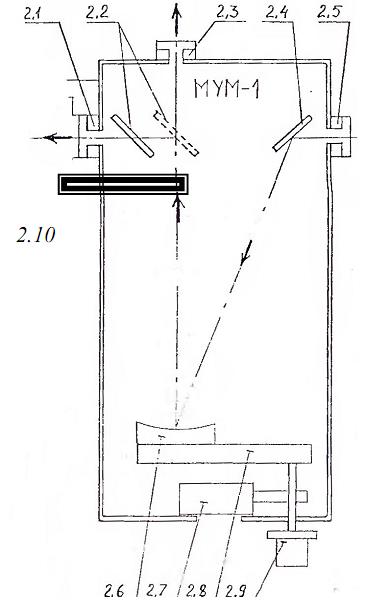
Монохроматор МУМ-1 (см. рис. П1.4) имеет сферическую дифракционную решетку 2.6, боковой выход 2.3, задний выход 2.1, механизм 2.8 поворота решетки и связанный с ним механизм 2.7 отсчета длины волны излучения с приводом от вала с ручкой 2.9. на входе и на выходах имеется возможность устанавливать сменные щели. Излучение, вошедшее во входную щель 2.5, направляется на дифракционную решетку 2.6 неподвижным зеркалом 2.4. Длина волны излучения, отраженного от решетки в направлении выхода монохроматора зависит от ориентации решетки. Поворот решетки осуществляется вращением ручки 2.9. Длина волны отсчитывается по шкале 2.7 отсчетного устройства.
| Рис. П1.4. Монохроматор учебный
малогабаритный МУМ-1. Вид сверху.
| 
|
4. Установка для определения резонансного потенциала методом Франка и Герца ФПК 02м*1 (см. рис. П1.5) состоит из объекта исследования (газонаполненной электронной лампы), устройства измерительного и осциллографа. Она позволяет воспроизводить классический опыт Франка и Герца по определению резонансного потенциала и измерять энергию резонансного уровня. Для исследования зависимости анодного тока лампового газонаполненного триода от напряжения сетка-катод (вольт-амперную характеристику) с максимумами и минимумами, характерными для опыта Франка и Герца, используется осциллограф любого типа. Обеспечивается возможность работы ПЭВМ типа IBM РС через интерфейс CENTRONIX.

Рис. П1.5. Установка для определения резонансного потенциала методом Франка и Герца ФПК 02м
Электропитание от сети переменного тока напряжением 220 В частотой 50 Гц, потребляемая мощность 60 В·А, габаритные размеры, мм: устройства измерительного 240х75х310, объекта исследования 350х190х190, общая масса 12 кг. Режимы снятия вольт-амперной характеристики газонаполненной лампы: ручной и автоматический, пределы регулировки напряжения Ukg газонаполненной лампы в ручном режиме, В 0...50; пределы регулировки амплитудного значения напряжения пилообразного импульса Ukg газонаполненной лампы в автоматическом режиме, В 0...50; пределы регулировки напряжения Uag газонаполненной лампы, B 0...5, пределы регулировки напряжения накала газонаполненной лампы, В 3...8. Замер значений напряжения катод-сетка в экстремальных точках вольтамперной характеристики лампы Ia=F(Uac): цифровой погрешность измерения напряжения катод-сетка (мгновенное значение) не более 4% от максимальной величины соответствующего предела измерения; пределы измерения напряжения катод-сетка газонаполненной лампы, В 0,0...99,9.
Более совершенная аналогичная установка ФКЛ-6 (см. http://physexperiment.narod.ru/physics.htm) включает исследуемый триод
ПМИ-2 либо ТГ1-0.1/0.3 в которую введено строго дозированное количество инертного газа (паров ртути).
5. Установка для изучения р-n перехода ФПК 06м* (см. рис. П1.6) состоит из измерительного устройства, к гнезду которого присоединяется блок с диодами. Она позволяет исследовать прямую и обратную вольт-амперные характеристики (ВАХ) и вольт-фарадную характеристику(ВФХ) p-n перехода. Обеспечивается возможность работы ПЭВМ типа IBM РС через интерфейс RS-232.

Рис. П1.6. Установка для изучения р-n перехода ФПК 06м
Технические характеристики установки: диапазон измерения напряжения, В: при исследовании ВАХ прямой от 0 до 5; при исследовании ВАХ обратной и ВФХ от 0 до 30. Диапазон измерения тока: при исследовании ВАХ прямой, мА от 0 до 50 при исследовании ВАХ обратной, мкА от 0 до 99,9. Диапазон измерения емкости при исследовании ВФХ, пф от 0 до 999. Электропитание от сети переменного тока напряжением 220 В частотой 50 Гц, потребляемая мощность 60 В·А, габаритные размеры, мм: устройства измерительного 250х80х330, объекта исследования 50х30х100, общая масса 4 кг.
Более совершенная аналогичная установка ФКЛ-18У включает электронный осциллограф (см. http://physexperiment.narod.ru/physics.htm) и демонстрирует на экране осциллографа в режиме реального времени вольтамперную характеристику p-n-перехода, как в прямом, так и в обратном направлении. При помощи вольтамперной характеристики оцениваются основные параметры перехода: потенциальный барьер, ширина запирающего слоя перехода, а также численно оценивается значение константы Больцмана.
Приложение 2.
Физические процессы при электрическом разряде
в гейслеровской водородной трубке
Спектр атомарного водорода получают с помощью газоразрядной гейсслеровской трубки*, наполненной молекулярным водородом Н2 под давлением 0,7 – 1,3 кПа (5-10 мм. рт. ст.). Электрический разряд происходит между медными электродами, впаянными по концам трубки. Наибольшая интенсивность излучения происходит в средней - капиллярной, части трубки. После возникновения разряда медные электроды разогреваются, и имеющаяся на них окись меди CuO отдает атомарный кислород О. Атомы кислорода длительное время существуют в трубке, поскольку рекомбинация двух атомов кислорода с образованием молекулы О2 при парном столкновении О+О невозможна из-за нарушения законов энергии и импульса (легче всего в этом можно убедиться, рассматривая столкновение в системе центра масс). Для ее осуществления необходимо участие в столкновении третьего объекта Х (атома, молекулы или стенки трубки):
О+О+Х 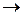 О2+Х, (П2.1)
О2+Х, (П2.1)
а такие тройные столкновения сравнительно редки. Атомы кислорода в основном состоянии (3Р) могут вступать в эндотермическую реакцию (идущую с поглощением энергии Q = 0.07 эВ) с молекулой водорода
О(3Р)+Н2+0.07 эВ 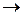 ОН+Н, (П2.2)
ОН+Н, (П2.2)
только, если их кинетическая энергия поступательного движения 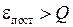 . Для этого температура газа Т должна быть достаточно высокой, Т > 550 К, чтобы средняя кинетическая энергия атомов превышала порог реакции
. Для этого температура газа Т должна быть достаточно высокой, Т > 550 К, чтобы средняя кинетическая энергия атомов превышала порог реакции
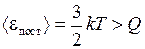 , (П2.3)
, (П2.3)
где k - постоянная Больцмана.
Атомы кислорода при столкновениях c электронами могут переходить в возбужденное состояние 1D, обратный переход из которого в основное состояние 3Р с испусканием фотона запрещен правилом отбора 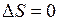 , где S - спин атома. Поэтому такое состояние является долгоживущим (метастабильным). Атом кислорода, находящийся длительное время в возбужденном состоянии 1D, может столкнуться с молекулой водорода и вызвать протекание экзотермической реакции (идущей с выделением энергии
, где S - спин атома. Поэтому такое состояние является долгоживущим (метастабильным). Атом кислорода, находящийся длительное время в возбужденном состоянии 1D, может столкнуться с молекулой водорода и вызвать протекание экзотермической реакции (идущей с выделением энергии 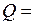 1.97 эВ)
1.97 эВ)
О(1D)+Н2 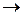 ОН+Н+1.97 эВ. (П2.4)
ОН+Н+1.97 эВ. (П2.4)
В ходе этой реакции образуется атомарный водород и химически нестабильная молекула гидроксила ОН. Эта реакция в свою очередь приводит к ряду разветвляющихся химических реакций с участием гидроксила, в ходе которых из молекулярного водорода также образуется атомарный водород. В следующем примере в трех последовательных реакциях из двух молекул Н2 образуется три атома Н
Н2+ОН 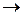 Н2О+Н, (П2.5)
Н2О+Н, (П2.5)
Н2О + 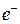
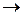 ОН +Н+
ОН +Н+ 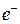 , (П2.6)
, (П2.6)
Н2+ОН 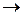 Н2О+Н. (П2.7)
Н2О+Н. (П2.7)
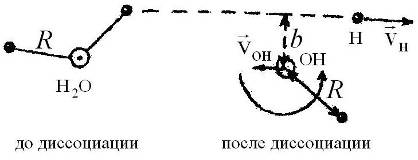
Процесс диссоциации молекулы воды (П2.6) схематически показан на рис. П2.1. Его особенностью является сильное закручивание образующейся двухатомной молекулы ОН. Для объяснения этого явления применим к процессу диссоциации законы сохранения импульса и момента импульса и найдем кинетическую энергию 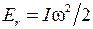 вращения с угловой скоростью w молекулы ОН с моментом инерции I. Пусть молекула воды до столкновения покоилась, тогда из закона сохранения импульса следует,
вращения с угловой скоростью w молекулы ОН с моментом инерции I. Пусть молекула воды до столкновения покоилась, тогда из закона сохранения импульса следует,
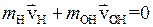 ,
, 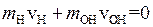 . (П2.8)
. (П2.8)
| Рис. П2.1. Схема диссоциации молекулы воды
| 
|
Для диссоциации молекулы воды, показанной на рис. П1.1 модуль момента импульса атома Н относительно центра масс молекул Н2О, ОН, приближенно совпадающим с ядром атома О, равен 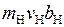 . Вследствие закона сохранения момента импульса модуль момента импульса молекулы ОН с моментом инерции I равен
. Вследствие закона сохранения момента импульса модуль момента импульса молекулы ОН с моментом инерции I равен
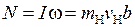 . (П2.9)
. (П2.9)
Используя формулы (П2.9) и (П2.8) выразим скорости продуктов диссоциации через угловую скорость w
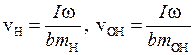 . (П2.10)
. (П2.10)
Кинетическая энергия DE образовавшейся системы Н+ОН складывается из кинетической энергии поступательного движения продуктов и кинетической энергии вращения молекулы ОН
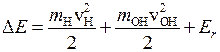 . (П2.11)
. (П2.11)
В результате преобразований с учетом большой разницы в массах 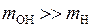 и выражения для момента инерции
и выражения для момента инерции 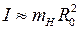 , получим
, получим
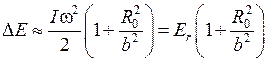 . (П2.12)
. (П2.12)
В приближении 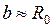 можно увидеть, что во вращательную энергию переходит примерно половина всего приращения кинетической энергии системы.
можно увидеть, что во вращательную энергию переходит примерно половина всего приращения кинетической энергии системы.
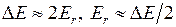 . (П2.13)
. (П2.13)
Именно это объясняет сильное закручивание образующейся двухатомной молекулы ОН и образование интенсивных протяженных вращательных полос ОН в спектре излучения гейсслеровской трубки.
Приложение 3.
Универсальный монохроматор УМ-2 и его градуировка
Для разложения исследуемого излучения в спектр используется универсальный монохроматор УМ-2. Внешний вид монохроматора показан на рис. П3.1.
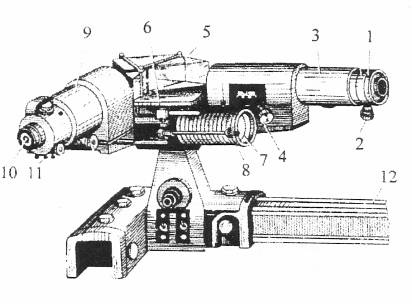
| Рис. П3.1. Универсальный монохроматор УМ-2: 1 − входная щель, 2 − микрометрический винт щели, 3 − коллиматорный объектив, 4 − микрометрический винт объектива, 5 − призма Аббе, 6 − поворотный столик, 7 − барабан для поворота столика, 8 − указатель поворота барабана, 9 − объектив и 10 − окуляр зрительной трубы, , 11 − указатель.
|
Принципиальная схема монохроматора УМ-2 показана на рис. П3.2. Свет от лампы падает на входную щель коллиматора, находящуюся в фокусе объектива коллиматора. Световой пучок, выходящий из коллиматора, преломляется призмой Аббе, которая может поворачиваться с помощью барабана. Призма Аббе состоит из двух 30-градусных призм и одной 45-градусной, служащей для поворота луча на 90º .Большие катеты 30-градусных призм приклеены к катетам 45-градусной призмы. Призма Аббе имеет следующее свойство: интенсивность преломленного луча максимальна, когда он перпендикулярен падающему лучу. Поэтому выходная труба монохроматора установлена перпендикулярно падающему пучку света. В ней преломленный световой пучок фокусируется камерным ахроматическим объективом. При визуальных наблюдениях в фокусе объектива устанавливают указатель (острие), который может подсвечивать дополнительной лампой через набор светофильтров. Указатель и получаемое в фокусе монохроматическое изображение щели рассматривается (см. рис. П.3.3) с помощью окуляра, дающего 10-кратное увеличение. Вместо указателя с окуляром в фокусе объектива может устанавливаться выходная щель. Поворачивая с помощью барабана 5 призму 4, получают у острия указателя 8 или в выходной щели свет с различной длиной волны 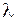 . Зависимость
. Зависимость 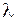 от угла поворота барабана
от угла поворота барабана 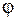 называется градуировочной кривой (градуировочным графиком), с ее помощью определяют длины волн
называется градуировочной кривой (градуировочным графиком), с ее помощью определяют длины волн 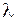 .
.
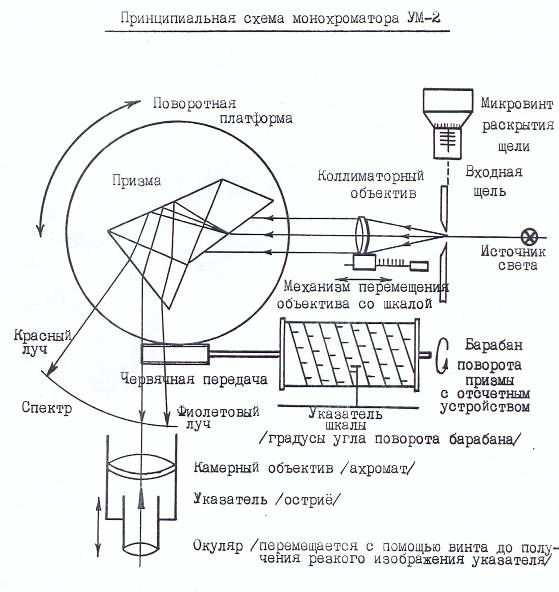
П3.2. Принципиальная схема монохроматора УМ-2
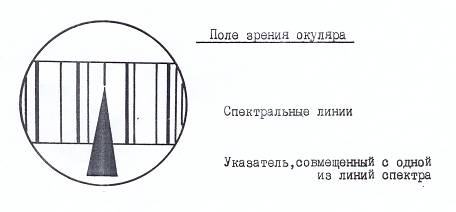
П3.3. Наблюдение спектральных линий с помощью монохроматора УМ-2
Для построения градуировочного графика l = l(j) требуется измерение углов отклонения j для набора эталонных (например, ртутных и неоновых) спектральных линий с известными значениями длин волн l (см. табл. П3.1).
Таблица П3.1.
| Лампа
| № линии
| Цвет линии
| Относительная интенсивность
| l, нм
| Угол j
|
| Неоновая
| 1
| темно красный
| 1
| 703.2
|
|
| 2
| темно красный
| 1
| 692.9
|
|
| 3
| темно красный
| 1
| 671.7
|
|
| 4
| темно красный
| 3
| 667.8
|
|
| 5
| темно красный
| 5
| 659.9
|
|
| 6
| красный
| 5
| 653.3
|
|
| 7
| красный
| 5
| 650.6
|
|
| 8
| красный
| 10
| 640.2
|
|
| 9
| красный
| 10
| 638.3
|
|
| 10
| красный,
| 5
| 633.4
|
|
| 11
| красный
| 2
| 630.5
|
|
| 12
| красный
| 8
| 626.7
|
|
| 13
| красный
| 3
| 621.7
|
|
| 14
| красный
| 5
| 616.4
|
|
| 15
| красный
| 5
| 614.3
|
|
| 16
| оранжевый
| 3
| 609.6
|
|
| 17
| оранжевый
| 4
| 607.4
|
|
| 18
| оранжевый
| 5
| 603.0
|
|
| 19
| оранжево-желтый
| 3
| 597.66
|
|
| 20
| оранжево-желтый
| 3
| 594.5
|
|
| 21
| желтый
| 4
| 588.2
|
|
| 22
| желтый
| 10
| 585.2
|
|
| 23
| зеленый
| 2
| 540.0
|
|
| Ртутная
| 1
| желтый
| 10
| 579.06
|
|
| 2
| желтый
| 8
| 576.96
|
|
| 3
| зеленый
| 10
| 546.06
|
|
| 4
| голубой
| 1
| 491.60
|
|
| 5
| сине-фиолетовый
| 10
| 435.83
|
|
| 6
| фиолетовый
| 1
| 407.78
|
|
| 7
| фиолетовый
| 2
| 404.68
|
|
Производная 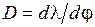 называется угловой дисперсией монохроматора. В красно-оранжевой области спектра величина дисперсии велика, поэтому для градуировки необходимо использовать больше линий (из спектра неона), чем в остальных участках спектра. Изображение фотопластинки со спектром неоновой лампы и схема расположения спектральных линий показаны на рис. П3.4.
называется угловой дисперсией монохроматора. В красно-оранжевой области спектра величина дисперсии велика, поэтому для градуировки необходимо использовать больше линий (из спектра неона), чем в остальных участках спектра. Изображение фотопластинки со спектром неоновой лампы и схема расположения спектральных линий показаны на рис. П3.4.


Рис. П3.4. Изображение фрагмента фотопластинки со спектром излучения неоновой лампы (вверху) и схема расположения спектральных линий (внизу). Расположение линий соответствует видимому в окуляр универсального монохроматора УМ-2. Длины волн приведены в ангстремах, Å, 10 Å=1 нм. Толщина линии пропорциональна ее интенсивности.
Выполните градуировку призменного спектрографа в следующем порядке.
1. Микровинтом раскрытия щели монохроматора задайте ширину щели 0.01 мм. Установите рейтер с неоновой лампой вплотную к приемному окну монохроматора. Включите неоновую лампу в электрическую сеть напряжением ~220 В.
2. Рассмотрите спектр излучения в красно-желтой области. Самая характерная линия в спектре неона – интенсивная желтая линия. Слева от нее расположены многочисленные оранжевые и красные линии. Наблюдение спектральных линий начните с красной области. Сначала найдите характерную группу из 5 линий (одна в центре и по две близких линии на одинаковом удалении слева и справа от нее). Вращая барабан монохроматора, совмещайте перечисленные в табл. П3.1 и на рис. П3.4 линии с указателем монохроматора и записывайте в табл. П3.1 цвет линии, угол поворота барабана 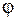 , примерную интенсивность линии по 10-бальной шкале (за 10 принять интенсивность желтой линии). Закончив измерение зеленой линии, выключите неоновую лампу.
, примерную интенсивность линии по 10-бальной шкале (за 10 принять интенсивность желтой линии). Закончив измерение зеленой линии, выключите неоновую лампу.
3. Установите рейтер с ртутной лампой на расстоянии 20-25 см от приемного окна монохроматора. Включите ртутную лампу в электрическую сеть напряжением ~220 В.
4. Спектр ртутной лампы мощностью 11 Вт фирмы R & C содержит линии, приведенные в табл. П3.1 на фоне относительно слабого и монотонного сплошного спектра свечения люминофора. Наблюдение спектральных линий начните с желтой области. Вращая барабан монохроматора, совмещайте линии с указателем монохроматора и записывайте в табл. П3.1 цвет линии, угол поворота барабана 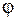 , примерную интенсивность линии по 10-бальной шкале (за 10 принять интенсивность зеленой линии). При переходе от желтой области к фиолетовой следует подстраивать резкость линий с помощью микровинта, перемещающего коллиматорный объектив. Резкость указателя в поле зрения окуляра регулируется кольцом окуляра. При необходимости подсвечивайте указатель. В фиолетовой части спектра видимость линий ухудшается. Для улучшения видимости линий увеличивайте ширину щели и совмещайте с указателем центр уширенной из-за отсутствия резкости линии. Пройдите весь спектр до его фиолетовой части, результаты внесите в табл. 6.3. Выключите ртутную лампу.
, примерную интенсивность линии по 10-бальной шкале (за 10 принять интенсивность зеленой линии). При переходе от желтой области к фиолетовой следует подстраивать резкость линий с помощью микровинта, перемещающего коллиматорный объектив. Резкость указателя в поле зрения окуляра регулируется кольцом окуляра. При необходимости подсвечивайте указатель. В фиолетовой части спектра видимость линий ухудшается. Для улучшения видимости линий увеличивайте ширину щели и совмещайте с указателем центр уширенной из-за отсутствия резкости линии. Пройдите весь спектр до его фиолетовой части, результаты внесите в табл. 6.3. Выключите ртутную лампу.
3. По данным табл. П3.1 постройте примерный градуировочный график l = l(j) (см. Прил.4). Если кривая получится не очень гладкой, с изломами, повторно измерьте 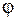 и проверьте, правильно ли сопоставлены линиям длины волн. Добейтесь получения гладкой кривой (см. рис. П4.1 в Прил.4).
и проверьте, правильно ли сопоставлены линиям длины волн. Добейтесь получения гладкой кривой (см. рис. П4.1 в Прил.4).
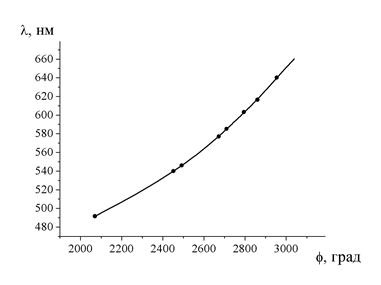
5. С помощью программы (исполняемого файла) splines.exe, выполняющей сглаживание градуировочных данных сплайнами (см. Прил. 5) подберите значение параметра 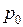 , при котором градуировочный график l = l(j) будет достаточно гладкой линией, см. рис. П3.5. При этом необязательно использовать все линии неона из табл. П3.1.
, при котором градуировочный график l = l(j) будет достаточно гладкой линией, см. рис. П3.5. При этом необязательно использовать все линии неона из табл. П3.1.
| Рис. П3.5. Градуировочный график монохроматора УМ-2, построенный путем сглаживания сплайнами (см. Прил. 5)
| 
|
Приложение 4.
Программы научной графики Origin и
Advanced Grapher
1. Программу научной графики MicroCal Origin (не требующую лицензии версию 3.0) удобно использовать для быстрого построения градуировочных графиков призменных спектральных приборов (необходимых при выполнении работ 5, 6, 9-13), пример показан на рис. П4.1.
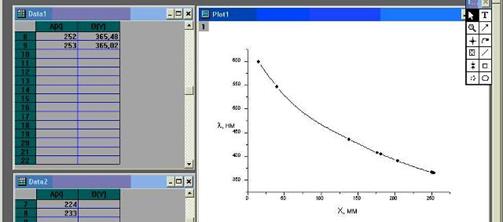
Рис. П4.1. Пример построения градуировочного графика
с помощью программы MicroCal Origin 3.0
Для построения подобного показанному на рис. П4.1 графика выполните следующие действия. Запустите программу и внесите данные на рабочую область Data1, при этом нажимайте клавишу Enter после ввода каждого числа. Затем выделите оба столбца и выполните команду Plot - Scatter (Рисовать-Разброс). Для соединения точек плавной линией (интерполяции) щелкните левой кнопкой мыши по одной из точек и в диалоговом окне Plot Details в поле Line - Connect (Линия-Соединение) выберите Spline (Сплайн).
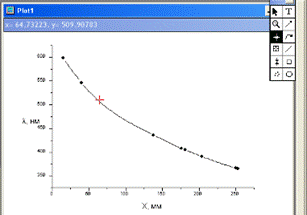
Определение по градуировочному графику (например, по графику l = l(x)) значений длин волн выполняется с помощью инструмента Перекрестие (рис. П4.2).
| Рис. П4.2. Оценка длины волны спектральной линии с помощью градуировочного графика в программе MicroCal Origin 3.0.
| 
|
2. Выполнение расчетов с многократным применением одной формулы рассмотрим на примере нахождения значений обратной длины волны – спектроскопического волнового числа 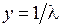 . Для этого в рабочей области выделите столбец, содержащий значения длин волн, выполните команду Edit - Insert (Редактировать-Вставить). Выделите новый столбец, выполните команду Data - Set Column Values … (Данные-Установить значения для колонки). В диалоговом окне введите формулу для вычисления обратных значений (рис. П4.3), щелкните по кнопке Do it (Сделать это).
. Для этого в рабочей области выделите столбец, содержащий значения длин волн, выполните команду Edit - Insert (Редактировать-Вставить). Выделите новый столбец, выполните команду Data - Set Column Values … (Данные-Установить значения для колонки). В диалоговом окне введите формулу для вычисления обратных значений (рис. П4.3), щелкните по кнопке Do it (Сделать это).
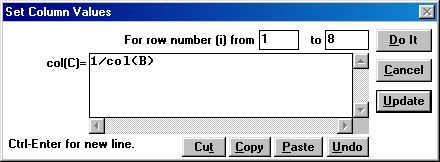
Рис. П4.3. Ввод формулы для вычислений в программе MicroCal Origin 3.0
Программа Advanced Grapher* (Улучшенный Графопостроитель) предназначена для построения и анализа графиков по табличным данным и формулам. Типичный вид рабочего окна программы показан на рис. П.4.4. Для вычислений используется панель Калькулятор (на рис. П.4.4 слева), центральное окно служит для построения графиков функций.
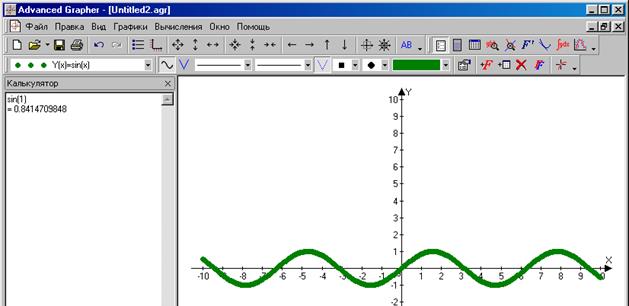
Рис. П.4.4. Окно программы Advanced Grapher с графиком функции 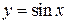
Для ввода функции, график которой нужно построить, щелкните по кнопке + F (Добавить график), затем в диалоговом окне (см. рис. П.4.5) введите функцию. Для редактирования выражения щелкните по кнопке  (см. рис. П.4.5) и в диалоговом окне (рис. П.4.6) сделайте необходимые изменения.
(см. рис. П.4.5) и в диалоговом окне (рис. П.4.6) сделайте необходимые изменения.
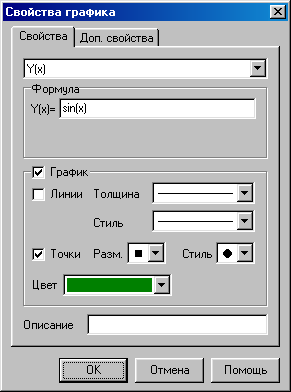
| Рис. П.4.5. Диалоговое окно для ввода и изменения вида функции на графике в программе Advanced Grapher
| 
|
Для изменения интервалов щелкните по кнопке Свойства документа  (см. рис. П.4.5) и введите в поля (рис. П.4.6) нужные значения.
(см. рис. П.4.5) и введите в поля (рис. П.4.6) нужные значения.
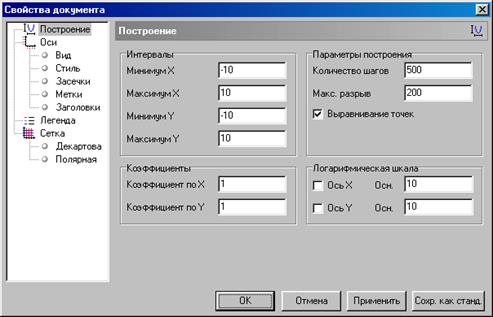
Рис. П.4.6. Изменение свойств графика в программе Advanced Grapher
Для построения графика по табличным данным щелкните по кнопке Добавить таблицу  , введите данные (рис. П.4.7) с использованием точки для разделения целой и дробной частей, поставьте флажок на поле Точки и щелкните ОК. Затем щелкните по кнопке Свойства документа
, введите данные (рис. П.4.7) с использованием точки для разделения целой и дробной частей, поставьте флажок на поле Точки и щелкните ОК. Затем щелкните по кнопке Свойства документа  и задайте интервалы по оси X и по оси Y (рис. П.4.6).
и задайте интервалы по оси X и по оси Y (рис. П.4.6).
Рассмотрим пример проведения через экспериментальные точки кривой заданного вида (это требуется в работе 4). После построения графика по табличным данным щелкните по кнопке + F (Добавить график), затем в диалоговом окне (см. рис. П.4.5) введите уравнение кривой (рис. П.4.8а). Для редактирования выражения щелкните по кнопке  и в диалоговом окне (рис. П.4.5) сделайте необходимые изменения так, чтобы кривая прошла максимально близко к экспериментальным точкам и оставляла выше и ниже от себя примерно одинаковое число точек с чередованием “выше-ниже” (рис. П.4.8 б).
и в диалоговом окне (рис. П.4.5) сделайте необходимые изменения так, чтобы кривая прошла максимально близко к экспериментальным точкам и оставляла выше и ниже от себя примерно одинаковое число точек с чередованием “выше-ниже” (рис. П.4.8 б).
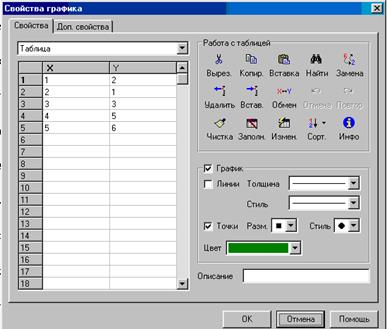
| Рис. П.4.7. Заполнение таблицы данным в программе Advanced Grapher
| 
|
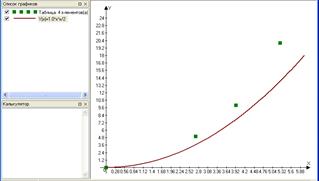
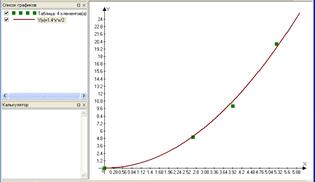
а б
Рис. П.4.8. Построения точек по табличным данным и сглаживающей кривой в программе Advanced Grapher
Приложение 5.
Метод наименьших квадратов и сглаживание данных
Важной задачей обработки результатов измерения, имеющих погрешности, является интерполирование со сглаживанием. Эта задача состоит в построении такой кривой, которая бы в известном смысле наилучшим образом аппроксимировала функцию 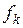 , заданную со случайными погрешностями в узловых точках
, заданную со случайными погрешностями в узловых точках 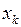 ,
, 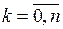 . Частой задачей физического практикума является проведение прямой
. Частой задачей физического практикума является проведение прямой
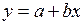 , (П.5.1)
, (П.5.1)
на плоскости (x,y) так, чтобы она проходила наиболее близко к экспериментальным точкам 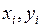 . Уравнение (П.5.1) описывает прямую регрессии* величины y, приближенно описывающую статистическую зависимость y от x [31, с. 553], величина b называется коэффициентом регрессия y на x. Минимизация среднеквадратичного отклонения
. Уравнение (П.5.1) описывает прямую регрессии* величины y, приближенно описывающую статистическую зависимость y от x [31, с. 553], величина b называется коэффициентом регрессия y на x. Минимизация среднеквадратичного отклонения
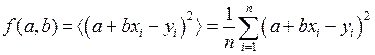 , (П.5.2)
, (П.5.2)
в случае линейной средней квадратической регрессии дает формулы для определения коэффициентов a, b
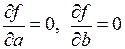 , (П.5.3)
, (П.5.3)
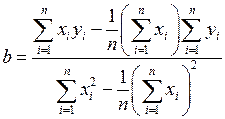 ,
, 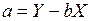 , (П.5.4)
, (П.5.4)
где
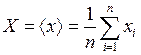 ,
, 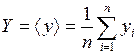 . (П.5.5)
. (П.5.5)
Наименьшее значение среднего квадрата отклонения (остаточная дисперсия) равна
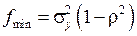 ,
, 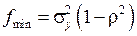 . (П.5.6)
. (П.5.6)
где 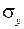 - дисперсия величины y
- дисперсия величины y
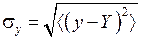 ,
, 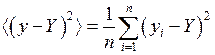 , (П.5.7)
, (П.5.7)
r - коэффициент корреляции (взаимосвязи) x и y
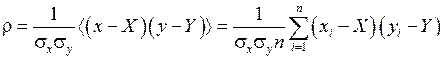 , (П.5.8)
, (П.5.8)
где 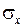 - дисперсия величины x
- дисперсия величины x
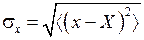 ,
, 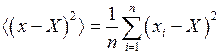 . (П.5.9)
. (П.5.9)
Эти формулы реализованы во многих программах научной графики и обработки данных. Рассмотрим несколько примеров.
В программе MicroCal Origin 3.0 для проведения сглаживающей прямой при выделенном графике следует выполнить команду Fit - Linear Regression (Сглаживание-Линейная регрессия), пример показан на рис. П.5.1.

Рис. П.5.1. Пример сглаживания данных (линейная регрессия y на x) в программе MicroCal Origin 3.0
Уравнение прямой и значения его коэффициентов A = a и B = b в столбце “Value” окна Script Window. В столбце “sd” приведены стандартные погрешности величин a, b, далее даны коэффициент корреляции R, стандартное отклонение SD (standard deviation),
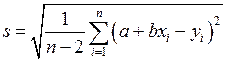 , (П.5.10)
, (П.5.10)
число N точек и вероятность Р того, что R = 0, т.е. того, что величины y и x независимы.
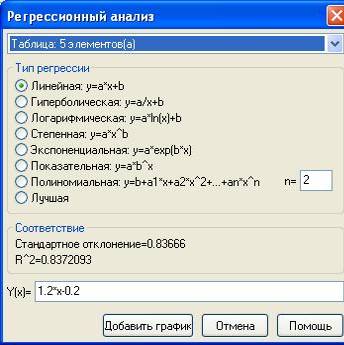
В программе Advanced Grapher (см. Прил. 3) для проведения сглаживающей прямой при выделенном графике следует выполнить команду Вычисления-Регрессионный анализ… . В окне регрессионного анализа (рис. П.5.2а) по умолчанию установлен режим линейной регрессии, выводится уравнение прямой и значения стандартного отклонения, вычисленного по формуле
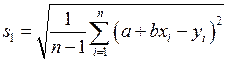 , (П.5.10)
, (П.5.10)
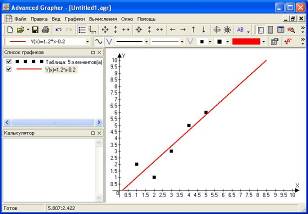
и квадрата коэффициента корреляции 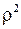 , график показан на рис. П.5.2б.
, график показан на рис. П.5.2б.
а б
Рис. П.5.2. Пример сглаживания данных (линейная регрессия y на x) в программе Advanced Grapher: а - параметры регрессии, б - график
В программе OpenOffice.org Calc для проведения сглаживающей прямой следует выделить маркеры точек графика щелчком по одному из них левой кнопкой мыши, затем щелкнуть правой кнопкой мыши и в контекстном





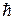 =1, масса электрона
=1, масса электрона 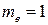 , единицей длины служит Боровский радиус
, единицей длины служит Боровский радиус 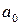 , равный 0.0529 нм, единицей энергии служит величина, равная 27.21 эВ (удвоенному значению энергии состояния 1s атома водорода). Данные для расчета вносятся в текстовый файл input . txt:
, равный 0.0529 нм, единицей энергии служит величина, равная 27.21 эВ (удвоенному значению энергии состояния 1s атома водорода). Данные для расчета вносятся в текстовый файл input . txt: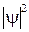 и потенциального барьера и зависимости D(E) выводятся на экран (см. рис. 17.11).
и потенциального барьера и зависимости D(E) выводятся на экран (см. рис. 17.11).
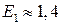 , квадрат модуля волновой функции (а) и зависимость проницаемости D барьера от энергии E (б)
, квадрат модуля волновой функции (а) и зависимость проницаемости D барьера от энергии E (б)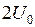 . Постройте вручную или на компьютере с помощью программы Origin зависимости D(E).
. Постройте вручную или на компьютере с помощью программы Origin зависимости D(E). (рис. 17.12). Получите на экране изображение квадрата модуля волновой функции для энергии электрона много меньше уровня
(рис. 17.12). Получите на экране изображение квадрата модуля волновой функции для энергии электрона много меньше уровня 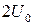 , она сохраняется в файле result.txt. Постройте вручную или на компьютере с помощью программы Origin зависимости D(E). В программе Origin выполните команду File-Import-ASCII, в диалоговом окне укажите путь к файлу, щелкните ОК. Найдите на графике характерные участки возрастания и убывания D(E) вблизи
, она сохраняется в файле result.txt. Постройте вручную или на компьютере с помощью программы Origin зависимости D(E). В программе Origin выполните команду File-Import-ASCII, в диалоговом окне укажите путь к файлу, щелкните ОК. Найдите на графике характерные участки возрастания и убывания D(E) вблизи 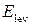 , а также возрастания D(E) при
, а также возрастания D(E) при 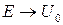 . Пример показан на рис. 17.12. Сопоставьте этим участкам участки ВАХ туннельного диода.
. Пример показан на рис. 17.12. Сопоставьте этим участкам участки ВАХ туннельного диода.





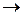 О2+Х, (П2.1)
О2+Х, (П2.1)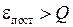 . Для этого температура газа Т должна быть достаточно высокой, Т > 550 К, чтобы средняя кинетическая энергия атомов превышала порог реакции
. Для этого температура газа Т должна быть достаточно высокой, Т > 550 К, чтобы средняя кинетическая энергия атомов превышала порог реакции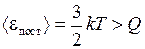 , (П2.3)
, (П2.3)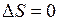 , где S - спин атома. Поэтому такое состояние является долгоживущим (метастабильным). Атом кислорода, находящийся длительное время в возбужденном состоянии 1D, может столкнуться с молекулой водорода и вызвать протекание экзотермической реакции (идущей с выделением энергии
, где S - спин атома. Поэтому такое состояние является долгоживущим (метастабильным). Атом кислорода, находящийся длительное время в возбужденном состоянии 1D, может столкнуться с молекулой водорода и вызвать протекание экзотермической реакции (идущей с выделением энергии 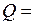 1.97 эВ)
1.97 эВ)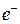
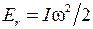 вращения с угловой скоростью w молекулы ОН с моментом инерции I. Пусть молекула воды до столкновения покоилась, тогда из закона сохранения импульса следует,
вращения с угловой скоростью w молекулы ОН с моментом инерции I. Пусть молекула воды до столкновения покоилась, тогда из закона сохранения импульса следует,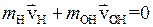 ,
, 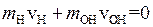 . (П2.8)
. (П2.8)
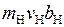 . Вследствие закона сохранения момента импульса модуль момента импульса молекулы ОН с моментом инерции I равен
. Вследствие закона сохранения момента импульса модуль момента импульса молекулы ОН с моментом инерции I равен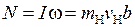 . (П2.9)
. (П2.9)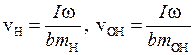 . (П2.10)
. (П2.10)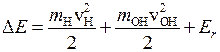 . (П2.11)
. (П2.11)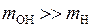 и выражения для момента инерции
и выражения для момента инерции 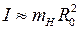 , получим
, получим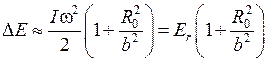 . (П2.12)
. (П2.12)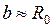 можно увидеть, что во вращательную энергию переходит примерно половина всего приращения кинетической энергии системы.
можно увидеть, что во вращательную энергию переходит примерно половина всего приращения кинетической энергии системы.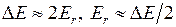 . (П2.13)
. (П2.13)
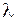 . Зависимость
. Зависимость 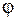 называется градуировочной кривой (градуировочным графиком), с ее помощью определяют длины волн
называется градуировочной кривой (градуировочным графиком), с ее помощью определяют длины волн 

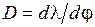 называется угловой дисперсией монохроматора. В красно-оранжевой области спектра величина дисперсии велика, поэтому для градуировки необходимо использовать больше линий (из спектра неона), чем в остальных участках спектра. Изображение фотопластинки со спектром неоновой лампы и схема расположения спектральных линий показаны на рис. П3.4.
называется угловой дисперсией монохроматора. В красно-оранжевой области спектра величина дисперсии велика, поэтому для градуировки необходимо использовать больше линий (из спектра неона), чем в остальных участках спектра. Изображение фотопластинки со спектром неоновой лампы и схема расположения спектральных линий показаны на рис. П3.4.

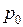 , при котором градуировочный график l = l(j) будет достаточно гладкой линией, см. рис. П3.5. При этом необязательно использовать все линии неона из табл. П3.1.
, при котором градуировочный график l = l(j) будет достаточно гладкой линией, см. рис. П3.5. При этом необязательно использовать все линии неона из табл. П3.1.


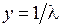 . Для этого в рабочей области выделите столбец, содержащий значения длин волн, выполните команду Edit - Insert (Редактировать-Вставить). Выделите новый столбец, выполните команду Data - Set Column Values … (Данные-Установить значения для колонки). В диалоговом окне введите формулу для вычисления обратных значений (рис. П4.3), щелкните по кнопке Do it (Сделать это).
. Для этого в рабочей области выделите столбец, содержащий значения длин волн, выполните команду Edit - Insert (Редактировать-Вставить). Выделите новый столбец, выполните команду Data - Set Column Values … (Данные-Установить значения для колонки). В диалоговом окне введите формулу для вычисления обратных значений (рис. П4.3), щелкните по кнопке Do it (Сделать это).

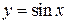
 (см. рис. П.4.5) и в диалоговом окне (рис. П.4.6) сделайте необходимые изменения.
(см. рис. П.4.5) и в диалоговом окне (рис. П.4.6) сделайте необходимые изменения.
 (см. рис. П.4.5) и введите в поля (рис. П.4.6) нужные значения.
(см. рис. П.4.5) и введите в поля (рис. П.4.6) нужные значения.
 , введите данные (рис. П.4.7) с использованием точки для разделения целой и дробной частей, поставьте флажок на поле Точки и щелкните ОК. Затем щелкните по кнопке Свойства документа
, введите данные (рис. П.4.7) с использованием точки для разделения целой и дробной частей, поставьте флажок на поле Точки и щелкните ОК. Затем щелкните по кнопке Свойства документа  и задайте интервалы по оси X и по оси Y (рис. П.4.6).
и задайте интервалы по оси X и по оси Y (рис. П.4.6).


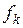 , заданную со случайными погрешностями в узловых точках
, заданную со случайными погрешностями в узловых точках 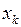 ,
, 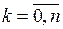 . Частой задачей физического практикума является проведение прямой
. Частой задачей физического практикума является проведение прямой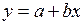 , (П.5.1)
, (П.5.1)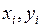 . Уравнение (П.5.1) описывает прямую регрессии* величины y, приближенно описывающую статистическую зависимость y от x [31, с. 553], величина b называется коэффициентом регрессия y на x. Минимизация среднеквадратичного отклонения
. Уравнение (П.5.1) описывает прямую регрессии* величины y, приближенно описывающую статистическую зависимость y от x [31, с. 553], величина b называется коэффициентом регрессия y на x. Минимизация среднеквадратичного отклонения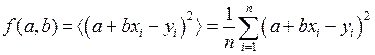 , (П.5.2)
, (П.5.2)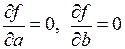 , (П.5.3)
, (П.5.3)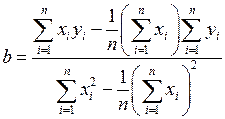 ,
, 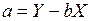 , (П.5.4)
, (П.5.4)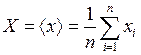 ,
, 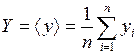 . (П.5.5)
. (П.5.5)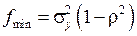 ,
, 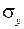 - дисперсия величины y
- дисперсия величины y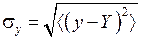 ,
, 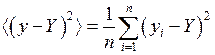 , (П.5.7)
, (П.5.7)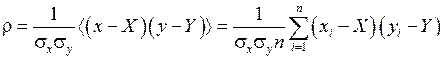 , (П.5.8)
, (П.5.8)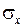 - дисперсия величины x
- дисперсия величины x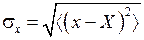 ,
, 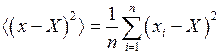 . (П.5.9)
. (П.5.9)
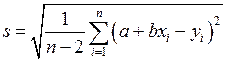 , (П.5.10)
, (П.5.10)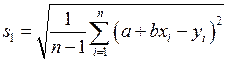 , (П.5.10)
, (П.5.10)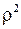 , график показан на рис. П.5.2б.
, график показан на рис. П.5.2б.




