Рассмотрим физические механизмы объемной и контактной составляющих термо-э.д.с. на примере однородного проводника (рис. 14.4), на концах которого поддерживается разность температур 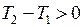 , так что вдоль проводника существует градиент температуры
, так что вдоль проводника существует градиент температуры 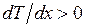 .
.
 а
а
 б
б
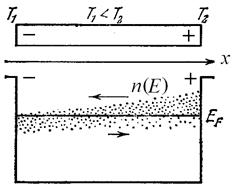
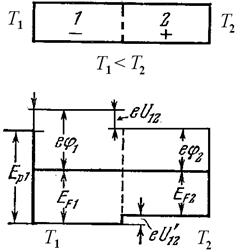
| Рис. 14.3. Упрощенная схема возникновения термо-э.д.с. в однородном проводнике: (а) – диффузия электронов с энергиями больше и меньше энергии Ферми 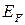 ; (б) – сравнение свойств металла на холодном (слева) и горячем (справа) концах: ; (б) – сравнение свойств металла на холодном (слева) и горячем (справа) концах: 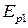 – потенциальная энергия при – потенциальная энергия при 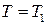 , , 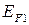 , , 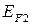 – энергии Ферми при температурах – энергии Ферми при температурах 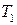 и и 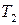 , , 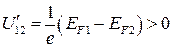 – внутренняя контактная разность потенциалов, – внутренняя контактная разность потенциалов, 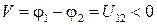 – термо-э.д.с. – термо-э.д.с.
|
Уровень Ферми в более холодном образце металла лежит, согласно формуле (П7.15), выше, чем в более горячем образце того же металла. При возникновении контакта между холодным и горячим образцами металла электроны с самых высоких уровней холодного конца металла в ходе хаотического движения могут занимать места на более низких свободных уровнях горячего конца металла до тех пор, пока уровни Ферми на обоих концах (и холодном, и горячем) не сравняются. В результате, если бы не было никаких других процессов, холодный конец металла приобрел бы положительный заряд, его потенциал возрос бы. Горячий конец приобрел бы избыточный отрицательный заряд, его потенциал уменьшился бы. Соответственно потенциальная энергия электрона на холодном конце металла должна была бы уменьшиться, а на горячем увеличиться. Возникшее электрическое поле остановило бы переходы электронов с холодного конца на горячий после выравнивания уровней Ферми на обоих концах и наступления равновесия. При равновесии в проводнике на рис. 14.4 уровень Ферми (химический потенциал) одинаков у обоих концов проводника (и горячего, и холодного). Меньшее значение энергии Ферми на более нагретом конце приводит к внутренней контактной разности потенциалов 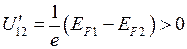 .
.
Носители тока (в металлах – электроны), сосредоточенные на горячем конце, обладают большей энергией и большей скоростью движения по сравнению с носителями холодного конца. Поэтому в проводнике от горячего конца к холодному установится поток носителей тока, приводящий к перераспределению зарядов на концах проводника. В более точной модели диффузия электронов рассматривается с учетом их энергий. Концентрация электронов с 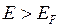 у нагретого конца будет больше, чем у холодного; концентрация электронов с
у нагретого конца будет больше, чем у холодного; концентрация электронов с 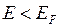 будет, наоборот, у нагретого конца меньше. Вдоль проводника возникнет градиент концентрации электронов с данным значением энергии (см. рис. 14.4а), что повлечет за собой диффузию более быстрых электронов к холодному концу, а более медленных — к теплому. Диффузионный поток быстрых электронов будет больше, чем поток медленных электронов. Поэтому вблизи холодного конца образуется избыток электронов, а вблизи горячего — их недостаток. Это приводит к возникновению диффузионного (объемного) слагаемого термо-э.д.с.
будет, наоборот, у нагретого конца меньше. Вдоль проводника возникнет градиент концентрации электронов с данным значением энергии (см. рис. 14.4а), что повлечет за собой диффузию более быстрых электронов к холодному концу, а более медленных — к теплому. Диффузионный поток быстрых электронов будет больше, чем поток медленных электронов. Поэтому вблизи холодного конца образуется избыток электронов, а вблизи горячего — их недостаток. Это приводит к возникновению диффузионного (объемного) слагаемого термо-э.д.с.
При равновесии в проводнике на рис. 14.4 уровень Ферми (химический потенциал) одинаков у обоих концов проводника (и горячего, и холодного). Но меньшее значение энергии Ферми 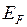 (максимальной кинетической энергии электронов) на более нагретом конце приводит к внутренней контактной разности потенциалов
(максимальной кинетической энергии электронов) на более нагретом конце приводит к внутренней контактной разности потенциалов 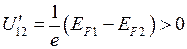 , которая направлена противоположно объемной (диффузионной) и фононной составляющим. Накопление противоположных зарядов на концах проводника, вызванное преобладающими диффузионными и фононными токами, будет продолжаться до тех пор, пока возникшая разность потенциалов не вызовет уравновешивающий их обратный поток электронов. Следовательно, потенциал
, которая направлена противоположно объемной (диффузионной) и фононной составляющим. Накопление противоположных зарядов на концах проводника, вызванное преобладающими диффузионными и фононными токами, будет продолжаться до тех пор, пока возникшая разность потенциалов не вызовет уравновешивающий их обратный поток электронов. Следовательно, потенциал 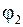 горячего конца электронного проводника будет выше потенциала
горячего конца электронного проводника будет выше потенциала 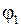 холодного конца. Обобщенный закон Ома для проводника в этом случае
холодного конца. Обобщенный закон Ома для проводника в этом случае
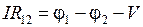 , (14.3)
, (14.3)
где 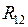 − сопротивление, I − ток, V − термо-э.д.с., и за положительное направление принято направление от горячего конца к холодному. Поскольку ток равен нулю
− сопротивление, I − ток, V − термо-э.д.с., и за положительное направление принято направление от горячего конца к холодному. Поскольку ток равен нулю 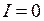
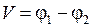 , (14.4)
, (14.4)
Термо-э.д.с. отрицательна для нормального проводника со свободными электронами (при 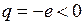 )
)
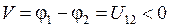 . (14.5)
. (14.5)
В случае проводника с положительными свободными зарядами 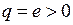 их больший диффузионный поток от горячего конца приведет к избытку отрицательного заряда на этом конце, потенциалам
их больший диффузионный поток от горячего конца приведет к избытку отрицательного заряда на этом конце, потенциалам 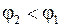 и положительной термо-э.д.с.
и положительной термо-э.д.с.
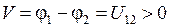 . (14.6)
. (14.6)
Равновесному состоянию отвечает нулевая полная плотность тока в проводнике
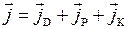 . (14.7)
. (14.7)
Таким образом, в проводнике между отрицательно заряженным холодным концом и положительно заряженным горячим возникает электрическое поле с напряженностью 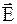 и разностью потенциалов
и разностью потенциалов 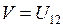 , определяемой из условия (14.7) с учетом свойств электронов в металле (их подвижностью, длиной свободного пробега, временем релаксации, формой поверхности Ферми и т.д.). В полупроводниках дополнительно следует учитывать возрастание концентрации носителей заряда (свободных электронов и дырок) с ростом температуры (см. работу 15). В собственном полупроводнике (см. работу 15) направления диффузии электронов и дырок противоположны, вследствие равенства их концентраций полная термо-э.д.с. равна нулю.
, определяемой из условия (14.7) с учетом свойств электронов в металле (их подвижностью, длиной свободного пробега, временем релаксации, формой поверхности Ферми и т.д.). В полупроводниках дополнительно следует учитывать возрастание концентрации носителей заряда (свободных электронов и дырок) с ростом температуры (см. работу 15). В собственном полупроводнике (см. работу 15) направления диффузии электронов и дырок противоположны, вследствие равенства их концентраций полная термо-э.д.с. равна нулю.
Точное вычисление плотностей тока в (14.7) и величины термо-э.д.с. представляет собой сложную задачу (подробнее см. [27]). Приблизительную оценку объемного (диффузионного) и контактного вкладов в величины термо-э.д.с. и удельной термо-э.д.с. можно сделать, заменив условие (14.7) равенства нулю полного тока, на условие равновесия носителей заряда (электронов, дырок) в проводнике. Рассмотрим в проводнике малый элемент объема в виде куба с ребрами dx=dy=dz, параллельными осям координат (см. рис. 14.5).
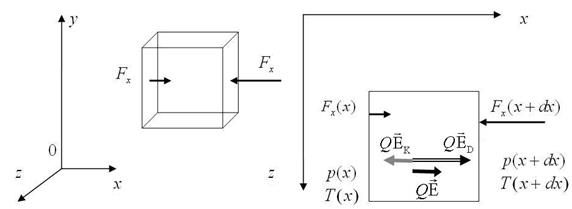
Рис. 14.4. Применение условия равновесия носителей заряда для однородного металлического проводника с градиентом температуры 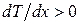 .
.
Электронный газ создает в проводнике давление (аналогичная формула имеет место для идеального газа)
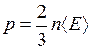 , (14.8)
, (14.8)
где 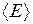 − средняя энергия электронов в проводнике, n − их концентрация. Температура и давление у правой грани куба T(x+dx), p(x+dx) соответственно выше, чем значения T(x) и p(x) у левой грани. На правую и левую грани куба действуют силы давления (тонкие стрелки на рис. 14.5) с проекциями на ось x, равными соответственно
− средняя энергия электронов в проводнике, n − их концентрация. Температура и давление у правой грани куба T(x+dx), p(x+dx) соответственно выше, чем значения T(x) и p(x) у левой грани. На правую и левую грани куба действуют силы давления (тонкие стрелки на рис. 14.5) с проекциями на ось x, равными соответственно 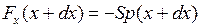 и
и 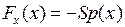 , где
, где 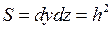 − площадь грани куба. Из-за разности давлений слева и справа от куба на него действует направленная влево равнодействующая сил давления с проекцией
− площадь грани куба. Из-за разности давлений слева и справа от куба на него действует направленная влево равнодействующая сил давления с проекцией
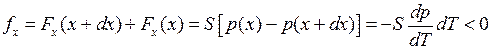 . (14.9)
. (14.9)
Из-за разделения зарядов в проводнике внутри куба существует электрическое поле: объемная составляющая вектора напряженности 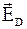 , обусловленная диффузией электронов, контактная составляющая
, обусловленная диффузией электронов, контактная составляющая 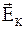 , обусловленная температурной зависимостью энергии Ферми, и их суперпозиция
, обусловленная температурной зависимостью энергии Ферми, и их суперпозиция 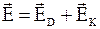 . На находящиеся в кубе носители заряда (например, электроны с зарядом q=−e) с концентрацией n=const и полным зарядом Q=qnSdx со стороны электрического поля действуют направленная вправо сила с проекцией
. На находящиеся в кубе носители заряда (например, электроны с зарядом q=−e) с концентрацией n=const и полным зарядом Q=qnSdx со стороны электрического поля действуют направленная вправо сила с проекцией 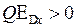 (см. рис. 14.4) и направленная влево сила с проекцией
(см. рис. 14.4) и направленная влево сила с проекцией 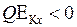 . Проекция результирующей силы (черная стрелка на рис. 14.4) равна
. Проекция результирующей силы (черная стрелка на рис. 14.4) равна
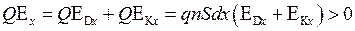 . (14.10)
. (14.10)
Условие равновесия электронов в кубе 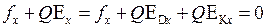 дает
дает
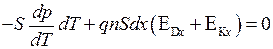 . (14.11)
. (14.11)
Напряженности электрических полей связаны с разностями потенциалов: 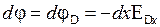 ,
, 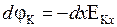 , поэтому
, поэтому
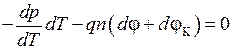 . (14.12)
. (14.12)
Для обусловленной диффузионным (объемным) перераспределением зарядов термо-э.д.с. (без учета увлечения электронов фононами)
dV = j(x) − j(x+dx) = −dj, (14.13),
для обусловленной контактным перераспределением зарядов термо-э.д.с. 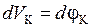 , поэтому
, поэтому
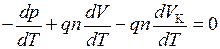 . (14.14)
. (14.14)
Для вычисления удельной термо-э.д.с. металла
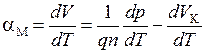 . (14.15)
. (14.15)
используем температурные зависимости средней энергии электронов (П7.16) и энергии Ферми (П7.15) из Прил. 7. Вычисляя производные, получим
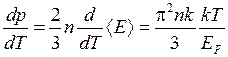 , (14.16)
, (14.16)
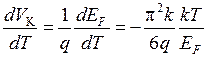 , (14.17)
, (14.17)
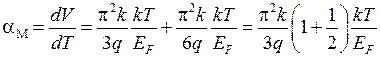 . (14.18)
. (14.18)
Более строгий расчет для металлов, длина свободного пробега электронов в которых зависит от их энергии по закону 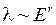 , приводит к выражению
, приводит к выражению
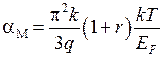 . (14.19)
. (14.19)
При T®0 объемный и контактные вклады в термо-э.д.с. также стремятся к нулю и основным является механизм увлечения носителей заряда фононами, удельная термо-э.д.с. которого при этом растет.
Для большинства металлов r>0 и (поскольку q<0) 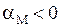 , поэтому горячий конец металла приобретает положительный заряд, а холодный конец – отрицательный заряд. Иногда более быстрые электроны обладают меньшим коэффициентом диффузии и меньшей длиной свободного пробега, в этом случае r<0 и термо-э.д.с. может иметь противоположный знак
, поэтому горячий конец металла приобретает положительный заряд, а холодный конец – отрицательный заряд. Иногда более быстрые электроны обладают меньшим коэффициентом диффузии и меньшей длиной свободного пробега, в этом случае r<0 и термо-э.д.с. может иметь противоположный знак 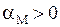 . В этом случае электроны с большей энергией должны диффундировать медленнее, чем электроны, имеющие более низкую энергию. Диффузионный поток электронов (см. рис. 14.3) в этом случае окажется направленным от холодного конца в горячему, вследствие чего знак объемной составляющей термо-э.д.с. изменится на обратный. Это может привести к изменению знака термо-э.д.с. проводника в целом. Такая картина наблюдается, в частности, в ряде переходных металлов и сплавов.
. В этом случае электроны с большей энергией должны диффундировать медленнее, чем электроны, имеющие более низкую энергию. Диффузионный поток электронов (см. рис. 14.3) в этом случае окажется направленным от холодного конца в горячему, вследствие чего знак объемной составляющей термо-э.д.с. изменится на обратный. Это может привести к изменению знака термо-э.д.с. проводника в целом. Такая картина наблюдается, в частности, в ряде переходных металлов и сплавов.
Формула (14.19) справедлива для металлов с квадратичной зависимостью энергии 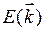 от волнового вектора
от волнового вектора 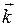 . В металлах и сплавах, обладающих сложной поверхностью Ферми, вклад в термо-э.д.с. различных участков этой поверхности может быть различен не только по значению, но и по знаку, вследствие чего термо-э.д.с. проводника в целом может быть равна или близка к нулю.
. В металлах и сплавах, обладающих сложной поверхностью Ферми, вклад в термо-э.д.с. различных участков этой поверхности может быть различен не только по значению, но и по знаку, вследствие чего термо-э.д.с. проводника в целом может быть равна или близка к нулю.
Градуировка термопары
Для изучения температурной зависимости термо-э.д.с. термопары используются сосуд, водонагреватель (электрочайник) и термометр. Один конец термопары помещается в сосуд, куда наливается вода. Второй конец термопары находится при комнатной температуре. Измерьте ее термометром до выполнения основных измерений. Температура воды 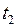 в сосуде измеряется термометром, измерение термо-э.д.с. V выполняется с помощью цифрового милливольтметра (мультиметра). Подключите термопару к гнездам милливольтметра, измерьте мультиметром комнатную температуру. Сравните полученное значение с показанием термометра.
в сосуде измеряется термометром, измерение термо-э.д.с. V выполняется с помощью цифрового милливольтметра (мультиметра). Подключите термопару к гнездам милливольтметра, измерьте мультиметром комнатную температуру. Сравните полученное значение с показанием термометра.
Перед выполнением работы требуется подготовить кубики льда и водонагреватель (электрочайник) с водой температуры около 70ºС. Выполните измерения в следующем порядке.
1. Налейте на дно сосуда слой холодной воды (примерно 2 см) и положите кубики льда, так, чтобы участок термопарой и носик термометра были полностью под водой. Когда показания термометра и милливольтметра установятся, внесите их в табл. 14.2. При этом значения термо-э.д.с. должны быть отрицательными.
Таблица 14.2
| №
| t, ºС
| 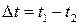 , ºС , ºС
| V, мВ
|
| 1
|
|
|
|
| …
|
|
|
|
| 7-8
|
|
|
|
2. Добавляя понемногу воду из чайника, повышайте температуру воды в сосуде в среднем примерно на 10±5ºС. Когда показания термометра и милливольтметра установятся, внесите их в табл. 14.2. Последнее значение температуры должно соответствовать максимальной температуре несколько меньшей 60ºС.
3. Постройте график зависимости V от 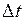 . Определите значение коэффициента удельной термо-э.д.с. a для данной пары проводников, из которых изготовлена термопара.
. Определите значение коэффициента удельной термо-э.д.с. a для данной пары проводников, из которых изготовлена термопара.
Контрольные вопросы
1. Расскажите о распределении Ферми для электронов в металлах.
2. Расскажите об энергии Ферми для электронов в металлах и ее температурной зависимости.
3. Расскажите о контактной разности потенциалов.
4. Расскажите о причинах возникновения термо-э.д.с. в металлах.
5. Расскажите о свойствах и применении термопар.
Лабораторная работа № 15.
Температурная зависимость проводимости полупроводников
Цель работы: изучение зависимости собственной и примесной проводимости полупроводников от температуры. Нахождение зависимости сопротивления полупроводников – термисторов от температуры, вычисление энергии активации и ширины запрещенной зоны полупроводника.
Приборы и принадлежности: термистор, омметр, водонагреватель, холодильник.
Образование энергетических зон в кристаллах





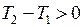 , так что вдоль проводника существует градиент температуры
, так что вдоль проводника существует градиент температуры 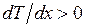 .
. а
а
 б
б
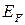 ; (б) – сравнение свойств металла на холодном (слева) и горячем (справа) концах:
; (б) – сравнение свойств металла на холодном (слева) и горячем (справа) концах: 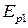 – потенциальная энергия при
– потенциальная энергия при 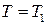 ,
, 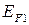 ,
, 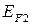 – энергии Ферми при температурах
– энергии Ферми при температурах 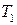 и
и 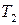 ,
, 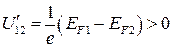 – внутренняя контактная разность потенциалов,
– внутренняя контактная разность потенциалов, 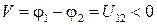 – термо-э.д.с.
– термо-э.д.с.
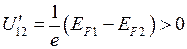 .
.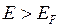 у нагретого конца будет больше, чем у холодного; концентрация электронов с
у нагретого конца будет больше, чем у холодного; концентрация электронов с 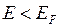 будет, наоборот, у нагретого конца меньше. Вдоль проводника возникнет градиент концентрации электронов с данным значением энергии (см. рис. 14.4а), что повлечет за собой диффузию более быстрых электронов к холодному концу, а более медленных — к теплому. Диффузионный поток быстрых электронов будет больше, чем поток медленных электронов. Поэтому вблизи холодного конца образуется избыток электронов, а вблизи горячего — их недостаток. Это приводит к возникновению диффузионного (объемного) слагаемого термо-э.д.с.
будет, наоборот, у нагретого конца меньше. Вдоль проводника возникнет градиент концентрации электронов с данным значением энергии (см. рис. 14.4а), что повлечет за собой диффузию более быстрых электронов к холодному концу, а более медленных — к теплому. Диффузионный поток быстрых электронов будет больше, чем поток медленных электронов. Поэтому вблизи холодного конца образуется избыток электронов, а вблизи горячего — их недостаток. Это приводит к возникновению диффузионного (объемного) слагаемого термо-э.д.с.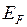 (максимальной кинетической энергии электронов) на более нагретом конце приводит к внутренней контактной разности потенциалов
(максимальной кинетической энергии электронов) на более нагретом конце приводит к внутренней контактной разности потенциалов 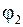 горячего конца электронного проводника будет выше потенциала
горячего конца электронного проводника будет выше потенциала 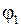 холодного конца. Обобщенный закон Ома для проводника в этом случае
холодного конца. Обобщенный закон Ома для проводника в этом случае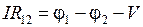 , (14.3)
, (14.3)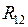 − сопротивление, I − ток, V − термо-э.д.с., и за положительное направление принято направление от горячего конца к холодному. Поскольку ток равен нулю
− сопротивление, I − ток, V − термо-э.д.с., и за положительное направление принято направление от горячего конца к холодному. Поскольку ток равен нулю 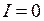
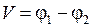 , (14.4)
, (14.4)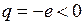 )
)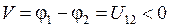 . (14.5)
. (14.5)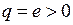 их больший диффузионный поток от горячего конца приведет к избытку отрицательного заряда на этом конце, потенциалам
их больший диффузионный поток от горячего конца приведет к избытку отрицательного заряда на этом конце, потенциалам 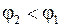 и положительной термо-э.д.с.
и положительной термо-э.д.с.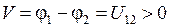 . (14.6)
. (14.6)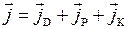 . (14.7)
. (14.7)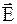 и разностью потенциалов
и разностью потенциалов 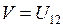 , определяемой из условия (14.7) с учетом свойств электронов в металле (их подвижностью, длиной свободного пробега, временем релаксации, формой поверхности Ферми и т.д.). В полупроводниках дополнительно следует учитывать возрастание концентрации носителей заряда (свободных электронов и дырок) с ростом температуры (см. работу 15). В собственном полупроводнике (см. работу 15) направления диффузии электронов и дырок противоположны, вследствие равенства их концентраций полная термо-э.д.с. равна нулю.
, определяемой из условия (14.7) с учетом свойств электронов в металле (их подвижностью, длиной свободного пробега, временем релаксации, формой поверхности Ферми и т.д.). В полупроводниках дополнительно следует учитывать возрастание концентрации носителей заряда (свободных электронов и дырок) с ростом температуры (см. работу 15). В собственном полупроводнике (см. работу 15) направления диффузии электронов и дырок противоположны, вследствие равенства их концентраций полная термо-э.д.с. равна нулю.
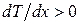 .
.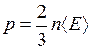 , (14.8)
, (14.8)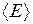 − средняя энергия электронов в проводнике, n − их концентрация. Температура и давление у правой грани куба T(x+dx), p(x+dx) соответственно выше, чем значения T(x) и p(x) у левой грани. На правую и левую грани куба действуют силы давления (тонкие стрелки на рис. 14.5) с проекциями на ось x, равными соответственно
− средняя энергия электронов в проводнике, n − их концентрация. Температура и давление у правой грани куба T(x+dx), p(x+dx) соответственно выше, чем значения T(x) и p(x) у левой грани. На правую и левую грани куба действуют силы давления (тонкие стрелки на рис. 14.5) с проекциями на ось x, равными соответственно 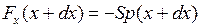 и
и 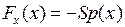 , где
, где 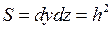 − площадь грани куба. Из-за разности давлений слева и справа от куба на него действует направленная влево равнодействующая сил давления с проекцией
− площадь грани куба. Из-за разности давлений слева и справа от куба на него действует направленная влево равнодействующая сил давления с проекцией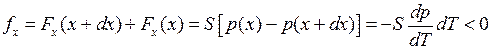 . (14.9)
. (14.9)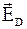 , обусловленная диффузией электронов, контактная составляющая
, обусловленная диффузией электронов, контактная составляющая 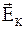 , обусловленная температурной зависимостью энергии Ферми, и их суперпозиция
, обусловленная температурной зависимостью энергии Ферми, и их суперпозиция 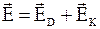 . На находящиеся в кубе носители заряда (например, электроны с зарядом q=−e) с концентрацией n=const и полным зарядом Q=qnSdx со стороны электрического поля действуют направленная вправо сила с проекцией
. На находящиеся в кубе носители заряда (например, электроны с зарядом q=−e) с концентрацией n=const и полным зарядом Q=qnSdx со стороны электрического поля действуют направленная вправо сила с проекцией 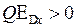 (см. рис. 14.4) и направленная влево сила с проекцией
(см. рис. 14.4) и направленная влево сила с проекцией 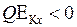 . Проекция результирующей силы (черная стрелка на рис. 14.4) равна
. Проекция результирующей силы (черная стрелка на рис. 14.4) равна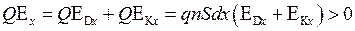 . (14.10)
. (14.10)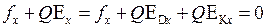 дает
дает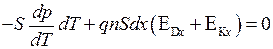 . (14.11)
. (14.11)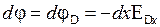 ,
, 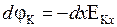 , поэтому
, поэтому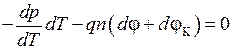 . (14.12)
. (14.12)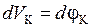 , поэтому
, поэтому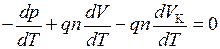 . (14.14)
. (14.14)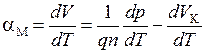 . (14.15)
. (14.15)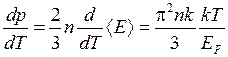 , (14.16)
, (14.16)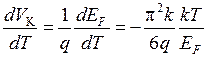 , (14.17)
, (14.17)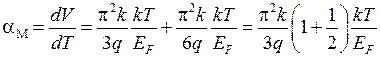 . (14.18)
. (14.18)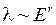 , приводит к выражению
, приводит к выражению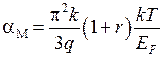 . (14.19)
. (14.19)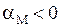 , поэтому горячий конец металла приобретает положительный заряд, а холодный конец – отрицательный заряд. Иногда более быстрые электроны обладают меньшим коэффициентом диффузии и меньшей длиной свободного пробега, в этом случае r<0 и термо-э.д.с. может иметь противоположный знак
, поэтому горячий конец металла приобретает положительный заряд, а холодный конец – отрицательный заряд. Иногда более быстрые электроны обладают меньшим коэффициентом диффузии и меньшей длиной свободного пробега, в этом случае r<0 и термо-э.д.с. может иметь противоположный знак 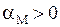 . В этом случае электроны с большей энергией должны диффундировать медленнее, чем электроны, имеющие более низкую энергию. Диффузионный поток электронов (см. рис. 14.3) в этом случае окажется направленным от холодного конца в горячему, вследствие чего знак объемной составляющей термо-э.д.с. изменится на обратный. Это может привести к изменению знака термо-э.д.с. проводника в целом. Такая картина наблюдается, в частности, в ряде переходных металлов и сплавов.
. В этом случае электроны с большей энергией должны диффундировать медленнее, чем электроны, имеющие более низкую энергию. Диффузионный поток электронов (см. рис. 14.3) в этом случае окажется направленным от холодного конца в горячему, вследствие чего знак объемной составляющей термо-э.д.с. изменится на обратный. Это может привести к изменению знака термо-э.д.с. проводника в целом. Такая картина наблюдается, в частности, в ряде переходных металлов и сплавов.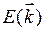 от волнового вектора
от волнового вектора 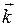 . В металлах и сплавах, обладающих сложной поверхностью Ферми, вклад в термо-э.д.с. различных участков этой поверхности может быть различен не только по значению, но и по знаку, вследствие чего термо-э.д.с. проводника в целом может быть равна или близка к нулю.
. В металлах и сплавах, обладающих сложной поверхностью Ферми, вклад в термо-э.д.с. различных участков этой поверхности может быть различен не только по значению, но и по знаку, вследствие чего термо-э.д.с. проводника в целом может быть равна или близка к нулю.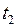 в сосуде измеряется термометром, измерение термо-э.д.с. V выполняется с помощью цифрового милливольтметра (мультиметра). Подключите термопару к гнездам милливольтметра, измерьте мультиметром комнатную температуру. Сравните полученное значение с показанием термометра.
в сосуде измеряется термометром, измерение термо-э.д.с. V выполняется с помощью цифрового милливольтметра (мультиметра). Подключите термопару к гнездам милливольтметра, измерьте мультиметром комнатную температуру. Сравните полученное значение с показанием термометра.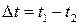 , ºС
, ºС
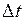 . Определите значение коэффициента удельной термо-э.д.с. a для данной пары проводников, из которых изготовлена термопара.
. Определите значение коэффициента удельной термо-э.д.с. a для данной пары проводников, из которых изготовлена термопара.

