Энергия молекулы 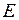 может быть приближенно представлена суммой трех энергий: электронной
может быть приближенно представлена суммой трех энергий: электронной 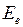 , колебательной
, колебательной 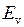 (индекс v от англ. vibration – колебание) и вращательной
(индекс v от англ. vibration – колебание) и вращательной 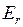 (индекс r от англ. rotation – вращение)
(индекс r от англ. rotation – вращение)
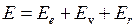 , (12.1)
, (12.1)
причем обычно 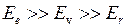 . При изменении энергии молекулы от значения
. При изменении энергии молекулы от значения 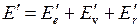 до значения
до значения 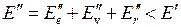 энергия испущенного фотона равна
энергия испущенного фотона равна
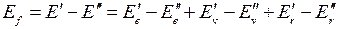 (12.2)
(12.2)
причем 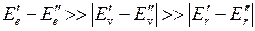 .
.
Движение электронов и ядер в молекулах можно рассматривать по отдельности из-за большой разницы в массах (приближение Борна-Оппенгеймера). Внутренние электроны атомов при образовании молекулы почти не меняют своего состояния и остаются на атомных орбиталях (АО). Вместе с атомными ядрами они образуют атомные остовы. Внешние валентные (или оптические) электроны атомов, образующих молекулу обобществляются и в соответствии с принципом Паули занимают молекулярные состояния (называемые молекулярными орбиталями, МО). Каждой электронной конфигурации − распределению валентных электронов по МО соответствует несколько молекулярных состояний (термов) с определенными энергиями 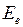 , спинами
, спинами 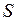 и другими квантовыми числами (аналогично атомным термам). Для двухатомных молекул зависимость электронной энергии
и другими квантовыми числами (аналогично атомным термам). Для двухатомных молекул зависимость электронной энергии 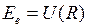 от межъядерного расстояния
от межъядерного расстояния 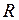 называется потенциальной функцией, а ее график – потенциальной кривой. Для каждого значения
называется потенциальной функцией, а ее график – потенциальной кривой. Для каждого значения 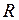 значение
значение 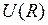 можно представить в виде суммы энергии
можно представить в виде суммы энергии 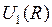 электростатического отталкивания атомных ядер (или атомных остовов) и энергии электронной подсистемы
электростатического отталкивания атомных ядер (или атомных остовов) и энергии электронной подсистемы 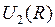 в поле ядер (остовов)
в поле ядер (остовов)
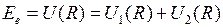 ,
, 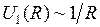 ,
, 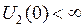 при
при 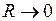 . (12.3)
. (12.3)
Схематичные изображение потенциальной кривой 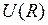 (сплошная линия) и графики функций
(сплошная линия) и графики функций 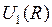 ,
, 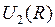 (штриховые линии 1 и 2) показаны на рис. 12.1. Асимптотическое значение
(штриховые линии 1 и 2) показаны на рис. 12.1. Асимптотическое значение 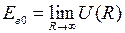 представляет собой энергию двух изолированных атомов. Точка минимума потенциальной кривой
представляет собой энергию двух изолированных атомов. Точка минимума потенциальной кривой 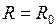 − равновесное расстояние между ядрами. Точки
− равновесное расстояние между ядрами. Точки 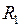 и
и 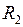 − точки поворота при радиальном движении с колебательной энергией
− точки поворота при радиальном движении с колебательной энергией 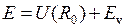 .
.
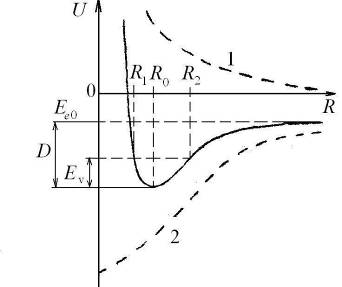
| Рис. 12.1. Схематичные графики потенциальной кривой 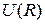 (сплошная линия), энергии взаимодействия ядер (сплошная линия), энергии взаимодействия ядер 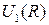 и энергии электронов в поле ядер и энергии электронов в поле ядер 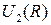 (штриховые линии 1 и 2) двухатомной молекулы (штриховые линии 1 и 2) двухатомной молекулы
|
Аналитическое выражение для потенциальной кривой 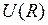 , позволяющее решить уравнение Шредингера в аналитическом виде, предложил в 1929 г. П.М.Морс
, позволяющее решить уравнение Шредингера в аналитическом виде, предложил в 1929 г. П.М.Морс
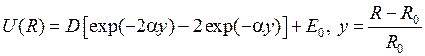 , (12.4)
, (12.4)
где 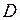 − глубина потенциальной ямы U(R). Колебательная энергия принимает дискретный ряд значений
− глубина потенциальной ямы U(R). Колебательная энергия принимает дискретный ряд значений
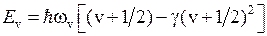 ,
, 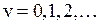 ,
, 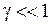 , (12.5)
, (12.5)
где 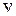 – колебательное квантовое число,
– колебательное квантовое число,
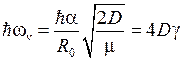 , (12.6)
, (12.6)
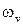 − циклическая частота малых (гармонических) колебаний,
− циклическая частота малых (гармонических) колебаний, 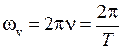 ,
,
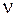 – частота и
– частота и 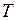 – период колебаний,
– период колебаний, 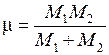 – приведенная масса двух ядер с массами
– приведенная масса двух ядер с массами 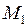 и
и 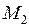 ,
, 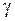 − коэффициент ангармоничности
− коэффициент ангармоничности
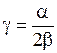 ,
, 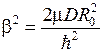 . (12.7)
. (12.7)
Малые колебания происходят вблизи минимума потенциальной кривой (рис. 12.1) где ее можно заменить параболой
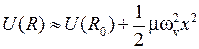 ,
, 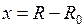 . (12.8)
. (12.8)
Поэтому для малых значений колебательного квантового числа − для низколежащих уровней, применима формула уровней линейного осциллятора
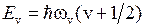 ,
, 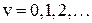 (12.9)
(12.9)
Поправка на ангармоничность колебаний постепенно уменьшает расстояния между уровнями
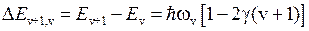 . (12.10)
. (12.10)
Максимальное значение квантового числа 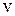 определяется из условия
определяется из условия 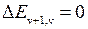
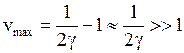 . (12.11)
. (12.11)
Максимальная энергия колебательного движения
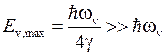 . (12.12)
. (12.12)
Энергия диссоциации двухатомной молекулы
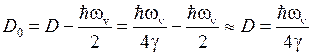 . (12.13)
. (12.13)
Значения параметров 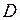 ,
, 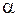 ,
, 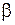 ,
, 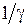 для трех двухатомных молекул: водорода (см. работу 11), гидроксила (см. работу 13) и йода приведены в табл. 12.1.
для трех двухатомных молекул: водорода (см. работу 11), гидроксила (см. работу 13) и йода приведены в табл. 12.1.
Таблица 12.1.
| Молекула
| 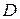 , эВ , эВ
| 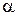
| 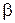
| 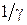
|
| H2
| 4,48
| 1,44
| 25,09
| 34,9
|
| OH
| 4,33
| 2,29
| 42,9
| 43,3
|
| I2
| 1,56
| 4,95
| 579,5
| 234
|
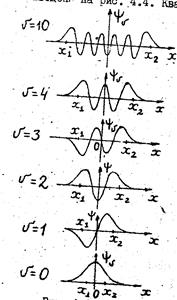
Графики колебательных волновых функций 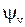 в гармоническом приближении (12.8) показаны на рис. 12.2. Квадрат модуля волновой функции
в гармоническом приближении (12.8) показаны на рис. 12.2. Квадрат модуля волновой функции 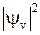 есть плотность вероятности нахождения ядер на расстоянии
есть плотность вероятности нахождения ядер на расстоянии 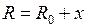 друг от друга. В основном состоянии (для
друг от друга. В основном состоянии (для 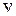 =0) плотность вероятности
=0) плотность вероятности 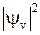 максимальна при
максимальна при 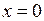 ,
, 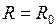 .
.
Качественное представление о движении ядер (атомных остовов) дают классические траектории, показанные на рис. 11.3 и 13.2. При колебании ядер (рис. 11.3) с энергией 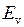 согласно классической механике расстояние
согласно классической механике расстояние 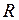 между ними меняется в пределах от
между ними меняется в пределах от 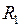 до
до 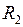 (см. рис. 12.1). Вблизи дна потенциальной ямы при
(см. рис. 12.1). Вблизи дна потенциальной ямы при  потенциальная кривая близка к параболе и колебания ядер являются почти гармоническими. С ростом энергии
потенциальная кривая близка к параболе и колебания ядер являются почти гармоническими. С ростом энергии 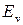 колебания становятся ангармоническими, а среднее межъядерное расстояние
колебания становятся ангармоническими, а среднее межъядерное расстояние 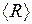 смещается от
смещается от 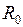 вправо. Вращение ядер вокруг оси ОВ, перпендикулярной оси молекулы ОА показано на рис. 13.2а. Сочетание вращения и колебаний показано на рис. 13.2б.
вправо. Вращение ядер вокруг оси ОВ, перпендикулярной оси молекулы ОА показано на рис. 13.2а. Сочетание вращения и колебаний показано на рис. 13.2б.
| Рис. 12.2. Колебательные волновые функции основного и возбужденных состояний линейного осциллятора
| 
|
Качественную картину движения валентного электрона в поле ядер (остовов) дают классические траектории на рис. 11.1. Траектория на рис. 11.1а соответствует положительной проекции 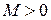 момента импульса электрона на ось молекулы ОА, а траектория на рис. 11.1б – нулевой проекции
момента импульса электрона на ось молекулы ОА, а траектория на рис. 11.1б – нулевой проекции 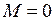 . Вращению в направлении, противоположном показанному на рис. 11.1а соответствует отрицательная проекция момента
. Вращению в направлении, противоположном показанному на рис. 11.1а соответствует отрицательная проекция момента 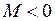 . Поле двух ядер (остовов) имеет осевую симметрию относительно оси ОА, поэтому проекция момента импульса на ось молекулы сохраняется неизменной
. Поле двух ядер (остовов) имеет осевую симметрию относительно оси ОА, поэтому проекция момента импульса на ось молекулы сохраняется неизменной 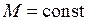 .
.
При квантовом описании проекция момента импульса электрона на ось молекулы квантуется
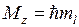 ,
, 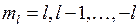 , (12.14)
, (12.14)
где 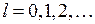 – орбитальное квантовое число. Состояния с квантовыми числами
– орбитальное квантовое число. Состояния с квантовыми числами
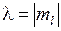 ,
, 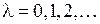 , (12.15)
, (12.15)
обозначаются греческими буквами  ,
, 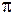 ,
, 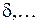 по аналогии с латинскими буквами s, p, d,…, которыми обозначаются состояния с
по аналогии с латинскими буквами s, p, d,…, которыми обозначаются состояния с 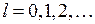 в атомах. Соответствующие волновые функции называют
в атомах. Соответствующие волновые функции называют  -орбиталями,
-орбиталями, 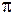 -орбиталями и так далее. По принципу Паули на
-орбиталями и так далее. По принципу Паули на  -орбиталях может находиться не более двух электронов (с противоположными спинами), на остальных орбиталях – не более четырех, поскольку для каждого значения проекции спина на ось молекулы (
-орбиталях может находиться не более двух электронов (с противоположными спинами), на остальных орбиталях – не более четырех, поскольку для каждого значения проекции спина на ось молекулы ( 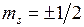 ) возможны два состояния, отличающиеся знаком проекции момента на ось, или (в классической картине) направлением вращения электрона вокруг оси молекулы. Молекулярные термы с проекцией полного момента на ось молекулы
) возможны два состояния, отличающиеся знаком проекции момента на ось, или (в классической картине) направлением вращения электрона вокруг оси молекулы. Молекулярные термы с проекцией полного момента на ось молекулы
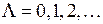 (12.16)
(12.16)
Обозначаются заглавными греческими буквами 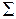 ,
, 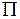 ,
, 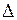 ,…. Полный спин
,…. Полный спин 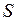 молекулы принято приводить в форме мультиплетности
молекулы принято приводить в форме мультиплетности 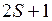 , которая указывается вверху слева от символа, например
, которая указывается вверху слева от символа, например 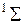 ,
, 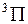 ,
, 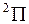 , так же как у атомных термов, например
, так же как у атомных термов, например 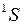 ,
, 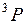 ,
, 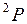 . Полный электронный момент молекулы Квантовое число
. Полный электронный момент молекулы Квантовое число 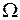 , равное модулю проекции суммарного электронного момента импульса на ось z:
, равное модулю проекции суммарного электронного момента импульса на ось z: 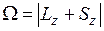 находится по правилу сложения моментов
находится по правилу сложения моментов 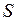 и
и 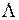 . Величина
. Величина 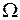 указывается в правом нижнем углу символа состояния, например,
указывается в правом нижнем углу символа состояния, например, 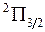 ,
, 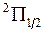 ,
, 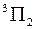 ,
, 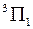 ,
, 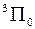 .
.





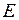 может быть приближенно представлена суммой трех энергий: электронной
может быть приближенно представлена суммой трех энергий: электронной 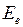 , колебательной
, колебательной 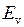 (индекс v от англ. vibration – колебание) и вращательной
(индекс v от англ. vibration – колебание) и вращательной 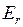 (индекс r от англ. rotation – вращение)
(индекс r от англ. rotation – вращение)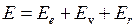 , (12.1)
, (12.1)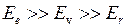 . При изменении энергии молекулы от значения
. При изменении энергии молекулы от значения 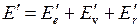 до значения
до значения 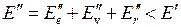 энергия испущенного фотона равна
энергия испущенного фотона равна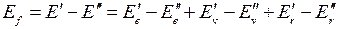 (12.2)
(12.2)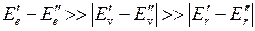 .
.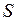 и другими квантовыми числами (аналогично атомным термам). Для двухатомных молекул зависимость электронной энергии
и другими квантовыми числами (аналогично атомным термам). Для двухатомных молекул зависимость электронной энергии 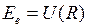 от межъядерного расстояния
от межъядерного расстояния 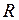 называется потенциальной функцией, а ее график – потенциальной кривой. Для каждого значения
называется потенциальной функцией, а ее график – потенциальной кривой. Для каждого значения 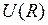 можно представить в виде суммы энергии
можно представить в виде суммы энергии 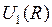 электростатического отталкивания атомных ядер (или атомных остовов) и энергии электронной подсистемы
электростатического отталкивания атомных ядер (или атомных остовов) и энергии электронной подсистемы 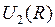 в поле ядер (остовов)
в поле ядер (остовов)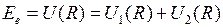 ,
, 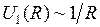 ,
, 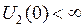 при
при 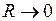 . (12.3)
. (12.3)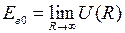 представляет собой энергию двух изолированных атомов. Точка минимума потенциальной кривой
представляет собой энергию двух изолированных атомов. Точка минимума потенциальной кривой 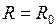 − равновесное расстояние между ядрами. Точки
− равновесное расстояние между ядрами. Точки 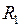 и
и 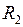 − точки поворота при радиальном движении с колебательной энергией
− точки поворота при радиальном движении с колебательной энергией 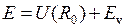 .
.
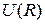 (сплошная линия), энергии взаимодействия ядер
(сплошная линия), энергии взаимодействия ядер 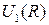 и энергии электронов в поле ядер
и энергии электронов в поле ядер 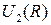 (штриховые линии 1 и 2) двухатомной молекулы
(штриховые линии 1 и 2) двухатомной молекулы
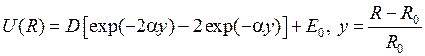 , (12.4)
, (12.4)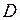 − глубина потенциальной ямы U(R). Колебательная энергия принимает дискретный ряд значений
− глубина потенциальной ямы U(R). Колебательная энергия принимает дискретный ряд значений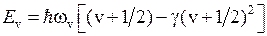 ,
, 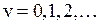 ,
, 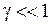 , (12.5)
, (12.5)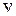 – колебательное квантовое число,
– колебательное квантовое число,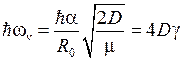 , (12.6)
, (12.6)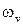 − циклическая частота малых (гармонических) колебаний,
− циклическая частота малых (гармонических) колебаний, 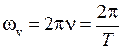 ,
,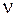 – частота и
– частота и 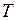 – период колебаний,
– период колебаний, 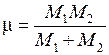 – приведенная масса двух ядер с массами
– приведенная масса двух ядер с массами 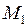 и
и 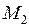 ,
, 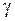 − коэффициент ангармоничности
− коэффициент ангармоничности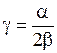 ,
, 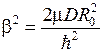 . (12.7)
. (12.7) 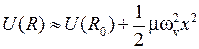 ,
, 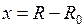 . (12.8)
. (12.8)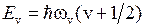 ,
, 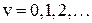 (12.9)
(12.9)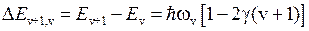 . (12.10)
. (12.10)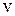 определяется из условия
определяется из условия 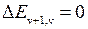
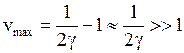 . (12.11)
. (12.11)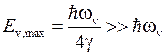 . (12.12)
. (12.12)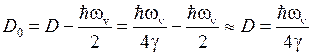 . (12.13)
. (12.13)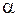 ,
, 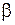 ,
, 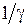 для трех двухатомных молекул: водорода (см. работу 11), гидроксила (см. работу 13) и йода приведены в табл. 12.1.
для трех двухатомных молекул: водорода (см. работу 11), гидроксила (см. работу 13) и йода приведены в табл. 12.1.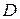 , эВ
, эВ
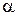
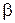
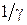
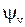 в гармоническом приближении (12.8) показаны на рис. 12.2. Квадрат модуля волновой функции
в гармоническом приближении (12.8) показаны на рис. 12.2. Квадрат модуля волновой функции 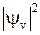 есть плотность вероятности нахождения ядер на расстоянии
есть плотность вероятности нахождения ядер на расстоянии 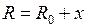 друг от друга. В основном состоянии (для
друг от друга. В основном состоянии (для 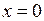 ,
,  потенциальная кривая близка к параболе и колебания ядер являются почти гармоническими. С ростом энергии
потенциальная кривая близка к параболе и колебания ядер являются почти гармоническими. С ростом энергии 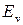 колебания становятся ангармоническими, а среднее межъядерное расстояние
колебания становятся ангармоническими, а среднее межъядерное расстояние 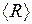 смещается от
смещается от 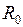 вправо. Вращение ядер вокруг оси ОВ, перпендикулярной оси молекулы ОА показано на рис. 13.2а. Сочетание вращения и колебаний показано на рис. 13.2б.
вправо. Вращение ядер вокруг оси ОВ, перпендикулярной оси молекулы ОА показано на рис. 13.2а. Сочетание вращения и колебаний показано на рис. 13.2б.
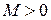 момента импульса электрона на ось молекулы ОА, а траектория на рис. 11.1б – нулевой проекции
момента импульса электрона на ось молекулы ОА, а траектория на рис. 11.1б – нулевой проекции 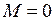 . Вращению в направлении, противоположном показанному на рис. 11.1а соответствует отрицательная проекция момента
. Вращению в направлении, противоположном показанному на рис. 11.1а соответствует отрицательная проекция момента 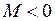 . Поле двух ядер (остовов) имеет осевую симметрию относительно оси ОА, поэтому проекция момента импульса на ось молекулы сохраняется неизменной
. Поле двух ядер (остовов) имеет осевую симметрию относительно оси ОА, поэтому проекция момента импульса на ось молекулы сохраняется неизменной 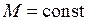 .
.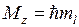 ,
, 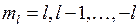 , (12.14)
, (12.14)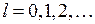 – орбитальное квантовое число. Состояния с квантовыми числами
– орбитальное квантовое число. Состояния с квантовыми числами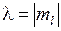 ,
, 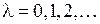 , (12.15)
, (12.15) ,
, 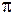 ,
, 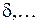 по аналогии с латинскими буквами s, p, d,…, которыми обозначаются состояния с
по аналогии с латинскими буквами s, p, d,…, которыми обозначаются состояния с 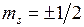 ) возможны два состояния, отличающиеся знаком проекции момента на ось, или (в классической картине) направлением вращения электрона вокруг оси молекулы. Молекулярные термы с проекцией полного момента на ось молекулы
) возможны два состояния, отличающиеся знаком проекции момента на ось, или (в классической картине) направлением вращения электрона вокруг оси молекулы. Молекулярные термы с проекцией полного момента на ось молекулы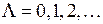 (12.16)
(12.16)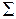 ,
, 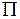 ,
, 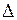 ,…. Полный спин
,…. Полный спин 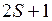 , которая указывается вверху слева от символа, например
, которая указывается вверху слева от символа, например 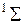 ,
, 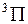 ,
, 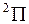 , так же как у атомных термов, например
, так же как у атомных термов, например 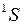 ,
, 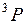 ,
, 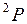 . Полный электронный момент молекулы Квантовое число
. Полный электронный момент молекулы Квантовое число 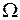 , равное модулю проекции суммарного электронного момента импульса на ось z:
, равное модулю проекции суммарного электронного момента импульса на ось z: 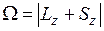 находится по правилу сложения моментов
находится по правилу сложения моментов 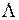 . Величина
. Величина 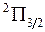 ,
, 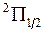 ,
, 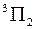 ,
, 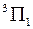 ,
, 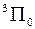 .
.


