Энергия молекулы 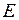 может быть приближенно представлена суммой трех энергий: электронной
может быть приближенно представлена суммой трех энергий: электронной 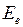 , колебательной
, колебательной 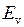 (индекс v от англ. vibration – колебание) и вращательной
(индекс v от англ. vibration – колебание) и вращательной 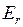 (индекс r от англ. rotation – вращение),
(индекс r от англ. rotation – вращение),
[2-7,19-21]
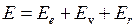 , (11.1)
, (11.1)
причем обычно 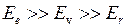 . В данной работе рассматриваются только электронная и колебательная энергия - основные слагаемые в формуле 11.1), изучению вращательной энергии посвящена работа 4.6.
. В данной работе рассматриваются только электронная и колебательная энергия - основные слагаемые в формуле 11.1), изучению вращательной энергии посвящена работа 4.6.
Движение электронов и ядер в молекулах можно рассматривать по отдельности из-за большой разницы в массах. Оба электрона атомов водорода, образующих молекулу Н2, обобществляются и могут двигаться в пределах всей молекулы. Качественную картину движения одного из электронов в поле двух ядер водорода (протонов) дают классические траектории на рис. 11.1.
| а
б
| 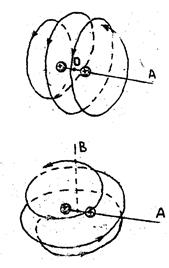
| Рис. 11.1. Качественная картина классических траекторий электронов с разными проекциями момента импульса на ось ОА молекулы Н2
|
Верхняя траектория на рис. 11.1 соответствует положительной проекции 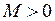 момента импульса электрона на ось молекулы ОА, вращению в противоположном направлении соответствует отрицательная проекция момента
момента импульса электрона на ось молекулы ОА, вращению в противоположном направлении соответствует отрицательная проекция момента 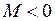 . Нижняя траектория соответствует нулевой проекции
. Нижняя траектория соответствует нулевой проекции 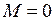 .
.
Поле двух ядер (остовов) имеет осевую симметрию (относительно оси ОА), поэтому проекция момента импульса на ось двухатомной молекулы сохраняется неизменной 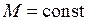 . При квантовом описании проекция момента импульса электрона на ось молекулы квантуется
. При квантовом описании проекция момента импульса электрона на ось молекулы квантуется
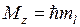 ,
, 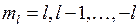 , (11.2)
, (11.2)
где 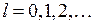 − орбитальное квантовое число. Решение уравнения Шредингера для энергий и волновых функций электрона в поле двух ядер приводит к молекулярным состояниям, называемым молекулярными орбиталями (МО). Состояния с квантовыми числами
− орбитальное квантовое число. Решение уравнения Шредингера для энергий и волновых функций электрона в поле двух ядер приводит к молекулярным состояниям, называемым молекулярными орбиталями (МО). Состояния с квантовыми числами
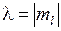 ,
, 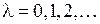 , (11.3)
, (11.3)
обозначаются греческими буквами  ,
, 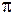 ,
, 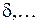 по аналогии с латинскими буквами s,p,d,…, для обозначений состояний с
по аналогии с латинскими буквами s,p,d,…, для обозначений состояний с 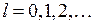 в атомах. Соответствующие волновые функции называют
в атомах. Соответствующие волновые функции называют  -орбиталями,
-орбиталями,
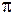 -орбиталями и так далее. По принципу Паули на
-орбиталями и так далее. По принципу Паули на  -орбиталях может находиться не более двух электронов с противоположными спинами. На остальных орбиталях число электронов не более четырех, поскольку для каждого значения проекции спина на ось молекулы (
-орбиталях может находиться не более двух электронов с противоположными спинами. На остальных орбиталях число электронов не более четырех, поскольку для каждого значения проекции спина на ось молекулы ( 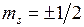 ) возможны два состояния, отличающиеся знаком проекции момента на ось (
) возможны два состояния, отличающиеся знаком проекции момента на ось ( 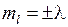 ), в качественной классической картине этому соответствует два направления вращения электрона вокруг оси молекулы. В данной работе рассматриваются только такие состояния молекулы водорода, у которых оба электрона находятся в
), в качественной классической картине этому соответствует два направления вращения электрона вокруг оси молекулы. В данной работе рассматриваются только такие состояния молекулы водорода, у которых оба электрона находятся в  -состояниях с
-состояниях с 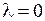 , а модуль проекции полного орбитального момента электронов на ось молекулы
, а модуль проекции полного орбитального момента электронов на ось молекулы 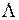 равен нулю
равен нулю 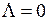 . Такие состояния (термы) обозначаются заглавной греческой буквой
. Такие состояния (термы) обозначаются заглавной греческой буквой 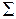 , см. табл. П9.3 в Прил. 9. Сложение спинов двух электронов по правилу сложения моментов (см. работу 10) дает два возможных значения полного спина
, см. табл. П9.3 в Прил. 9. Сложение спинов двух электронов по правилу сложения моментов (см. работу 10) дает два возможных значения полного спина 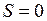 и
и 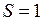 . В первом случае состояния называются синглетными, во втором – триплетными. Полный спин
. В первом случае состояния называются синглетными, во втором – триплетными. Полный спин 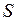 молекулы, как и у атома, принято приводить в форме мультиплетности
молекулы, как и у атома, принято приводить в форме мультиплетности 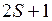 , которая указывается вверху слева от символа терма, например
, которая указывается вверху слева от символа терма, например 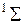 ,
, 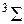 , так же как у атомных термов, например
, так же как у атомных термов, например 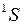 ,
, 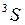 , см. работу 10 и рис. 10.4.
, см. работу 10 и рис. 10.4.
Для двухатомных молекул зависимость электронной энергии 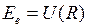 от межъядерного расстояния
от межъядерного расстояния 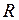 называется потенциальной функцией, а ее график – потенциальной кривой. Величину
называется потенциальной функцией, а ее график – потенциальной кривой. Величину 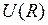 для молекулы водорода можно представить в виде суммы энергии
для молекулы водорода можно представить в виде суммы энергии 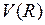 электростатического отталкивания атомных ядер (протонов) и энергии электронной подсистемы
электростатического отталкивания атомных ядер (протонов) и энергии электронной подсистемы 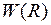 в поле ядер
в поле ядер
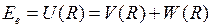 ,
, 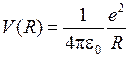 , (11.4)
, (11.4)
где 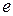 - элементарный заряд. Схематичные изображения некоторых потенциальных кривых
- элементарный заряд. Схематичные изображения некоторых потенциальных кривых  молекулы водорода показаны на рис. 11.2.
молекулы водорода показаны на рис. 11.2.
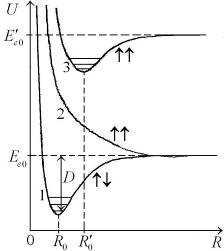
| Рис. 11.2. Схематические графики потенциальных кривых 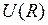 синглетного ( синглетного ( 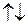 ) и двух триплетных ( ) и двух триплетных ( 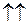 ) состояний молекулы водорода Н2. Горизонтальными отрезками обозначены низколежащие колебательные состояния ) состояний молекулы водорода Н2. Горизонтальными отрезками обозначены низколежащие колебательные состояния
|
Кривая для синглетного состояния с полным спином двух электронов  на рис. 11.2 обозначена двумя противоположно направленными стрелками
на рис. 11.2 обозначена двумя противоположно направленными стрелками 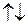 , изображающими взаимную ориентацию спинов электронов. Две кривые для триплетных состояний с полным спином
, изображающими взаимную ориентацию спинов электронов. Две кривые для триплетных состояний с полным спином 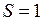 обозначены параллельными стрелками
обозначены параллельными стрелками 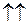 . Кривая 1 отвечает минимальной электронной энергии
. Кривая 1 отвечает минимальной электронной энергии 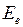 - основному состоянию молекулы водорода с равновесным межъядерным расстоянием
- основному состоянию молекулы водорода с равновесным межъядерным расстоянием 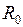 =0.074 нм. Глубина потенциальной ямы синглетного состояния
=0.074 нм. Глубина потенциальной ямы синглетного состояния 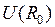 приблизительно равна энергии диссоциации – распада молекулы на атомы
приблизительно равна энергии диссоциации – распада молекулы на атомы 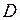 =4.48 эВ (точнее см. формулу (11.11)). Асимптотическое значение электронной энергии
=4.48 эВ (точнее см. формулу (11.11)). Асимптотическое значение электронной энергии 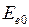 при
при 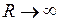 равно сумме энергий двух атомов водорода с электронами в основном состоянии с главным квантовым числом
равно сумме энергий двух атомов водорода с электронами в основном состоянии с главным квантовым числом 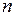 =1 (в состоянии 1s). Кривая 2 отвечает триплетному неустойчивому состоянию, переходящему при
=1 (в состоянии 1s). Кривая 2 отвечает триплетному неустойчивому состоянию, переходящему при 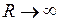 в два атома водорода в основных состояниях с параллельными спинами электронов*. Кривая 3 соответствует возбужденному устойчивому триплетному состоянию с равновесным межъядерным расстоянием
в два атома водорода в основных состояниях с параллельными спинами электронов*. Кривая 3 соответствует возбужденному устойчивому триплетному состоянию с равновесным межъядерным расстоянием 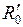 =0,1 нм. Асимптотическое значение электронной энергии
=0,1 нм. Асимптотическое значение электронной энергии 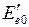 при
при 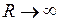 равно сумме энергий двух атомов водорода, у одного из которых электрон находится в основном состоянии с главным квантовым числом
равно сумме энергий двух атомов водорода, у одного из которых электрон находится в основном состоянии с главным квантовым числом 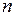 =1 (в состоянии 1s), а у другого – в возбужденном состоянии с главным квантовым числом
=1 (в состоянии 1s), а у другого – в возбужденном состоянии с главным квантовым числом 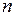 =2 (в данном случае в состоянии 2s).
=2 (в данном случае в состоянии 2s).
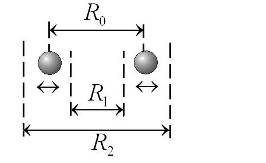
Качественное представление о движении ядер (атомных остовов) дает рис. 11.3. При колебании ядер с энергией 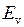 расстояние
расстояние 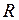 между ними меняется в пределах от
между ними меняется в пределах от 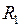 до
до 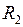 , где
, где 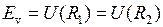 (рис. 11.3).
(рис. 11.3).
| Рис. 11.3. Качественная картина колебаний атомных ядер в двухатомной молекуле
| 
|
Вблизи дна потенциальной ямы при  потенциальная кривая близка к параболе
потенциальная кривая близка к параболе
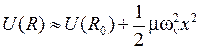 ,
, 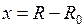 , (11.5)
, (11.5)
и колебания ядер являются почти гармоническими с циклической частотой 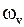 ,
,
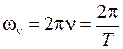 , (11.6)
, (11.6)
частотой 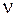 и периодом
и периодом 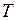 . Приведенная масса молекулы с массами атомов
. Приведенная масса молекулы с массами атомов 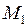 и
и 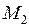
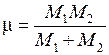 , (11.7)
, (11.7)
для молекулы водорода равна
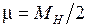 , (11.8)
, (11.8)
где 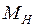 – масса ядра атома водорода. С ростом энергии
– масса ядра атома водорода. С ростом энергии 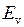 колебания становятся ангармоническими, а среднее межъядерное расстояние
колебания становятся ангармоническими, а среднее межъядерное расстояние 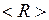 смещается от
смещается от 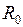 вправо.
вправо.
Колебательная энергия квантового осциллятора принимает дискретный ряд значений. Для низколежащих уровней применима формула уровней линейного осциллятора
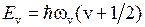 ,
, 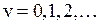 , (11.9)
, (11.9)
где 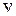 – колебательное квантовое число. Колебательные уровни
– колебательное квантовое число. Колебательные уровни 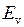 и
и 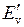 для двух электронных энергий
для двух электронных энергий 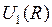 и
и 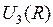 показаны на рис. 11.2. Минимальная колебательная энергия (называемая также энергией нулевых колебаний) равна
показаны на рис. 11.2. Минимальная колебательная энергия (называемая также энергией нулевых колебаний) равна
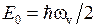 , (11.10)
, (11.10)
поэтому точное выражение для энергии диссоциации
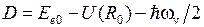 . (11.11)
. (11.11)
Более точная формула для энергий колебательных уровней имеет вид
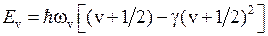 ,
, 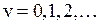 , (11.12)
, (11.12)
поэтому интервалы между уровнями постепенно уменьшаются
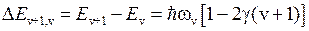 , (11.13)
, (11.13)
до нуля при максимальном значении колебательного квантового числа
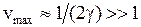 , (11.14)
, (11.14)
Параметр 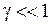 называется коэффициентом ангармоничности.
называется коэффициентом ангармоничности.
2. Строение, электронные состояния и спектр молекулы водорода Н2.
В основном состоянии молекулы водорода оба электрона занимают молекулярное состояние (молекулярную орбиталь, МО), обозначаемую 1s  . Символ 1s перед символом
. Символ 1s перед символом 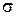 указывает, что при сближении ядер,
указывает, что при сближении ядер, 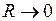 и гипотетическом образовании из них “объединенного ядра” с зарядом
и гипотетическом образовании из них “объединенного ядра” с зарядом 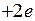 эта молекулярная орбиталь (МО) непрерывно перешла бы в основное состояние электрона в поле “объединенного ядра” – в атомную орбиталь (АО) 1s. Из-за малости межъядерного расстояния
эта молекулярная орбиталь (МО) непрерывно перешла бы в основное состояние электрона в поле “объединенного ядра” – в атомную орбиталь (АО) 1s. Из-за малости межъядерного расстояния 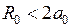 , где
, где 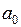 – боровский радиус,
– боровский радиус, 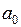 =0,0529 нм, между АО 1s “объединенного ядра” и МО 1s
=0,0529 нм, между АО 1s “объединенного ядра” и МО 1s  сохраняется определенное сходство, заметное при изображении двух поперечных сечений распределения электронной плотности вероятности
сохраняется определенное сходство, заметное при изображении двух поперечных сечений распределения электронной плотности вероятности 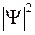 на рис. 11.4 (
на рис. 11.4 ( 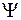 – волновая функция электрона). Одно из поперечных сечений содержит межъядерную ось (рис. 11.4а), другое перпендикулярно ей (рис. 11.4б).
– волновая функция электрона). Одно из поперечных сечений содержит межъядерную ось (рис. 11.4а), другое перпендикулярно ей (рис. 11.4б).
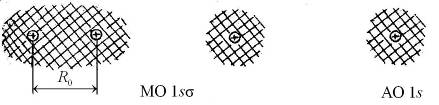
а б в
Рис. 11.4. Схематичное изображение двух поперечных сечений (а и б) распределения электронной плотности вероятности 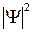 (
( 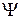 − волновая функция электрона) для МО 1s
− волновая функция электрона) для МО 1s 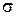 молекулы Н2 и АО 1s “объединенного ядра” (в)
молекулы Н2 и АО 1s “объединенного ядра” (в)
На рис. 11.4 штриховкой показаны области, в которых не мала плотность вероятности 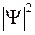 нахождения электрона в разных точках поперечных сечений для основного молекулярного состояния 1s
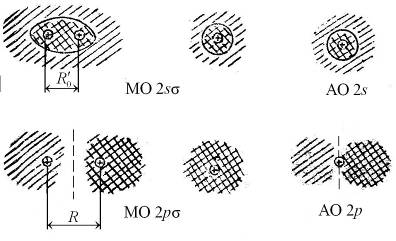
нахождения электрона в разных точках поперечных сечений для основного молекулярного состояния 1s  и основного атомного состояния 1s. Примерами низколежащих возбужденных молекулярных состояний являются МО 2s
и основного атомного состояния 1s. Примерами низколежащих возбужденных молекулярных состояний являются МО 2s  и 2р
и 2р  , схематично показанные на рис. 11.5. При
, схематично показанные на рис. 11.5. При 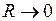 и образовании “объединенного ядра” с зарядом
и образовании “объединенного ядра” с зарядом 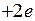 эти молекулярные орбитали непрерывно переходят в состояния электрона в поле “объединенного ядра” – в атомные орбитали (АО) 2s и 2p.
эти молекулярные орбитали непрерывно переходят в состояния электрона в поле “объединенного ядра” – в атомные орбитали (АО) 2s и 2p.
Рис. 11.5. Схематичное изображение двух поперечных сечений (а и б) распределения электронной плотности вероятности 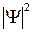 ( ( 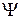 − волновая функция электрона) для МО 2s − волновая функция электрона) для МО 2s 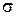 , 2р , 2р 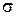 молекулы Н2 и АО 2s и 2p для “объединенного ядра” (в) молекулы Н2 и АО 2s и 2p для “объединенного ядра” (в)
|  а б в
а б в
|
Для МО 2s  и 2р
и 2р  на рис. 11.5 изображены два поперечных сечения, такие же, как на рис. 11.4. Указаны линии пересечения с плоскостями сечений узловых поверхностей волновых функций, на которых
на рис. 11.5 изображены два поперечных сечения, такие же, как на рис. 11.4. Указаны линии пересечения с плоскостями сечений узловых поверхностей волновых функций, на которых 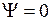 . Знак волновой функции (– или +) указан одинарной или двойной штриховкой.
. Знак волновой функции (– или +) указан одинарной или двойной штриховкой.
Возбужденные состояния молекулы Н2, с потенциальными кривыми 2,3 на рис. 11.2, образуются при переходе с переворотом спина одного из электронов с МО 1s  на вышележащие МО 2s
на вышележащие МО 2s  , 2р
, 2р  при неупругих столкновениях с электронами во время электрического разряда. Кривой 2 соответствует электронная конфигурация 1s
при неупругих столкновениях с электронами во время электрического разряда. Кривой 2 соответствует электронная конфигурация 1s  2р
2р  (обозначается
(обозначается 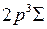 ), кривой 3 – конфигурация 1s
), кривой 3 – конфигурация 1s  2s
2s  (обозначается
(обозначается 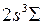 ). Переход молекулы из вышележащего устойчивого возбужденного состояния
). Переход молекулы из вышележащего устойчивого возбужденного состояния 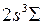 в неустойчивое нижележащее возбужденное состояние
в неустойчивое нижележащее возбужденное состояние 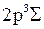 с испусканием света разрешен правилами отбора. Именно таким переходам обусловлен, в основном, сплошной спектр излучения молекулы Н2. Точные потенциальные кривые
с испусканием света разрешен правилами отбора. Именно таким переходам обусловлен, в основном, сплошной спектр излучения молекулы Н2. Точные потенциальные кривые 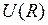 состояний (термов)
состояний (термов) 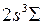 ,
, 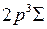 показаны на рис. 11.6а.
показаны на рис. 11.6а.
Горизонтальными отрезками 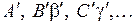 , так же как на рис. 11.2 показаны пять колебательных уровней
, так же как на рис. 11.2 показаны пять колебательных уровней  терма
терма 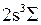 с квантовыми числами
с квантовыми числами 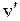 =0,1,2,3,4, Для их энергий применима формула (11.9) линейного осциллятора. Концы отрезков
=0,1,2,3,4, Для их энергий применима формула (11.9) линейного осциллятора. Концы отрезков 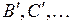 и
и 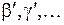 – это точки поворота, ограничивающие область, доступную для движения ядер водорода по законам классической механики. Справа вверху показана волновая функция
– это точки поворота, ограничивающие область, доступную для движения ядер водорода по законам классической механики. Справа вверху показана волновая функция 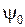 основного колебательного состояния, она быстро стремится к нулю при удалении от точек поворота в глубь классически недоступной области.
основного колебательного состояния, она быстро стремится к нулю при удалении от точек поворота в глубь классически недоступной области.
а б
Рис. 11.6. Потенциальные кривые  возбужденных состояний (термов)
возбужденных состояний (термов) 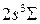 ,
, 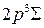 молекулы Н2 [15, рис. 9.6], [23] (а) и волновые функции основного состояния терма
молекулы Н2 [15, рис. 9.6], [23] (а) и волновые функции основного состояния терма 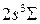 и состояния терма
и состояния терма 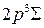 с энергией, соответствующей точке
с энергией, соответствующей точке 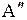 потенциальной кривой [12] (б).
потенциальной кривой [12] (б).
Энергия образующегося терма 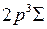 может принимать любые значения от 0 до энергии, примерно равной соответствующей точке
может принимать любые значения от 0 до энергии, примерно равной соответствующей точке 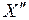 . Для энергии терма
. Для энергии терма 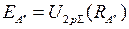 точка
точка 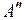 является точкой поворота
является точкой поворота 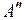 движения ядер водорода. Справа внизу показана волновая функция
движения ядер водорода. Справа внизу показана волновая функция 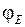 *.
*.
Вертикальные штриховые линии 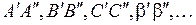 указывают некоторые наиболее вероятные электронные переходы, происходящие настолько быстро, что межъядерное расстояние не успевает измениться (в соответствии с принципом Франка-Кондона). Длины этих отрезков (в эВ) равны энергиям
указывают некоторые наиболее вероятные электронные переходы, происходящие настолько быстро, что межъядерное расстояние не успевает измениться (в соответствии с принципом Франка-Кондона). Длины этих отрезков (в эВ) равны энергиям 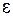 излучаемых при переходах фотонов. Поскольку энергия фотонов при таких переходах принимает непрерывный ряд значений из некоторого интервала, спектр излучения будет сплошным в некотором диапазоне длин волн. Соответствующие переходам межъядерные расстояния
излучаемых при переходах фотонов. Поскольку энергия фотонов при таких переходах принимает непрерывный ряд значений из некоторого интервала, спектр излучения будет сплошным в некотором диапазоне длин волн. Соответствующие переходам межъядерные расстояния 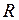 лежат преимущественно в пределах классически доступных областей колебательных состояний (
лежат преимущественно в пределах классически доступных областей колебательных состояний ( 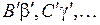 ), заселенных с большой вероятностью согласно распределению Больцмана
), заселенных с большой вероятностью согласно распределению Больцмана
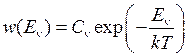 , (11.15)
, (11.15)
где 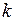 − постоянная Больцмана,
− постоянная Больцмана, 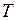 – абсолютная температура газа при электрическом разряде. Вероятность перехода из колебательного состояния в диссоциирующее (распадающееся) состояние с волновой функцией
– абсолютная температура газа при электрическом разряде. Вероятность перехода из колебательного состояния в диссоциирующее (распадающееся) состояние с волновой функцией 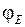 пропорциональна квадрату модуля интеграла перекрытия волновых функций
пропорциональна квадрату модуля интеграла перекрытия волновых функций
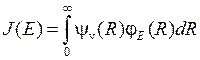 , (11.16)
, (11.16)
Типичные графики волновых функций 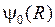 ,
, 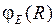 для перехода
для перехода 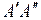 показаны на рис. 11.6б. В соответствии с формулой (11.16) наиболее вероятны переходы в такие состояния
показаны на рис. 11.6б. В соответствии с формулой (11.16) наиболее вероятны переходы в такие состояния 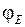 , у которых максимум
, у которых максимум 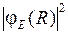 (лежащий чуть правее точки поворота) находится примерно на том же межъядерном расстоянии
(лежащий чуть правее точки поворота) находится примерно на том же межъядерном расстоянии 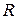 , что и максимум
, что и максимум 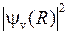 (см. рис.11.6).
(см. рис.11.6).
Примеры сплошного спектра двухатомных молекул и его применение
Сплошной спектр излучения, аналогичный водородному, имеется и у некоторых других молекул. При электрическом разряде в парах ртути может образовываться молекула Hg2, которая испускает сплошной спектр в диапазоне 330-254 нм и вблизи 480 нм. В первом случае эта молекула распадается на атомы ртути в состояниях 61S и 63Р0,1,2 и во втором – на атомы в состояниях 61S и 61Р1 (см. работу 10 и рис. 10.4).
Еще одним примером сплошного спектра является излучение неустойчивых молекул инертных газов Xe2, Ar2, Kr2, называемые эксимерами, и молекул типа XeF, KrF, называемые эксиплексами [7, с. 132]. Типичная молекула Xe2 образуется из двух атомов ксенона – одного в основном состоянии, другого в возбужденном (см. работу 8). Потенциальная кривая такой системы сходна с верхней кривой на рис. 11.6а. Потенциальная кривая для сближения двух атомов Хе в основном состоянии сходна с нижней кривой на рис. 11.6а. Переходы, аналогичные вертикальным отрезкам  на рис. 11.6а приводят к излучению сплошного спектра и диссоциации молекулы Xe2. На использовании таких переходов основано действие эксимерного Xe2-лазера и других аналогичных лазеров. Возбуждение атомов Хе в них производится импульсным электронным пучком. При давлении не ниже 1 МПа (10 атм) достаточно велика вероятность столкновения двух атомов ксенона, один из которых находится в возбужденном состоянии. При участии в столкновении третьего атома или стенки сосуда могут образовываться эксимеры Xe2. Вероятность нахождения атомов Хе на равновесном расстоянии
на рис. 11.6а приводят к излучению сплошного спектра и диссоциации молекулы Xe2. На использовании таких переходов основано действие эксимерного Xe2-лазера и других аналогичных лазеров. Возбуждение атомов Хе в них производится импульсным электронным пучком. При давлении не ниже 1 МПа (10 атм) достаточно велика вероятность столкновения двух атомов ксенона, один из которых находится в возбужденном состоянии. При участии в столкновении третьего атома или стенки сосуда могут образовываться эксимеры Xe2. Вероятность нахождения атомов Хе на равновесном расстоянии 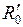 в устойчивом возбужденном состоянии гораздо выше, чем в неустойчивом основном состоянии. Это создает инверсию заселенности уровней, и, если газ находится в оптическом резонаторе, можно получить лазерную генерацию. Энергия фотонов составляет при этом около 7,1 эВ, для переходов типа
в устойчивом возбужденном состоянии гораздо выше, чем в неустойчивом основном состоянии. Это создает инверсию заселенности уровней, и, если газ находится в оптическом резонаторе, можно получить лазерную генерацию. Энергия фотонов составляет при этом около 7,1 эВ, для переходов типа  (см. рис. 11.6) она отличается примерно на 2%. Это можно использовать для непрерывной перестройки частоты лазерного излучения путем настройки резонатора на любую из частот в излучаемом диапазоне. Энергия такого лазерного излучения составляет 20% полной энергии возбуждения, а к.п.д. лазера достигает 15%.
(см. рис. 11.6) она отличается примерно на 2%. Это можно использовать для непрерывной перестройки частоты лазерного излучения путем настройки резонатора на любую из частот в излучаемом диапазоне. Энергия такого лазерного излучения составляет 20% полной энергии возбуждения, а к.п.д. лазера достигает 15%.
4. Измерение интенсивности сплошного спектра излучения молекулы Н2.
Спектр излучения, возникающего при электрическом разряде в водородной трубке ТВС-15, снятый на кварцевом спектрографе ИСП-28 показан на рис. 11.7. Описание процессов, происходящих при электрическом разряде в водородной трубке, дано в Прил. 2.
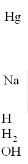

Рис. 11.7. Изображение фотопластинки со спектрами излучения водородной трубки, ртутной и натриевой ламп
Характерной особенностью спектра является наличие на пластинке области сплошного почернения – следствия сплошного спектра излучения при электронных переходах, показанных на рис. 11.6. На фоне сплошного спектра излучения водородной лампы получен спектр поглощения паров натрия (см. рис. 6.4 лабораторной работы 6). Интенсивность сплошного спектра пропорциональна интенсивности почернения фотопластинки, которую можно измерить* путем анализа компьютерного изображения с помощью свободно распространяемого графического редактора GIMP (рис. 11.8), или с помощью известного редактора Photoshop.
Выполните измерения в следующем порядке.
1. Запустите программу GIMP и откройте файл с изображением спектра. Он имеет тип полутонового изображения (в шкале яркости серого цвета – gray scale). Шкала имеет 28=256 градаций в диапазоне от 0 (черный) до 255 (белый). Яркость можно выражать также в процентах – от 0% (черный) до 100% (белый). Этого вполне достаточно для правильного отображения черно-белых фотографий. Если программа GIMP по умолчанию откроет изображение спектра в цветном режиме RGB, измените настройку командой Файл-Настройки и установите тип изображения Градации серого.
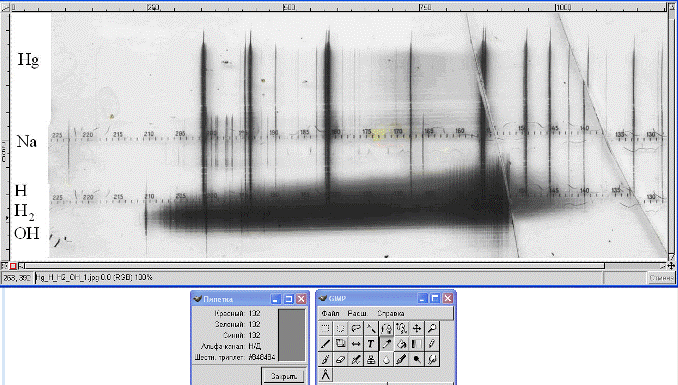
Рис. 11.8. Анализ фотоизображения спектра излучения водородной трубки в графическом редакторе GIMP (версия 1.2.3)
На палитре инструментов (рис. 11.8 внизу справа) выберите инструмент Пипетка и щелкните левой кнопкой мыши по любому месту изображения. В информационном окне инструмента Пипетка (рис. 11.8 внизу слева) будет отображена градация цвета. Таким образом, поочередно возьмите пробы цвета вдоль миллиметровой шкалы, впечатанной вдоль изображения спектра. Положение точки вдоль шкалы 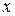 (оно указывается в мм в левом нижнем углу окна с изображением) и номер градации цвета
(оно указывается в мм в левом нижнем углу окна с изображением) и номер градации цвета 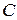 (или процент яркости) внесите в табл. 11.1. Вычислите интенсивность почернения
(или процент яркости) внесите в табл. 11.1. Вычислите интенсивность почернения 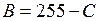 (или
(или 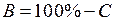 ). Определите номер градации цвета
). Определите номер градации цвета 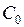 (или процент яркости) для неэкспонированной части пластинки (например, в левом верхнем углу) и найдите интенсивность ее почернения
(или процент яркости) для неэкспонированной части пластинки (например, в левом верхнем углу) и найдите интенсивность ее почернения 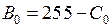 (или
(или 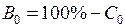 ). Вычислите интенсивность сплошного спектра − разность
). Вычислите интенсивность сплошного спектра − разность 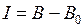 и внесите ее в табл. 11.1.
и внесите ее в табл. 11.1.
Таблица 11.1
| №
| 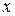 , мм , мм
| С
| 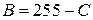 (или
(или 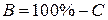 ) )
| 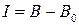
| 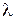 , нм , нм
| 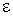 , эВ , эВ
|
| 1
|
|
|
|
|
|
|
| …
|
|
|
|
|
|
|
| …
|
|
|
|
|
|
|
2. Измерьте положение линий ртути вдоль шкалы  (в мм) и внесите результат в табл. 11.2.
(в мм) и внесите результат в табл. 11.2.
Таблица 11.2
| №
| Спектр атома
| Вблизи
деления
шкалы
| 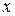 , мм , мм
| 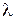 , нм , нм
| Относительная
интенсивность
|
| 1
| Na
| 225
|
| 589,3
| 4
|
| 2
| Hg
| 220
|
| 546,05
| 1
|
| 3
| 200
|
| 435,83
| 10
|
| 4
| 195
|
| 407,78
| 6
|
| 5
| 195
|
| 404,63
| 9
|
| 6
| 190
|
| 390,6
| 3
|
| 7
| 180
|
| 366,29
| 8
|
| 8
| 180
|
| 365,48
| 10
|
| 9
| 180
|
| 365,02
| 10
|
| 10
| 170
|
| 334,15
| 5
|
| 11
| 155
|
| 313,16
312,57
| 10
|
| 12
| 150
|
| 302,4
| 9
|
| 13
| 145
|
| 295,7
| 8
|
| 14
| 142
|
| 292,54
| 5
|
| 15
| 140
|
| 289,35
| 7
|
| 16
| 133
|
| 280,4
| 6
|
| 17
| 128
|
| 275,28
| 4
|
| 18
| 123
|
| 269,89
| 5
|
| 19
| 120
|
| 265,37
| 9
|
3. По данным табл. 11.2 постройте примерный градуировочный график 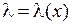 . Такой график удобно построить с помощью программы MicroCal Origin 3.0, см. Прил. 4. Если кривая получится не очень гладкой, с изломами, повторно измерьте
. Такой график удобно построить с помощью программы MicroCal Origin 3.0, см. Прил. 4. Если кривая получится не очень гладкой, с изломами, повторно измерьте  и проверьте, правильно ли сопоставлены линиям длины волн. Добейтесь получения гладкой кривой.
и проверьте, правильно ли сопоставлены линиям длины волн. Добейтесь получения гладкой кривой.
4. С помощью программы (исполняемого файла) splines.exe, выполняющей сглаживание градуировочных данных сплайнами (см. Прил. 5) определите значения длин волн для всех значений  из табл. 11.1, внесите результаты в табл. 11.1. Предварительно подберите значение параметра
из табл. 11.1, внесите результаты в табл. 11.1. Предварительно подберите значение параметра 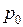 , при котором градуировочный график
, при котором градуировочный график 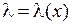 будет достаточно гладкой линией.
будет достаточно гладкой линией.
5. Определите значения энергий квантов 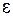 (в эВ) для длин волн из табл. 11.1 по формуле
(в эВ) для длин волн из табл. 11.1 по формуле
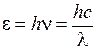 , (11.17)
, (11.17)
где 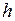 − постоянная Планка,
− постоянная Планка, 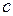 − скорость света. Для численных расчетов удобно пользоваться выражением
− скорость света. Для численных расчетов удобно пользоваться выражением
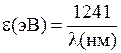 , (11.18)
, (11.18)
Для многократных расчетов по одной формуле можно воспользоваться табличным процессором Microsoft Excel (OpenOffice.org Calc) или программой MicroCal Origin 3.0 (см. Прил. 4). Внесите результаты в табл. 11.1.
6. Постройте график распределения интенсивности 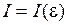 спектра сплошного излучения водородной газоразрядной трубки. Найдите наиболее вероятную, минимальную и максимальную энергии излучения.
спектра сплошного излучения водородной газоразрядной трубки. Найдите наиболее вероятную, минимальную и максимальную энергии излучения.
7. Начертите на полупрозрачной пленке отрезки с длиной, соответствующей энергии фотона 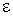 с наиболее вероятной, минимальной и максимальной энергиями излучения (в масштабе рис. 11.6а), Поочередно приложите эти три отрезка к рис. 11.6а аналогично положению отрезков
с наиболее вероятной, минимальной и максимальной энергиями излучения (в масштабе рис. 11.6а), Поочередно приложите эти три отрезка к рис. 11.6а аналогично положению отрезков 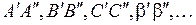 так, чтобы один конец отрезка оказался бы на верхней (
так, чтобы один конец отрезка оказался бы на верхней ( 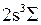 ) потенциальной кривой (среди точек
) потенциальной кривой (среди точек 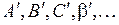 ), а другой конец – на нижней (
), а другой конец – на нижней ( 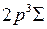 ) потенциальной кривой (среди точек
) потенциальной кривой (среди точек 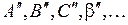 ). В таком положении отрезки будут указывать соответственно наиболее вероятные и граничные электронные переходы. Найдите колебательные уровни терма
). В таком положении отрезки будут указывать соответственно наиболее вероятные и граничные электронные переходы. Найдите колебательные уровни терма 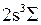 , пересекающие потенциальную кривую вблизи верхнего конца отрезков. Такие колебательные уровни молекулы заселяются с большими вероятностями. Найдите наиболее вероятные колебательные квантовые числа и наиболее вероятные колебательные энергии.
, пересекающие потенциальную кривую вблизи верхнего конца отрезков. Такие колебательные уровни молекулы заселяются с большими вероятностями. Найдите наиболее вероятные колебательные квантовые числа и наиболее вероятные колебательные энергии.
8. Постройте график распределения Больцмана (11.16) для 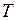 =600К и объясните с его помощью найденные значения колебательных квантовых чисел заселенных состояний терма
=600К и объясните с его помощью найденные значения колебательных квантовых чисел заселенных состояний терма 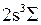 .
.





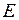 может быть приближенно представлена суммой трех энергий: электронной
может быть приближенно представлена суммой трех энергий: электронной 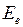 , колебательной
, колебательной 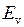 (индекс v от англ. vibration – колебание) и вращательной
(индекс v от англ. vibration – колебание) и вращательной 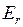 (индекс r от англ. rotation – вращение),
(индекс r от англ. rotation – вращение),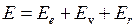 , (11.1)
, (11.1)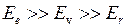 . В данной работе рассматриваются только электронная и колебательная энергия - основные слагаемые в формуле 11.1), изучению вращательной энергии посвящена работа 4.6.
. В данной работе рассматриваются только электронная и колебательная энергия - основные слагаемые в формуле 11.1), изучению вращательной энергии посвящена работа 4.6.
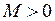 момента импульса электрона на ось молекулы ОА, вращению в противоположном направлении соответствует отрицательная проекция момента
момента импульса электрона на ось молекулы ОА, вращению в противоположном направлении соответствует отрицательная проекция момента 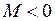 . Нижняя траектория соответствует нулевой проекции
. Нижняя траектория соответствует нулевой проекции 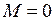 .
.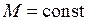 . При квантовом описании проекция момента импульса электрона на ось молекулы квантуется
. При квантовом описании проекция момента импульса электрона на ось молекулы квантуется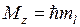 ,
, 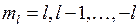 , (11.2)
, (11.2)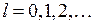 − орбитальное квантовое число. Решение уравнения Шредингера для энергий и волновых функций электрона в поле двух ядер приводит к молекулярным состояниям, называемым молекулярными орбиталями (МО). Состояния с квантовыми числами
− орбитальное квантовое число. Решение уравнения Шредингера для энергий и волновых функций электрона в поле двух ядер приводит к молекулярным состояниям, называемым молекулярными орбиталями (МО). Состояния с квантовыми числами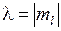 ,
, 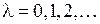 , (11.3)
, (11.3) ,
, 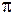 ,
, 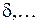 по аналогии с латинскими буквами s,p,d,…, для обозначений состояний с
по аналогии с латинскими буквами s,p,d,…, для обозначений состояний с 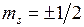 ) возможны два состояния, отличающиеся знаком проекции момента на ось (
) возможны два состояния, отличающиеся знаком проекции момента на ось ( 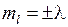 ), в качественной классической картине этому соответствует два направления вращения электрона вокруг оси молекулы. В данной работе рассматриваются только такие состояния молекулы водорода, у которых оба электрона находятся в
), в качественной классической картине этому соответствует два направления вращения электрона вокруг оси молекулы. В данной работе рассматриваются только такие состояния молекулы водорода, у которых оба электрона находятся в 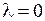 , а модуль проекции полного орбитального момента электронов на ось молекулы
, а модуль проекции полного орбитального момента электронов на ось молекулы 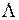 равен нулю
равен нулю 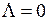 . Такие состояния (термы) обозначаются заглавной греческой буквой
. Такие состояния (термы) обозначаются заглавной греческой буквой 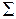 , см. табл. П9.3 в Прил. 9. Сложение спинов двух электронов по правилу сложения моментов (см. работу 10) дает два возможных значения полного спина
, см. табл. П9.3 в Прил. 9. Сложение спинов двух электронов по правилу сложения моментов (см. работу 10) дает два возможных значения полного спина 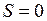 и
и 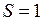 . В первом случае состояния называются синглетными, во втором – триплетными. Полный спин
. В первом случае состояния называются синглетными, во втором – триплетными. Полный спин 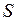 молекулы, как и у атома, принято приводить в форме мультиплетности
молекулы, как и у атома, принято приводить в форме мультиплетности 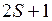 , которая указывается вверху слева от символа терма, например
, которая указывается вверху слева от символа терма, например 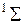 ,
, 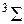 , так же как у атомных термов, например
, так же как у атомных термов, например 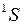 ,
, 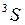 , см. работу 10 и рис. 10.4.
, см. работу 10 и рис. 10.4.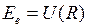 от межъядерного расстояния
от межъядерного расстояния 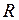 называется потенциальной функцией, а ее график – потенциальной кривой. Величину
называется потенциальной функцией, а ее график – потенциальной кривой. Величину 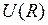 для молекулы водорода можно представить в виде суммы энергии
для молекулы водорода можно представить в виде суммы энергии 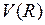 электростатического отталкивания атомных ядер (протонов) и энергии электронной подсистемы
электростатического отталкивания атомных ядер (протонов) и энергии электронной подсистемы 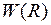 в поле ядер
в поле ядер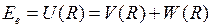 ,
, 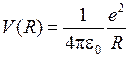 , (11.4)
, (11.4)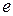 - элементарный заряд. Схематичные изображения некоторых потенциальных кривых
- элементарный заряд. Схематичные изображения некоторых потенциальных кривых 
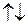 ) и двух триплетных (
) и двух триплетных ( 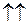 ) состояний молекулы водорода Н2. Горизонтальными отрезками обозначены низколежащие колебательные состояния
) состояний молекулы водорода Н2. Горизонтальными отрезками обозначены низколежащие колебательные состояния
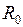 =0.074 нм. Глубина потенциальной ямы синглетного состояния
=0.074 нм. Глубина потенциальной ямы синглетного состояния 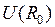 приблизительно равна энергии диссоциации – распада молекулы на атомы
приблизительно равна энергии диссоциации – распада молекулы на атомы 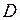 =4.48 эВ (точнее см. формулу (11.11)). Асимптотическое значение электронной энергии
=4.48 эВ (точнее см. формулу (11.11)). Асимптотическое значение электронной энергии 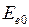 при
при 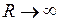 равно сумме энергий двух атомов водорода с электронами в основном состоянии с главным квантовым числом
равно сумме энергий двух атомов водорода с электронами в основном состоянии с главным квантовым числом 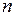 =1 (в состоянии 1s). Кривая 2 отвечает триплетному неустойчивому состоянию, переходящему при
=1 (в состоянии 1s). Кривая 2 отвечает триплетному неустойчивому состоянию, переходящему при 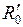 =0,1 нм. Асимптотическое значение электронной энергии
=0,1 нм. Асимптотическое значение электронной энергии 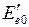 при
при 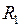 до
до 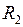 , где
, где 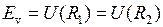 (рис. 11.3).
(рис. 11.3).
 потенциальная кривая близка к параболе
потенциальная кривая близка к параболе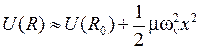 ,
, 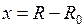 , (11.5)
, (11.5)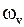 ,
,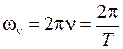 , (11.6)
, (11.6)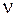 и периодом
и периодом 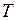 . Приведенная масса молекулы с массами атомов
. Приведенная масса молекулы с массами атомов 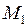 и
и 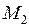
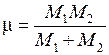 , (11.7)
, (11.7)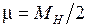 , (11.8)
, (11.8)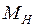 – масса ядра атома водорода. С ростом энергии
– масса ядра атома водорода. С ростом энергии 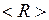 смещается от
смещается от 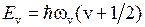 ,
, 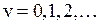 , (11.9)
, (11.9)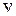 – колебательное квантовое число. Колебательные уровни
– колебательное квантовое число. Колебательные уровни 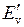 для двух электронных энергий
для двух электронных энергий 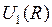 и
и 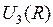 показаны на рис. 11.2. Минимальная колебательная энергия (называемая также энергией нулевых колебаний) равна
показаны на рис. 11.2. Минимальная колебательная энергия (называемая также энергией нулевых колебаний) равна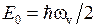 , (11.10)
, (11.10)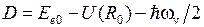 . (11.11)
. (11.11)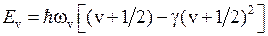 ,
, 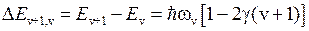 , (11.13)
, (11.13)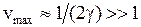 , (11.14)
, (11.14)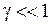 называется коэффициентом ангармоничности.
называется коэффициентом ангармоничности.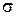 указывает, что при сближении ядер,
указывает, что при сближении ядер, 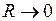 и гипотетическом образовании из них “объединенного ядра” с зарядом
и гипотетическом образовании из них “объединенного ядра” с зарядом 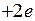 эта молекулярная орбиталь (МО) непрерывно перешла бы в основное состояние электрона в поле “объединенного ядра” – в атомную орбиталь (АО) 1s. Из-за малости межъядерного расстояния
эта молекулярная орбиталь (МО) непрерывно перешла бы в основное состояние электрона в поле “объединенного ядра” – в атомную орбиталь (АО) 1s. Из-за малости межъядерного расстояния 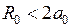 , где
, где 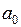 – боровский радиус,
– боровский радиус, 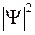 на рис. 11.4 (
на рис. 11.4 ( 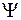 – волновая функция электрона). Одно из поперечных сечений содержит межъядерную ось (рис. 11.4а), другое перпендикулярно ей (рис. 11.4б).
– волновая функция электрона). Одно из поперечных сечений содержит межъядерную ось (рис. 11.4а), другое перпендикулярно ей (рис. 11.4б).
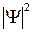 (
( 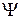 − волновая функция электрона) для МО 1s
− волновая функция электрона) для МО 1s  а б в
а б в
 . Знак волновой функции (– или +) указан одинарной или двойной штриховкой.
. Знак волновой функции (– или +) указан одинарной или двойной штриховкой.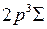 ), кривой 3 – конфигурация 1s
), кривой 3 – конфигурация 1s 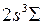 ). Переход молекулы из вышележащего устойчивого возбужденного состояния
). Переход молекулы из вышележащего устойчивого возбужденного состояния 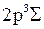 с испусканием света разрешен правилами отбора. Именно таким переходам обусловлен, в основном, сплошной спектр излучения молекулы Н2. Точные потенциальные кривые
с испусканием света разрешен правилами отбора. Именно таким переходам обусловлен, в основном, сплошной спектр излучения молекулы Н2. Точные потенциальные кривые 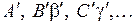 , так же как на рис. 11.2 показаны пять колебательных уровней
, так же как на рис. 11.2 показаны пять колебательных уровней 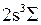 с квантовыми числами
с квантовыми числами 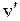 =0,1,2,3,4, Для их энергий применима формула (11.9) линейного осциллятора. Концы отрезков
=0,1,2,3,4, Для их энергий применима формула (11.9) линейного осциллятора. Концы отрезков 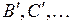 и
и 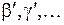 – это точки поворота, ограничивающие область, доступную для движения ядер водорода по законам классической механики. Справа вверху показана волновая функция
– это точки поворота, ограничивающие область, доступную для движения ядер водорода по законам классической механики. Справа вверху показана волновая функция 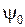 основного колебательного состояния, она быстро стремится к нулю при удалении от точек поворота в глубь классически недоступной области.
основного колебательного состояния, она быстро стремится к нулю при удалении от точек поворота в глубь классически недоступной области.

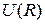 возбужденных состояний (термов)
возбужденных состояний (термов) 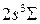 ,
, 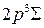 молекулы Н2 [15, рис. 9.6], [23] (а) и волновые функции основного состояния терма
молекулы Н2 [15, рис. 9.6], [23] (а) и волновые функции основного состояния терма 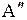 потенциальной кривой [12] (б).
потенциальной кривой [12] (б).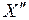 . Для энергии терма
. Для энергии терма 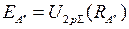 точка
точка 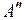 является точкой поворота
является точкой поворота 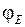 *.
*.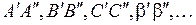 указывают некоторые наиболее вероятные электронные переходы, происходящие настолько быстро, что межъядерное расстояние не успевает измениться (в соответствии с принципом Франка-Кондона). Длины этих отрезков (в эВ) равны энергиям
указывают некоторые наиболее вероятные электронные переходы, происходящие настолько быстро, что межъядерное расстояние не успевает измениться (в соответствии с принципом Франка-Кондона). Длины этих отрезков (в эВ) равны энергиям 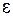 излучаемых при переходах фотонов. Поскольку энергия фотонов при таких переходах принимает непрерывный ряд значений из некоторого интервала, спектр излучения будет сплошным в некотором диапазоне длин волн. Соответствующие переходам межъядерные расстояния
излучаемых при переходах фотонов. Поскольку энергия фотонов при таких переходах принимает непрерывный ряд значений из некоторого интервала, спектр излучения будет сплошным в некотором диапазоне длин волн. Соответствующие переходам межъядерные расстояния 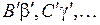 ), заселенных с большой вероятностью согласно распределению Больцмана
), заселенных с большой вероятностью согласно распределению Больцмана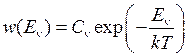 , (11.15)
, (11.15)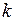 − постоянная Больцмана,
− постоянная Больцмана, 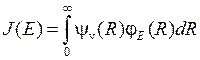 , (11.16)
, (11.16)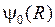 ,
, 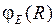 для перехода
для перехода 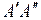 показаны на рис. 11.6б. В соответствии с формулой (11.16) наиболее вероятны переходы в такие состояния
показаны на рис. 11.6б. В соответствии с формулой (11.16) наиболее вероятны переходы в такие состояния 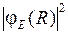 (лежащий чуть правее точки поворота) находится примерно на том же межъядерном расстоянии
(лежащий чуть правее точки поворота) находится примерно на том же межъядерном расстоянии 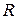 , что и максимум
, что и максимум 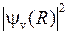 (см. рис.11.6).
(см. рис.11.6).


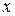 (оно указывается в мм в левом нижнем углу окна с изображением) и номер градации цвета
(оно указывается в мм в левом нижнем углу окна с изображением) и номер градации цвета 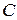 (или процент яркости) внесите в табл. 11.1. Вычислите интенсивность почернения
(или процент яркости) внесите в табл. 11.1. Вычислите интенсивность почернения 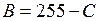 (или
(или 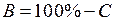 ). Определите номер градации цвета
). Определите номер градации цвета 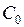 (или процент яркости) для неэкспонированной части пластинки (например, в левом верхнем углу) и найдите интенсивность ее почернения
(или процент яркости) для неэкспонированной части пластинки (например, в левом верхнем углу) и найдите интенсивность ее почернения 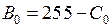 (или
(или 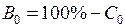 ). Вычислите интенсивность сплошного спектра − разность
). Вычислите интенсивность сплошного спектра − разность 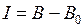 и внесите ее в табл. 11.1.
и внесите ее в табл. 11.1.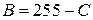 (или
(или 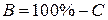 )
)
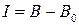
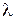 , нм
, нм
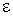 , эВ
, эВ
 (в мм) и внесите результат в табл. 11.2.
(в мм) и внесите результат в табл. 11.2.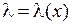 . Такой график удобно построить с помощью программы MicroCal Origin 3.0, см. Прил. 4. Если кривая получится не очень гладкой, с изломами, повторно измерьте
. Такой график удобно построить с помощью программы MicroCal Origin 3.0, см. Прил. 4. Если кривая получится не очень гладкой, с изломами, повторно измерьте  , при котором градуировочный график
, при котором градуировочный график  , (11.17)
, (11.17)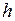 − постоянная Планка,
− постоянная Планка,  − скорость света. Для численных расчетов удобно пользоваться выражением
− скорость света. Для численных расчетов удобно пользоваться выражением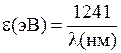 , (11.18)
, (11.18)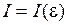 спектра сплошного излучения водородной газоразрядной трубки. Найдите наиболее вероятную, минимальную и максимальную энергии излучения.
спектра сплошного излучения водородной газоразрядной трубки. Найдите наиболее вероятную, минимальную и максимальную энергии излучения. ), а другой конец – на нижней (
), а другой конец – на нижней (  ). В таком положении отрезки будут указывать соответственно наиболее вероятные и граничные электронные переходы. Найдите колебательные уровни терма
). В таком положении отрезки будут указывать соответственно наиболее вероятные и граничные электронные переходы. Найдите колебательные уровни терма 


