Энергия молекулы 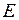 может быть приближенно представлена суммой трех энергий: электронной
может быть приближенно представлена суммой трех энергий: электронной 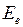 , колебательной
, колебательной 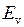 (индекс v от англ. vibration – колебание) и вращательной
(индекс v от англ. vibration – колебание) и вращательной 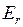 (индекс r от англ. rotation – вращение)
(индекс r от англ. rotation – вращение)
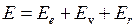 , (13.1)
, (13.1)
причем обычно 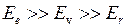 . При изменении энергии молекулы от значения
. При изменении энергии молекулы от значения 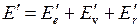 до значения
до значения 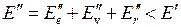 энергия испущенного фотона равна
энергия испущенного фотона равна
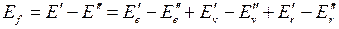 (13.2)
(13.2)
причем 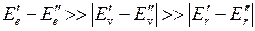 . В данной работе исследуется спектр излучения молекулы ОН, для которой
. В данной работе исследуется спектр излучения молекулы ОН, для которой 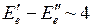 эВ. Такой спектр лежит в ближней ультрафиолетовой области и представляет собой полосы, структура которых определяется изменением электронной, колебательной и, главным образом, вращательной энергий.
эВ. Такой спектр лежит в ближней ультрафиолетовой области и представляет собой полосы, структура которых определяется изменением электронной, колебательной и, главным образом, вращательной энергий.
Качественное представление о движении ядер (атомных остовов) дает рис. 13.2. Вращение ядер вокруг оси ОВ, перпендикулярной оси молекулы ОА показано на рис. 13.2а, а сочетание вращения и колебаний - на рис. 13.2б.
|
а
б
| 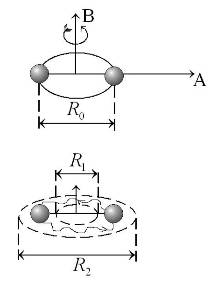
| Рис. 13.2. Качественная картина вращения (а) и сочетания вращения и колебаний (б) атомных ядер в двухатомной молекуле. Случаю (а) соответствует модель ротатора.
|
При вращении бесструктурной двухатомной молекулы с неизменным межъядерным расстоянием 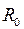 (ротатора, см. рис. 13.2а) вращательная энергия
(ротатора, см. рис. 13.2а) вращательная энергия 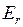 выражается через квадрат момента импульса
выражается через квадрат момента импульса 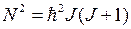
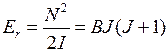 ,
, 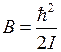 , (13.3)
, (13.3)
где 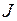 – вращательное квантовое число, принимающее значения
– вращательное квантовое число, принимающее значения 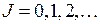 ,
,
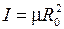 – момент инерции двухатомной молекулы с массами атомов
– момент инерции двухатомной молекулы с массами атомов 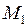 ,
, 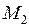 и приведенной массой
и приведенной массой
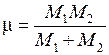 . (13.4)
. (13.4)
В различных электронных состояниях расстояния 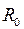 и вращательные постоянные
и вращательные постоянные 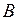 могут быть различным. Поэтому при переходах между ними с испусканием фотона изменение вращательной энергии составляет
могут быть различным. Поэтому при переходах между ними с испусканием фотона изменение вращательной энергии составляет
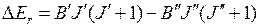 ,
, 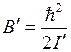 ,
, 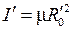 ,
, 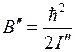 ,
, 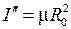 , (13.5)
, (13.5)
причем из-за правила отбора 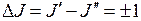 . Переходы с
. Переходы с 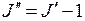 , приводящие ослаблению вращения молекулы называют переходами R -типа, а переходы с усилением ее вращения с
, приводящие ослаблению вращения молекулы называют переходами R -типа, а переходы с усилением ее вращения с 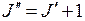 - переходами P -типа (см. рис. 13.3а). Множество спектральных линий для переходов обоих типов образуют вращательную полосу, схематично показанную на рис. 13.3г. Наличие полос является характерным признаком спектров двухатомных (и ряда других) молекул*.
- переходами P -типа (см. рис. 13.3а). Множество спектральных линий для переходов обоих типов образуют вращательную полосу, схематично показанную на рис. 13.3г. Наличие полос является характерным признаком спектров двухатомных (и ряда других) молекул*.
У некоторых вращательных полос есть характерные резкие края, называемые кантами (на рис. 13.3г кант на правом краю полосы). Они могут дать определенные сведения о свойствах молекул. Причину образования канта продемонстрируем на примере перехода R-типа с изменением вращательной энергии (13.5) с 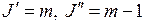 ,
, 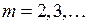
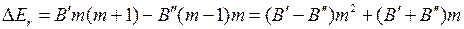 , (13.6)
, (13.6)
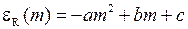 ,
, 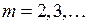 , (13.7)
, (13.7)
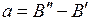 ,
, 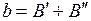 ,
, 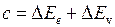 . (13.8)
. (13.8)
График зависимости 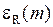 (13.7) в системе координат с осью абсцисс
(13.7) в системе координат с осью абсцисс 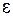 и осью ординат
и осью ординат 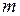 называется R-ветвью параболы Фортра. График R-ветви на рис. 6.3б показан для случая
называется R-ветвью параболы Фортра. График R-ветви на рис. 6.3б показан для случая 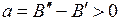 . Видно, что канту, обусловленному сгущением конечного числа спектральных линий, соответствует вершина параболы, лежащая на R-ветви. Число линий вблизи канта конечно в отличие от границ серий в спектрах атомов (см. работы 5, 6).
. Видно, что канту, обусловленному сгущением конечного числа спектральных линий, соответствует вершина параболы, лежащая на R-ветви. Число линий вблизи канта конечно в отличие от границ серий в спектрах атомов (см. работы 5, 6).
Переходы P-типа с 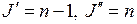 ,
, 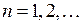 также дадут параболический график (P -ветвь) в системе координат (
также дадут параболический график (P -ветвь) в системе координат ( 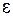 ,
, 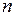 )
)
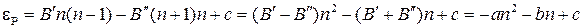 .(13.9)
.(13.9)
При замене переменных 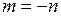 уравнение P-ветви совпадет с (13.7)
уравнение P-ветви совпадет с (13.7)
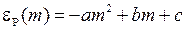 ,
, 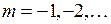 . (13.10)
. (13.10)
Таким образом, R и P ветви образуют одну параболу Фортра (см. рис. 13.3) с системой линий спектра при 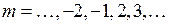 ., пустым промежутком при
., пустым промежутком при 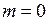 , называемом нулевой линией или началом полосы, и отсутствующей линией с
, называемом нулевой линией или началом полосы, и отсутствующей линией с 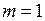 .
.
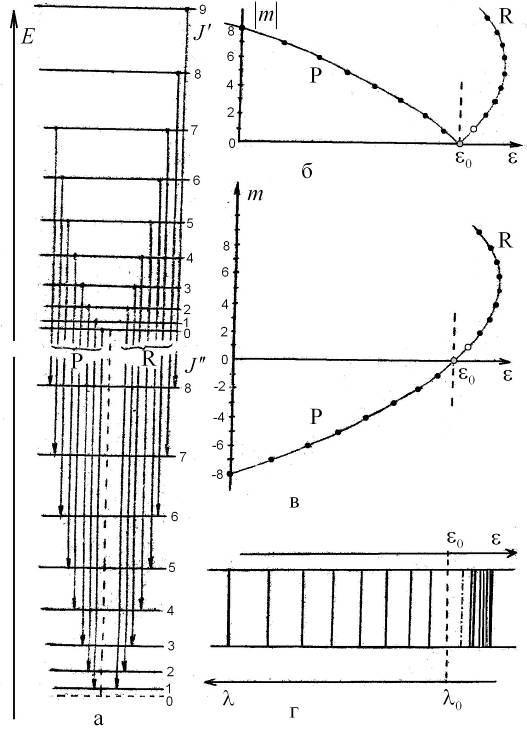
Рис. 13.3. Вращательные переходы P- и R-типа (а), парабола Фортра (б,в) и кант в полосатом молекулярном спектре (г) в модели ротатора; штриховая линия − началом полосы, штрихпунктирная линия − отсутствующая линия с 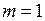
В показанном на рис. 13.3 случае 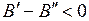 имеется кант со стороны больших энергий фотонов
имеется кант со стороны больших энергий фотонов 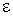 (более коротких волн
(более коротких волн 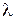 ). В противоположном случае
). В противоположном случае 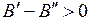 вершина параболы Фортра будет находиться на участке P-ветви, а кант будет располагаться со стороны меньших энергий фотонов
вершина параболы Фортра будет находиться на участке P-ветви, а кант будет располагаться со стороны меньших энергий фотонов 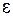 (более длинных волн
(более длинных волн 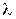 ). Вершине параболы Фортра соответствует значение вращательного квантового числа
). Вершине параболы Фортра соответствует значение вращательного квантового числа
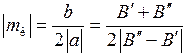 , (13.11)
, (13.11)
поэтому при малых значениях 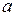
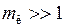 и для возможности наблюдения канта в спектре необходимо возбуждение вращательных состояний молекулы с большими квантовыми числами
и для возможности наблюдения канта в спектре необходимо возбуждение вращательных состояний молекулы с большими квантовыми числами 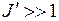 . Наличию канта и значению
. Наличию канта и значению 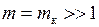 соответствует и большая протяженность вращательной полосы, ширину интервала энергий испускаемых фотонов можно оценить по формуле
соответствует и большая протяженность вращательной полосы, ширину интервала энергий испускаемых фотонов можно оценить по формуле
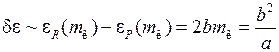 . (13.12)
. (13.12)
Поэтому полосатые спектры, включающие протяженные полосы с кантами, являются характерными признаками излучения двухатомных молекул.
В примере, показанном на рис. 13.3 наиболее удаленными от кантов являются линии Р-ветви. Интервалы между ее соседними линиями
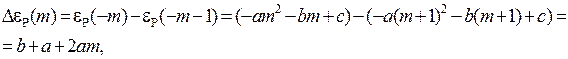 (13.13)
(13.13)
изменяются по линейному закону с удалением от начала полосы.





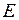 может быть приближенно представлена суммой трех энергий: электронной
может быть приближенно представлена суммой трех энергий: электронной 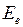 , колебательной
, колебательной 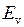 (индекс v от англ. vibration – колебание) и вращательной
(индекс v от англ. vibration – колебание) и вращательной 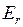 (индекс r от англ. rotation – вращение)
(индекс r от англ. rotation – вращение)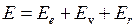 , (13.1)
, (13.1)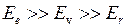 . При изменении энергии молекулы от значения
. При изменении энергии молекулы от значения 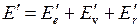 до значения
до значения 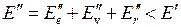 энергия испущенного фотона равна
энергия испущенного фотона равна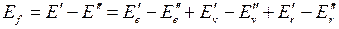 (13.2)
(13.2)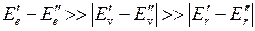 . В данной работе исследуется спектр излучения молекулы ОН, для которой
. В данной работе исследуется спектр излучения молекулы ОН, для которой 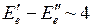 эВ. Такой спектр лежит в ближней ультрафиолетовой области и представляет собой полосы, структура которых определяется изменением электронной, колебательной и, главным образом, вращательной энергий.
эВ. Такой спектр лежит в ближней ультрафиолетовой области и представляет собой полосы, структура которых определяется изменением электронной, колебательной и, главным образом, вращательной энергий.
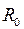 (ротатора, см. рис. 13.2а) вращательная энергия
(ротатора, см. рис. 13.2а) вращательная энергия 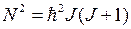
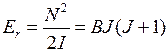 ,
, 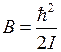 , (13.3)
, (13.3)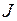 – вращательное квантовое число, принимающее значения
– вращательное квантовое число, принимающее значения 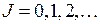 ,
,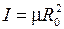 – момент инерции двухатомной молекулы с массами атомов
– момент инерции двухатомной молекулы с массами атомов 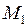 ,
, 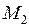 и приведенной массой
и приведенной массой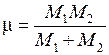 . (13.4)
. (13.4)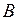 могут быть различным. Поэтому при переходах между ними с испусканием фотона изменение вращательной энергии составляет
могут быть различным. Поэтому при переходах между ними с испусканием фотона изменение вращательной энергии составляет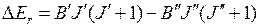 ,
, 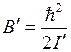 ,
, 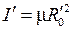 ,
, 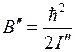 ,
, 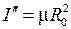 , (13.5)
, (13.5)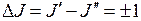 . Переходы с
. Переходы с 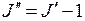 , приводящие ослаблению вращения молекулы называют переходами R -типа, а переходы с усилением ее вращения с
, приводящие ослаблению вращения молекулы называют переходами R -типа, а переходы с усилением ее вращения с 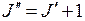 - переходами P -типа (см. рис. 13.3а). Множество спектральных линий для переходов обоих типов образуют вращательную полосу, схематично показанную на рис. 13.3г. Наличие полос является характерным признаком спектров двухатомных (и ряда других) молекул*.
- переходами P -типа (см. рис. 13.3а). Множество спектральных линий для переходов обоих типов образуют вращательную полосу, схематично показанную на рис. 13.3г. Наличие полос является характерным признаком спектров двухатомных (и ряда других) молекул*.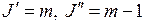 ,
, 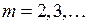
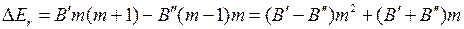 , (13.6)
, (13.6)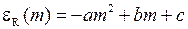 ,
, 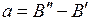 ,
, 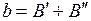 ,
, 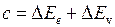 . (13.8)
. (13.8)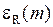 (13.7) в системе координат с осью абсцисс
(13.7) в системе координат с осью абсцисс 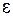 и осью ординат
и осью ординат 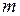 называется R-ветвью параболы Фортра. График R-ветви на рис. 6.3б показан для случая
называется R-ветвью параболы Фортра. График R-ветви на рис. 6.3б показан для случая 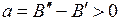 . Видно, что канту, обусловленному сгущением конечного числа спектральных линий, соответствует вершина параболы, лежащая на R-ветви. Число линий вблизи канта конечно в отличие от границ серий в спектрах атомов (см. работы 5, 6).
. Видно, что канту, обусловленному сгущением конечного числа спектральных линий, соответствует вершина параболы, лежащая на R-ветви. Число линий вблизи канта конечно в отличие от границ серий в спектрах атомов (см. работы 5, 6).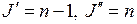 ,
, 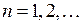 также дадут параболический график (P -ветвь) в системе координат (
также дадут параболический график (P -ветвь) в системе координат ( 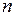 )
)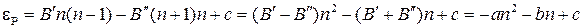 .(13.9)
.(13.9)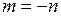 уравнение P-ветви совпадет с (13.7)
уравнение P-ветви совпадет с (13.7)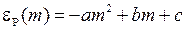 ,
, 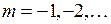 . (13.10)
. (13.10)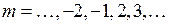 ., пустым промежутком при
., пустым промежутком при 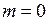 , называемом нулевой линией или началом полосы, и отсутствующей линией с
, называемом нулевой линией или началом полосы, и отсутствующей линией с 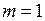 .
.
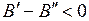 имеется кант со стороны больших энергий фотонов
имеется кант со стороны больших энергий фотонов 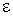 (более коротких волн
(более коротких волн 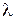 ). В противоположном случае
). В противоположном случае 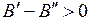 вершина параболы Фортра будет находиться на участке P-ветви, а кант будет располагаться со стороны меньших энергий фотонов
вершина параболы Фортра будет находиться на участке P-ветви, а кант будет располагаться со стороны меньших энергий фотонов 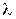 ). Вершине параболы Фортра соответствует значение вращательного квантового числа
). Вершине параболы Фортра соответствует значение вращательного квантового числа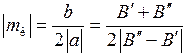 , (13.11)
, (13.11)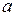
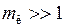 и для возможности наблюдения канта в спектре необходимо возбуждение вращательных состояний молекулы с большими квантовыми числами
и для возможности наблюдения канта в спектре необходимо возбуждение вращательных состояний молекулы с большими квантовыми числами 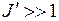 . Наличию канта и значению
. Наличию канта и значению 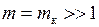 соответствует и большая протяженность вращательной полосы, ширину интервала энергий испускаемых фотонов можно оценить по формуле
соответствует и большая протяженность вращательной полосы, ширину интервала энергий испускаемых фотонов можно оценить по формуле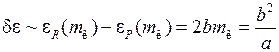 . (13.12)
. (13.12)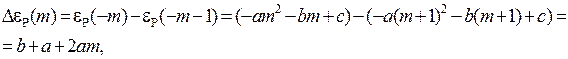 (13.13)
(13.13)

