

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Интересное:
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Теорема Котельникова лежит в основе любой цифровой системы.
При рассмотрении процесса дискретизации можно видеть, что при 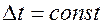 (равномерная дискретизация), сигнал
(равномерная дискретизация), сигнал 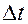 – амплитудно-импульсный (амплитудно-импульсная модуляция, АИМ)
– амплитудно-импульсный (амплитудно-импульсная модуляция, АИМ)
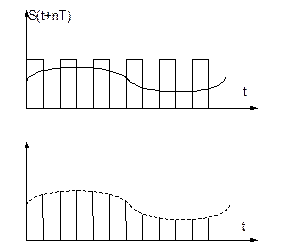 |
Импульсная несущая
АИМ
Название модуляции (аналоговая и импульсная) дают по виду несущей. У импульсной несущей можно менять 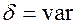 , получим широтно-импульсную модуляцию (ШИМ) Если
, получим широтно-импульсную модуляцию (ШИМ) Если 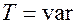 , то
, то 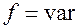 , получаем частотно-импульсную модуляцию (ЧИМ). Если
, получаем частотно-импульсную модуляцию (ЧИМ). Если 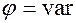 , получаем фазово-импульсную модуляцию (ФИМ).
, получаем фазово-импульсную модуляцию (ФИМ).
Т.к. 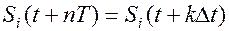 , то это – индивидуальные импульсные несущие. Импульсная несущая и ее составляющие ортогональны.
, то это – индивидуальные импульсные несущие. Импульсная несущая и ее составляющие ортогональны.
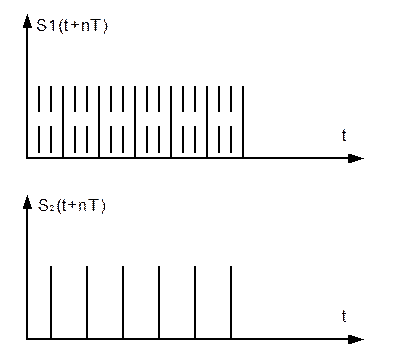
Спектр импульсно-модулированных сигналов определяется спектром импульсных несущих. Независимо от вида модуляции спектр импульсно-модулированных сигналов есть симметричный спектр импульсной последовательности (т.е. несущей)
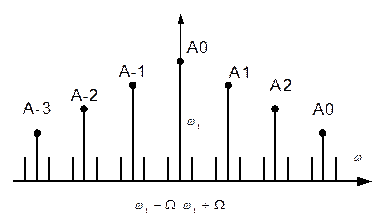
Модулированное колебание
Особенностью является спектр при АИМ, симметричный, относительно любой модулирующей составляющей, кроме нулевой. А спектр аналога модулированного сигнала определяется характером несущей составляющей.
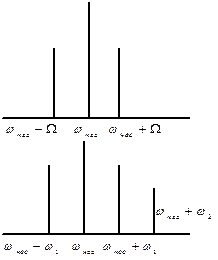
ТЕОРЕМЫ О СПЕКТРАХ
Приведем теперь без доказательства, несколько теорем о спектрах, выражающие основные свойства преобразования Фурье.
1) Теорема сложения. Спектр суммы нескольких сигналов равен сумме спектров этих сигналов.
2) Теорема запаздывания. Спектральная плотность сигнала 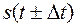 полученного при сдвиге сигнала
полученного при сдвиге сигнала 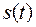 по оси времени на
по оси времени на 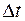 , определяется выражением
, определяется выражением
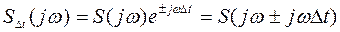
т.е. сдвиг функции по оси времени приводит к появлению фазового сдвига для всех частотных составляющих, равного 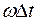 .
.
3) Теорема смещения. Если 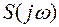 - спектр функции
- спектр функции 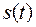 , то спектру
, то спектру 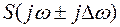 полученному путем сдвига исходного спектра по оси частот на величину
полученному путем сдвига исходного спектра по оси частот на величину 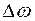 , соответствует функция
, соответствует функция
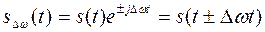
4) Теорема о спектрах производной и интеграла. Спектры производной и интеграла от функции 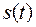 определяются выражениями
определяются выражениями
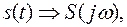
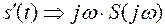
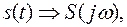
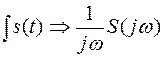
5) Теорема о спектре произведения. Спектр произведения двух функций S1(t) и S2(t) определяется операцией свертки их спектров:
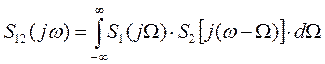
|
|
|

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!