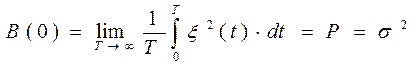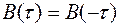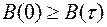Флуктуационная помеха – множество случайных последовательностей импульсов, которые накладываются друг на друга. Флуктуационная (Гауссовская) помеха характеризуется нормальным законом распределения вероятностей амплитудных значений.
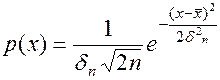
Это выражение справедливо для одномерной плотности.  -плотность – плотность вероятности.
-плотность – плотность вероятности.
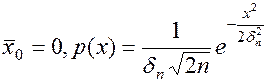
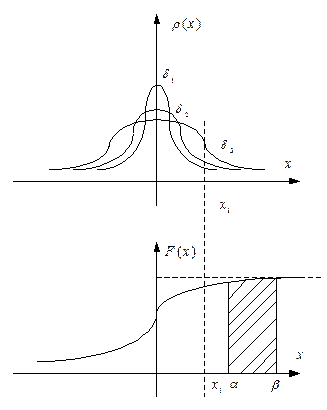
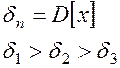
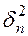 - мощность флуктуационной помехи
- мощность флуктуационной помехи
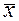 - среднее значение или постоянная составляющая;
- среднее значение или постоянная составляющая;
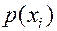 - вероятность того, что амплитудное значение флуктуационной помехи попадет в интервал
- вероятность того, что амплитудное значение флуктуационной помехи попадет в интервал 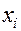 ;
;
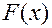 – вероятность того, что все значения флуктуационной помехи
– вероятность того, что все значения флуктуационной помехи
будут лежать левее 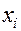 ;
;
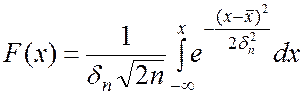 - этот интеграл вычисляется через табулированную функцию Лапласа
- этот интеграл вычисляется через табулированную функцию Лапласа 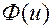 ,
,
Часто возникает задача вычисления попадания флуктуационной помехи в интервал от 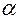 до
до 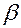 , вероятность попадания которой равна:
, вероятность попадания которой равна:
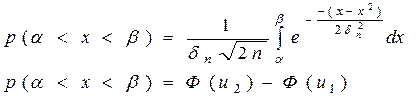
Существует несколько видов функции Лапласа: которая задается от - 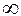 до
до 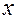 и от
и от 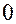 до
до 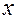 .
.
Т.к. нормальный закон распределения известен, достаточно знать параметры: среднее значение (постоянная составляющая) и среднеквадратическое отклонение (мощность помехи)
Характеристический спектр флуктуационной помехи должен быть нормально распределен.
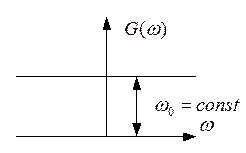
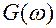 – мощность помехи на 1 Гц частоты.
– мощность помехи на 1 Гц частоты.
Если спектр задан на бесконечном интервале, то помеха называется белым шумом, т.е. это широкополосный шум.
Если ширина шума 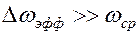 , то можно принять помеху за белый шум.
, то можно принять помеху за белый шум.
Интервал корреляции 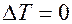 , если это идеальный белый шум, т.е. все отдельные значения этой функции независимы друг от друга, т.е. некоррелированы, и такую функцию можно назвать функцией Дирака.
, если это идеальный белый шум, т.е. все отдельные значения этой функции независимы друг от друга, т.е. некоррелированы, и такую функцию можно назвать функцией Дирака.
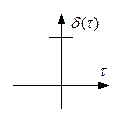
Если 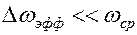 , то помеха называется окрашенным шумом.
, то помеха называется окрашенным шумом.
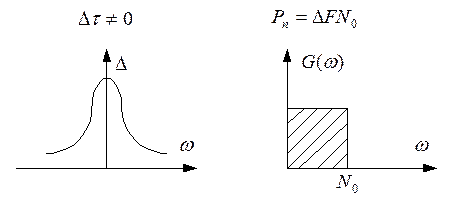
Степень случайности значений функции помехи можно определить через интервал корреляции – это интервал, на который отстают две помехи. Чем больше 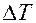 , тем процесс более случайный.
, тем процесс более случайный.
ФУНКЦИЯ КОРЕЛЛЯЦИИ
Одной из важнейших характеристик случайного процесса является функция корреляции (иначе - функция автокорреляции), которая учитывает статистическую зависимость между значениями случайного процесса в различные моменты времени. ФК определяется как математическое ожидание от произведения значений процесса в два различные момента времени
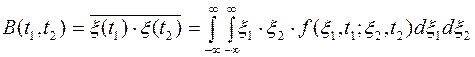 (1)
(1)
где 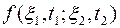 - двумерная плотность распределения
- двумерная плотность распределения
вероятностей процесса 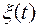 .
.
Анализируя данное выражение, замечаем, что величина интеграла будет больше в тех случаях, когда с увеличением (уменьшением) значений процесса в момент времени 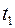 будут также увеличиваться (уменьшаться) значения процесса в момент времени
будут также увеличиваться (уменьшаться) значения процесса в момент времени 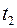 . Следовательно, корреляционная функция определяет степень линейной зависимости между значениями случайного процесса в различные моменты времени. Чем быстрее изменяется случайный процесс, тем меньшее значение будет иметь функция корреляции при фиксированных моментах времени
. Следовательно, корреляционная функция определяет степень линейной зависимости между значениями случайного процесса в различные моменты времени. Чем быстрее изменяется случайный процесс, тем меньшее значение будет иметь функция корреляции при фиксированных моментах времени 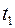 и
и 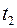 .
.
Перечислим важнейшие свойства функции автокорреляции (корреляции) для стационарных случайных процессов с нулевым математическим ожиданием:
1. В пределе, при 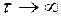 , значения реализации случайного процесса становятся статистически независимыми, следовательно предельное значение функции корреляции
, значения реализации случайного процесса становятся статистически независимыми, следовательно предельное значение функции корреляции 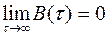 .
.
2. При 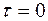 , выражение (5) превращается в формулу для вычисления мощности (иначе - дисперсии) реализации случайного процесса, т.е.
, выражение (5) превращается в формулу для вычисления мощности (иначе - дисперсии) реализации случайного процесса, т.е.
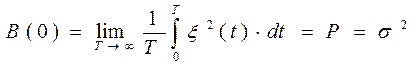
3. Функция корреляции является четной функцией, т.е.
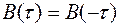
что следует из свойства инвариантности к направлению временного сдвига плотности распределения стационарного случайного процесса
4. Корреляционная функция всегда максимальна при 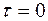 .
.
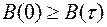





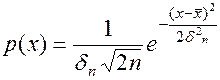
 -плотность – плотность вероятности.
-плотность – плотность вероятности.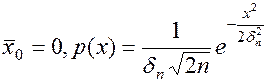
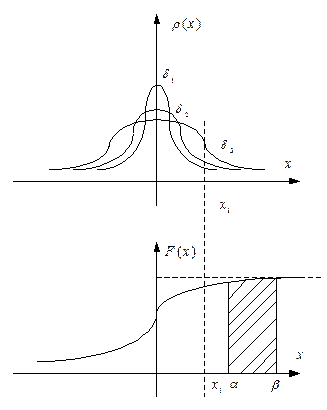
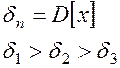
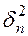 - мощность флуктуационной помехи
- мощность флуктуационной помехи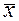 - среднее значение или постоянная составляющая;
- среднее значение или постоянная составляющая;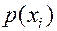 - вероятность того, что амплитудное значение флуктуационной помехи попадет в интервал
- вероятность того, что амплитудное значение флуктуационной помехи попадет в интервал 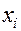 ;
;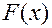 – вероятность того, что все значения флуктуационной помехи
– вероятность того, что все значения флуктуационной помехи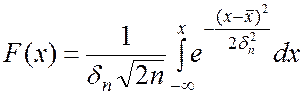 - этот интеграл вычисляется через табулированную функцию Лапласа
- этот интеграл вычисляется через табулированную функцию Лапласа 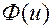 ,
,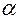 до
до 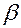 , вероятность попадания которой равна:
, вероятность попадания которой равна: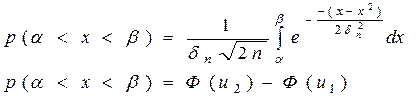
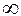 до
до 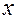 и от
и от 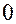 до
до 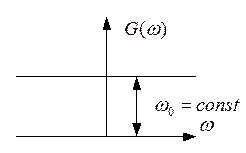
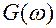 – мощность помехи на 1 Гц частоты.
– мощность помехи на 1 Гц частоты.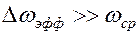 , то можно принять помеху за белый шум.
, то можно принять помеху за белый шум.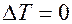 , если это идеальный белый шум, т.е. все отдельные значения этой функции независимы друг от друга, т.е. некоррелированы, и такую функцию можно назвать функцией Дирака.
, если это идеальный белый шум, т.е. все отдельные значения этой функции независимы друг от друга, т.е. некоррелированы, и такую функцию можно назвать функцией Дирака.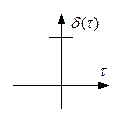
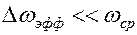 , то помеха называется окрашенным шумом.
, то помеха называется окрашенным шумом.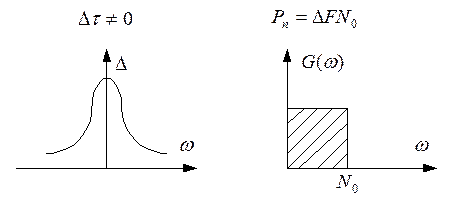
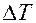 , тем процесс более случайный.
, тем процесс более случайный.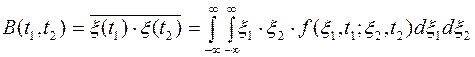 (1)
(1)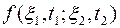 - двумерная плотность распределения
- двумерная плотность распределения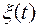 .
.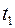 будут также увеличиваться (уменьшаться) значения процесса в момент времени
будут также увеличиваться (уменьшаться) значения процесса в момент времени 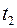 . Следовательно, корреляционная функция определяет степень линейной зависимости между значениями случайного процесса в различные моменты времени. Чем быстрее изменяется случайный процесс, тем меньшее значение будет иметь функция корреляции при фиксированных моментах времени
. Следовательно, корреляционная функция определяет степень линейной зависимости между значениями случайного процесса в различные моменты времени. Чем быстрее изменяется случайный процесс, тем меньшее значение будет иметь функция корреляции при фиксированных моментах времени 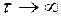 , значения реализации случайного процесса становятся статистически независимыми, следовательно предельное значение функции корреляции
, значения реализации случайного процесса становятся статистически независимыми, следовательно предельное значение функции корреляции 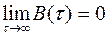 .
.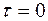 , выражение (5) превращается в формулу для вычисления мощности (иначе - дисперсии) реализации случайного процесса, т.е.
, выражение (5) превращается в формулу для вычисления мощности (иначе - дисперсии) реализации случайного процесса, т.е.