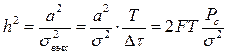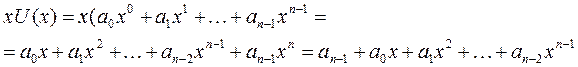Сигнал и помеху можно представить как вектор. При геометрическом представлении кодированных сигналов. Широко use n-мерное пространство в Неевклидовой метрике. Расстояние в этом пространстве определяется по алгоритму 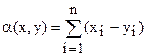 , n- число элементов комбинации данного кода, а xi и yi –значения соответствующих разрядов. Геометрической моделью n - значного двоичного кода является n-мерный куб с ребром = 1, каждая из вершин которого представляет одну из возможных комбинаций. 000,001,010,100,101,110,011,111 Расстояние -
, n- число элементов комбинации данного кода, а xi и yi –значения соответствующих разрядов. Геометрической моделью n - значного двоичного кода является n-мерный куб с ребром = 1, каждая из вершин которого представляет одну из возможных комбинаций. 000,001,010,100,101,110,011,111 Расстояние - 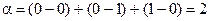 . Кодированный сигнал в виде n-мерного куба.
. Кодированный сигнал в виде n-мерного куба.
Удобной формой представления сигналов и помех является геометрическая форма.Действительно, сигнал в сигнальном пространстве может быть представлен совокупностью чисел (число отчетов, гармоник).
n →x1, x2,……..xm Аналогично можно представить и помеху.В общем случае:


Действует аддитивная помеха x(t)=S(t)+W(t)
Если под воздействием помехи результирующий вектор, содержащий xi, не пересекает пространство сигнала x(t) 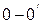 , то ошибки нет. Если пересекает, то появляется ошибка при приёме.
, то ошибки нет. Если пересекает, то появляется ошибка при приёме.
Если помеха аналоговая (белый шум) с произвольной амплитудой и фазой, то в сигнальном пространстве это будет круг (на плоскости), иначе будет шар, если m величин.
Если попадается на границу 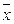 , то повторяет передачу.
, то повторяет передачу.
Один из важных параметров – угол α12 между векторами.
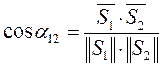
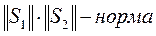
1) При ортогональной системе векторов
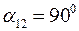
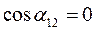
2) При 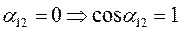
3) При 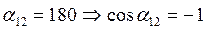
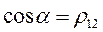 – это коэффициент корреляции, коэффициент статистической связи.
– это коэффициент корреляции, коэффициент статистической связи.
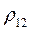 – изменяется от –1 до 1 и определяет различимость сигналов при различных видах модуляции.
– изменяется от –1 до 1 и определяет различимость сигналов при различных видах модуляции.
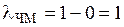
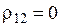
1. При ЧМ
2. При ФМ
3. При АМ
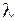 - коэффициент различимости.
- коэффициент различимости.
Интегральный прием.
| СВ, помеха на выходе интегратора
| |
Для сигнала в виде прям-ых импульсов метод синхронного накопления можно осуществить, если операцию дискр-го сумм-ия отсчетов заменить операцией непрерывного интегрирования на интер-вале сущ-ия сигнала.
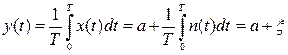
Эфф. полоса пропускания: 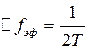 . Если шум на выходе имеет мощность σ2 (в полосе F > Δfэф), мощность шума на выходе самого интегратора < в F/Δfэф
. Если шум на выходе имеет мощность σ2 (в полосе F > Δfэф), мощность шума на выходе самого интегратора < в F/Δfэф

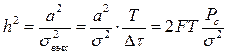
При интегральном приеме h2 > в N = T/Δτ = 2FT, N – число независимых значений помехи на
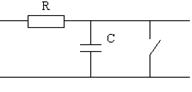
интервале (0; T). Это означает, что дискр-ое сумм-ие и интегр-ие обеспеч-ют одинаковый результат. Однако практически операция интегрирования осуществляется проще. В качестве интегратора может исп-ся RC-цепь.
| В ней С синхронно разряжается в конце каждой посылки. Если на вход подают радиоимпульс, то интегр-ие осущ-ся коммутируемым разонатором, например, колебательным контуром с высокой добротностью.
| |
Метод накопления суммированием или интегр-ем может быть осуществлён и при передаче одного и того же сигнала по нескольким независимым каналам (в к-ых действ. независим. помеха).
ЦИКЛИЧЕСКИЕ ( n , k) КОДЫ
Линейный ( n , k) код называется циклическим, если при циклическом сдвиге символов кодовой комбинации на один разряд вправо (влево) образуются комбинации, также принадлежащие коду.
Для алгебраического описания циклических ( n k ) кодов каждой комбинации U = (a 1 , а2, а3, ..., an) ставится в соответствие многочлен (полином) U ( x ) = a 0 x 0 + a 1 x 1 + a 2 x 2 + ... + an -1 xn -1 от формальной переменной х. Умножение на х увеличивает степень многочлена U ( x ) и вызывает удлинение кодовой комбинации на один символ. Чтобы избежать увеличения степени U ( x ), xn заменяют на 1 (х n = 1 или xn – 1 = 0):
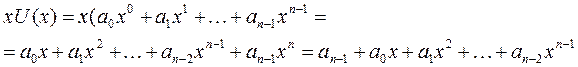
Для множества многочленов, соответствующих n-символьным комбинациям, вводятся операции сложения, вычитания, умножения, совпадающие с обычными операциями над многочленами. Сложение коэффициентов многочлена выполняется по модулю 2, при этом операции сложения и вычитания совпадают. Умножение многочленов выполняется по модулю многочлена x' – 1, причем x' – 1 = x n + 1. Таким образом, для описания и построения циклических кодов используется алгебра многочленов по модулю x n + 1, называемому модулем по умножению.
При представлении кодовых комбинаций многочленами, циклическим ( n , k ) кодом называется множество многочленов Ui ( x ) степени не больше п – 1, которые делятся без остатка на некоторый многочлен g ( x ) степени n – k, называемый производящим (порождающим).
Многочлен g ( x ) является производящим для циклического (n, k) кода, если он является делителем многочлена x n + 1, т. е.
xn + 1 = g ( x ) h ( x ),
где h ( x ) – многочлен степени k, называемый проверочным многочленом ( n , k ) кода, который также как и g ( x ) задает циклический (n, k) код.
Циклический ( n , k ) код имеет минимальное кодовое расстояние dmin, если вес комбинации, соответствующий производящему многочлену g ( x ), не менее dmin. Это означает, что количество слагаемых производящего многочлена g ( x ) должно быть не менее dmin .
Производящий многочлен g ( x ) циклического кода, исправляющий однократные ошибки, является неприводимым, т. е. делится сам на себя и на 1. Для исправления ошибок большей кратности g ( x ) раскладывается на множители gi ( x ), число которых равно кратности ошибки и каждый из них является неприводимым.





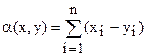 , n- число элементов комбинации данного кода, а xi и yi –значения соответствующих разрядов. Геометрической моделью n - значного двоичного кода является n-мерный куб с ребром = 1, каждая из вершин которого представляет одну из возможных комбинаций. 000,001,010,100,101,110,011,111 Расстояние -
, n- число элементов комбинации данного кода, а xi и yi –значения соответствующих разрядов. Геометрической моделью n - значного двоичного кода является n-мерный куб с ребром = 1, каждая из вершин которого представляет одну из возможных комбинаций. 000,001,010,100,101,110,011,111 Расстояние - 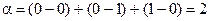 . Кодированный сигнал в виде n-мерного куба.
. Кодированный сигнал в виде n-мерного куба.

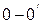 , то ошибки нет. Если пересекает, то появляется ошибка при приёме.
, то ошибки нет. Если пересекает, то появляется ошибка при приёме.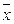 , то повторяет передачу.
, то повторяет передачу.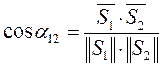
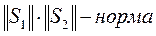
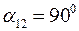
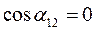
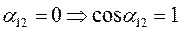
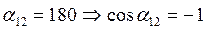
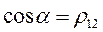 – это коэффициент корреляции, коэффициент статистической связи.
– это коэффициент корреляции, коэффициент статистической связи.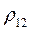 – изменяется от –1 до 1 и определяет различимость сигналов при различных видах модуляции.
– изменяется от –1 до 1 и определяет различимость сигналов при различных видах модуляции.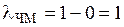
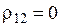
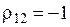
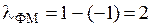
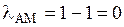
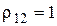
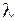 - коэффициент различимости.
- коэффициент различимости.
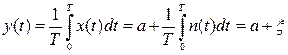
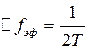 . Если шум на выходе имеет мощность σ2 (в полосе F > Δfэф), мощность шума на выходе самого интегратора < в F/Δfэф
. Если шум на выходе имеет мощность σ2 (в полосе F > Δfэф), мощность шума на выходе самого интегратора < в F/Δfэф