Важнейшим классом случайных процессов, встречающихся на практике, является класс стационарных случайных процессов. Случайный процесс называется стационарным в узком смысле, если его многомерная функция распределения (и, следовательно, числовые характеристики) не зависят от начала отсчета времени. При этом оказывается, что одномерная функция распределения, среднее значение и дисперсия, вообще не зависят от времени, а двумерная функция распределения, и корреляционная функция зависят только от разности времен 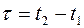 .
.
Иногда случайный процесс называют стационарным в широком смысле, если приведенные условия выполняются лишь для числовых характеристик. Узкое и широкое определения, стационарности не тождественны. Случайные процессы, стационарные в узком смысле, всегда стационарны и в широком смысле, но не наоборот.
Если приведенные выше условия не выполняются, то случайный процесс будет нестационарным. Для нестационарного случайного процесса плотность вероятности является функцией времени. При этом со временем могут изменяться среднее значение, дисперсия, или то и другое вместе.
Временные характеристики случайных процессов в общем случае будут различными для различных реализаций. Исключение составляют так называемые эргодические процессы, для которых временные характеристики для всех реализаций одинаковы. Кроме того, для эргодических процессов временные характеристики, полученные из одной единственной реализации путем усреднения по времени, с вероятностью, сколь угодно близкой к единице, совпадают с соответствующими характеристиками, полученными путем усреднения по множеству (ансамблю) реализаций в один момент времени. Следовательно, для эргодических процессов справедливы равенства:
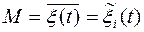
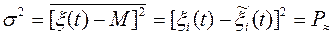
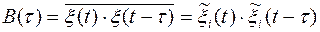
Существует теорема, согласно которой стационарные процессы при достаточно общих предположениях, являются одновременно и эргодическими.
Свойство эргодичности стационарных случайных процессов имеет большое практическое значение. Для таких процессов любая реализация полностью определяет свойства всего процесса в целом. Это позволяет при определении статистических характеристик случайного процесса ограничиться рассмотрением лишь одной реализации достаточно большой длительности, как это и делается в настоящей лабораторной работе при определении одномерной плотности вероятности.
Корреляционный прием.
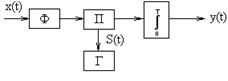
| Сигнал поступает на входной Ф на перемножитель. Результат перемножения – на интегратор. Г – гетеродин, выдает мест-ную копию переданного сигнала, отсчет и решение произво-дится в момент окончания интегр-ия.
| |
Сигнал на выходе приемника: 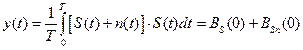 , где BS(0) – мощность сигнала, BSn(0) – ф-ия вз. корреляции двух независимых процессов: помехи и опорного сигнала.
, где BS(0) – мощность сигнала, BSn(0) – ф-ия вз. корреляции двух независимых процессов: помехи и опорного сигнала.
В качестве опорного исп-ся задержанный принимаемый сигнал
τз = τпосылки
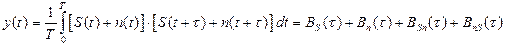
| |
Исп-ие набора коррелятора позволяет осущ-ть полное разделение нескольких ортогональных сиг-налов на [0; Т]. Если идет передача модулированных импульсов(манипулированных сигналов) по частоте и фазе, соотв-ая частота и фаза колебаний местного гетеродина должна быть равна частоте и фазе приним-ых сигналов. В этом случае рассматр-ая схема одновр. Выполняет ф-ии детектирования. Такой детектор наз-ют
синхронным или
когерентным. Такой приемник обеспе-чивает max возможную помехоустойчивость. В том случае, когда формирование местного опор-ного сигнала с точностью до потенциала высокочаст-ой составляющей затруднено, исп-ся
автоко-рреляционный приемник.
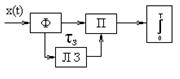
Автокоррел. приемник по помехоуст. уступает коррел-му. В обоих случаях для уменьшения уровня различных помех исп-ся узкополосная ф-ия. При приеме манипулиров. сигнал Ф может стоять какдо детектора, так и после. При когерентном приеме додетект. и последет. ф-ии равн-оценны. При некогерентном ф-ия до детектора обеспеч. более высокую помехоуст-ть, чем ф-ия после детектора.
Все рассматриваемые методы обеспеч. практич. одинаковые рез-ты.
| общее выражение для всех способов
приема
| |
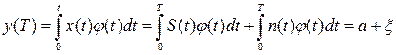
x(t) = S(t) + n(t),
φ(t) – весовая ф-ия, определяющая способ приема, при интегральном приеме φ(t) = 1, при коррел. и когерентном приемах φ(t) = S(t), при автокоррел. φ(t) = x(t + τ), оптим-ый Ф: φ(t) = S(Т – τ)
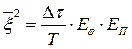 , где Еφ – энергия φ(t), ЕП – энергия помехи, Δτ – интервал коррел. помехи. φ(t) должна выбираться из условия max полезного сигнала.
, где Еφ – энергия φ(t), ЕП – энергия помехи, Δτ – интервал коррел. помехи. φ(t) должна выбираться из условия max полезного сигнала.
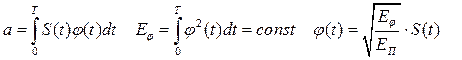
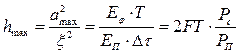 при когерентном приеме
при когерентном приеме
Мультипликативная помеха
при действии на сигнал перемножается 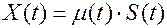
Мультипликативная помеха возникает из-за изменения во времени амплитудных и фазовых характеристик канала, например при прохождении сигнала через среду с изменяющимися во времени параметрами, при многолучевом распространении радиоволны и т.д.
Статистические параметры
Очень часто при описании случайных процессов от функций распределения отказываются и ограничиваются лишь некоторыми числовыми характеристиками, из которых наиболее часто используются среднее значение, дисперсия и корреляционная функция.
Простейшей характеристикой случайного процесса является среднее значение или математическое ожидание
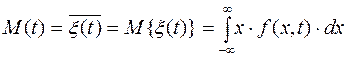
которое представляет собой неслучайную функцию, около которой различным образом располагаются реализации случайного процесса.
Дисперсией случайного процесса называется неслучайная функция, значения которой для каждого момента времени равны математическому ожиданию квадрата отклонения случайного процесса от его среднего значения:
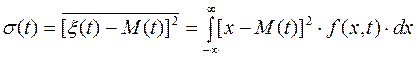 (6)
(6)
Дисперсия определяет степень разброса значений случайного процесса около среднего значения.
В качестве характеристики, учитывающей статистическую связь между значениями случайного процесса в различные моменты времени, используется автокорреляционная функция случайного процесса:
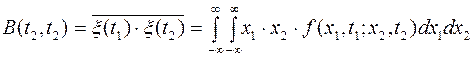
определяемая как математическое ожидание от произведения значений случайного процесса в два различных момента времени.
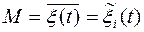
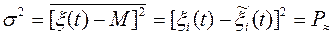
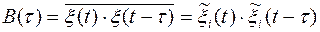
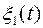 представляет собой ток или напряжение.
представляет собой ток или напряжение.





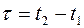 .
.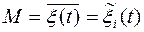
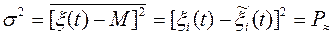
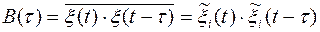

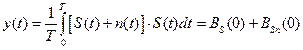 , где BS(0) – мощность сигнала, BSn(0) – ф-ия вз. корреляции двух независимых процессов: помехи и опорного сигнала.
, где BS(0) – мощность сигнала, BSn(0) – ф-ия вз. корреляции двух независимых процессов: помехи и опорного сигнала.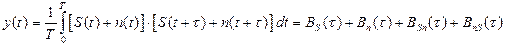

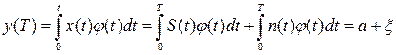
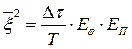 , где Еφ – энергия φ(t), ЕП – энергия помехи, Δτ – интервал коррел. помехи. φ(t) должна выбираться из условия max полезного сигнала.
, где Еφ – энергия φ(t), ЕП – энергия помехи, Δτ – интервал коррел. помехи. φ(t) должна выбираться из условия max полезного сигнала.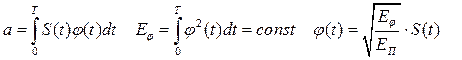
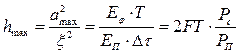 при когерентном приеме
при когерентном приеме 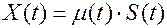
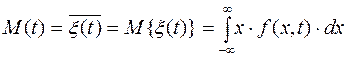
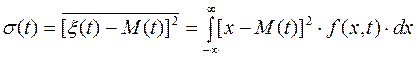 (6)
(6)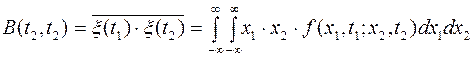
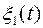 представляет собой ток или напряжение.
представляет собой ток или напряжение.


