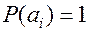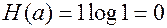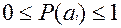В принципе все методы приёма сигналов заключаются в фильтрации (когда помеха подавляется, а полезный сигнал выделяется).
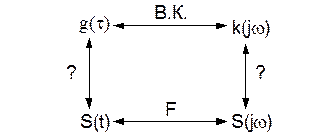 Выигрыш:
Выигрыш: 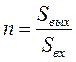
Известно:
1) Форма сигнала S(t)
2) Есть прямое и обратное преобразование Фурье
3) Фильтр – это четырёхполюсник (линейный)
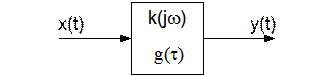
g(τ) – временная характеристика (реакция фильтра на дельта импульс).
k(jw) – комплексный коэффициент передачи по частоте.
k(jw) и g(τ) – однозначно жестко связаны законом Винера-Колмогорова.
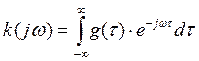
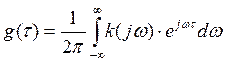
Условия согласования:
Надо:
1. 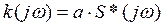
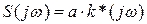
2. 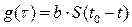
Длительность сигнала 0÷τ.
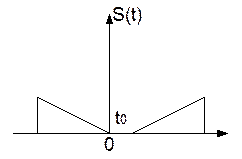
Как найти y(t), если есть x(t)=S(t)+W(t)
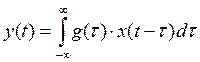
Зная процесс на выходе y(t), можно найти его мощность.
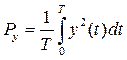
Полагая, что помеха W(t) – белый гауссовский шум с плотностью No, можно найти мощность шума. При заданной плотности S(jw) можно найти ширину спектра сигнала S(t).
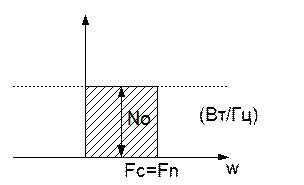
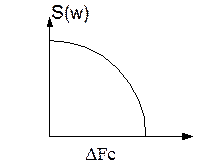
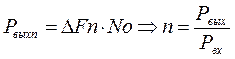
Подставим значения и зная, что длительность сигнала: 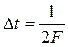
Получаем: 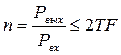
Таким образом, процесс на выходе y(t) в точности до масштабного коэффициента со сдвигом на время Т повторяет автокорреляционную функцию сигнала x(t). В этом смысле приём сигнала на согласованный фильтр аналогичен корреляционному приёму. И не надо иметь эталонный генератор, потому что его заменяют характеристики согласованного фильтра.
Шумовая полоса будет ограничена ΔFn, следовательно, шум становиться окрашенным.
Если на входе случайные процессы с различными законами распределения, то процесс на выходе будет иметь нормальный закон распределения.
Автокорреляционный приём.
x(t)=S(t)+W(t) (помеха гауссовская)
Будем искать функцию взаимной корреляции между принимаемой функцией x(t) и её задержанной копией на время τ.
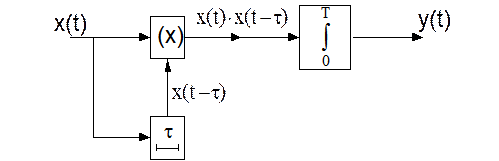
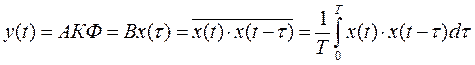
АКФ зависит от τ, а не от t.
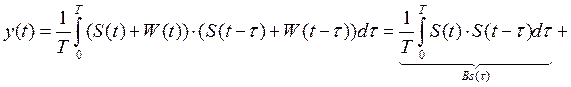
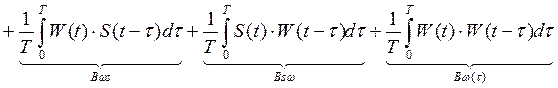
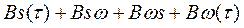 (1)
(1)
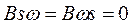
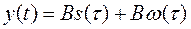 (2)
(2)
Зная, что значения сигнала сильно коррелированны.
Пусть W(t) – гауссовский шум
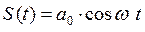
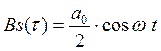

Выигрыш так же не превысит 2TF, но нет множества генераторов.
Энтропия
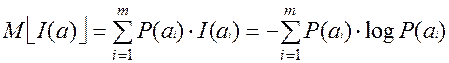 это среднее количество информации на сообщение, которое вырабатывает источник. [бит/сообщение ] эЭнтропия источника:
это среднее количество информации на сообщение, которое вырабатывает источник. [бит/сообщение ] эЭнтропия источника: 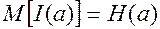 - характеризует степень неопределенности состояния источника. (Но с точки зрения получателя информации: энтропия частично или полностью уменьшается). Отсюда, энтропия - это математическое ожидание по частным количествам информации сообщений, генерируемых источником. Безусловная энтропия источника
- характеризует степень неопределенности состояния источника. (Но с точки зрения получателя информации: энтропия частично или полностью уменьшается). Отсюда, энтропия - это математическое ожидание по частным количествам информации сообщений, генерируемых источником. Безусловная энтропия источника 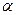 вычисляется по формуле
вычисляется по формуле
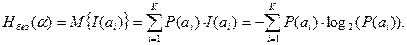 [бит/сообщ.] (8)
[бит/сообщ.] (8)
Отметим, что формула (8) не учитывает статистическую связь между символами, поэтому такая энтропия называется безусловной.
Энтропия является показателем средней априорной неопределенности при выборе очередного символа из источника. Выражение (8) можно рассматривать, как меру неопределенности (энтропии) состояния источника, заданного своими безусловными вероятностями.
Из выражения (8) следует, что энтропия источника равна нулю тогда и только тогда, когда одна из вероятностей 
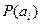 равна единице, а остальные вероятности соответственно равны нулю, т.е. когда имеет место полной определенности выбора.
равна единице, а остальные вероятности соответственно равны нулю, т.е. когда имеет место полной определенности выбора.
Свойства энтропии:
1. Максимальное значение энтропии - это когда все состояния источника равновероятны.
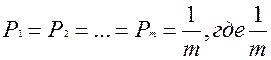 - числе состояний источника.
- числе состояний источника.
2. Энтропия равна нулю, если одно из состояний источника является достоверным событием, т.е. равна 1.
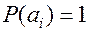
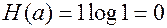
3. Энтропия всегда величина положительная (неотрицательная).
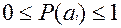
Учет статистических связей между символами, последовательно выбираемых источником ведет к дальнейшему уменьшению энтропии, определяемой формулой (8), не учитывающей этой связи. На самом деле, чем больше вероятностные связи символов, тем меньше свобода выбора последующих символов, тем меньше в среднем информации приходится на каждый вновь выбираемый символ источника и тем меньше энтропия.





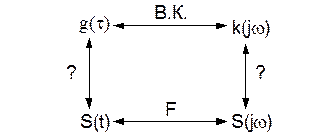 Выигрыш:
Выигрыш: 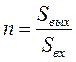
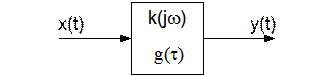
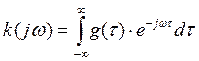
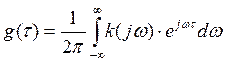
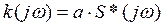
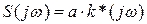
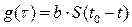
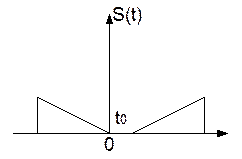
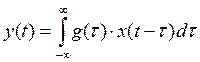
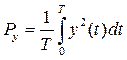

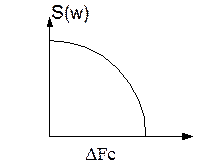
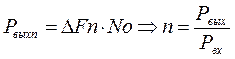
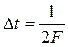
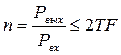
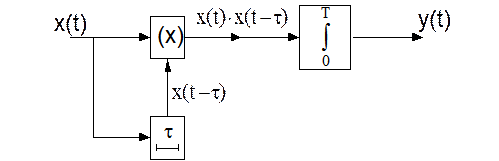
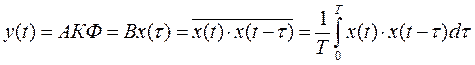
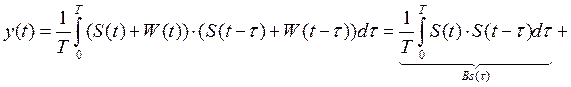
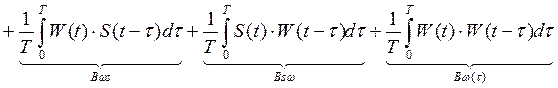
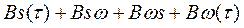 (1)
(1)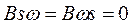
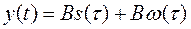 (2)
(2)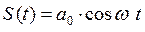
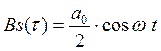

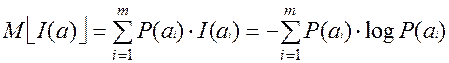 это среднее количество информации на сообщение, которое вырабатывает источник. [бит/сообщение ] эЭнтропия источника:
это среднее количество информации на сообщение, которое вырабатывает источник. [бит/сообщение ] эЭнтропия источника: 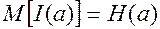 - характеризует степень неопределенности состояния источника. (Но с точки зрения получателя информации: энтропия частично или полностью уменьшается). Отсюда, энтропия - это математическое ожидание по частным количествам информации сообщений, генерируемых источником. Безусловная энтропия источника
- характеризует степень неопределенности состояния источника. (Но с точки зрения получателя информации: энтропия частично или полностью уменьшается). Отсюда, энтропия - это математическое ожидание по частным количествам информации сообщений, генерируемых источником. Безусловная энтропия источника 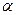 вычисляется по формуле
вычисляется по формуле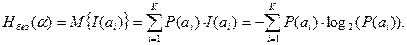 [бит/сообщ.] (8)
[бит/сообщ.] (8)
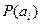 равна единице, а остальные вероятности соответственно равны нулю, т.е. когда имеет место полной определенности выбора.
равна единице, а остальные вероятности соответственно равны нулю, т.е. когда имеет место полной определенности выбора.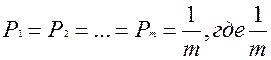 - числе состояний источника.
- числе состояний источника.