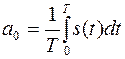Частный случай критерия минимума среднего риска. Предполагается что ошибочный приём сигнала, тем опаснее, чем реже этот сигнал передаётся. Величина потерь при этом обратно пропорциональна априорной вероятности . Use тогда, когда априорные вероятности сигналов не сильно отличаются друг от друга или неизвестны. Когда нет объективного задавания потерь и ошибок разного рода.
Минимаксный критерий.
В основе лежит критерий минимального среднего риска, согласно которому величина ср.риска зависит от распределения априорных вероятностей P(Sk), кот. стремиться к нулю, в случае, если одна из вероятностей P(Sl) стремиться к единице, а остальные- к нулю. Наименьший средний риск будет иметь максимум при некотором распределении вероятностей P*(Sk).Минимаксный критерий используют в том случае, когда P*(Sk) неизвестны. Суть: минимизируется максимально возможный риск.
Критерий Неймана-Пирсона.
Этот критерий используется в тех случаях, когда ошибки разного рода резко отличаются по последствиям (пожаротушение, радиолокация).
Критерий Неймана-Пирсона.
Этот критерий используется в тех случаях, когда ошибки разного рода резко отличаются по последствиям (пожаротушение, радиолокация). Рпц - вероятность пропуска цели. Рлт – вероятность ложной тревоги. Они не равноценны. Но пропуск цели можно учесть при следующем приёме.При разбиении пространства на 2-е большие области, всегда можно уменьшить вероятность пропуска сигнала, ценой увеличения уровня ложной тревоги и наоборот. Пространство сигналов можно разбить на область  0 – пространство отсутствия сигнала (цели),
0 – пространство отсутствия сигнала (цели),  1 - наличия.
1 - наличия.
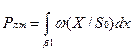 -вероятность ложной тревоги.
-вероятность ложной тревоги.
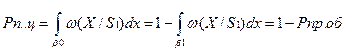 (вероятность пропуска цели)
(вероятность пропуска цели)
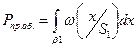 ;
;
Согласно критерию Н.П. оптимальным считается приёмник, который при заданной вероятности ложной тревоги PЛТ обеспечивает наибольшую вероятность правильного обнаружения.
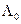 - пороговое значение отношения правдоподобия, определяется из допустимой вероятности Л.Т.
- пороговое значение отношения правдоподобия, определяется из допустимой вероятности Л.Т.
Правило принятия решения о наличие цели: 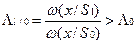 ; Use в системах обнаружения.
; Use в системах обнаружения.
Корреляционный приём.
Исп-ие набора коррелятора позволяет осущ-ть полное разделение нескольких ортогональных сиг-налов на [0; Т]. Если идет передача модулированных импульсов(манипулированных сигналов) по частоте и фазе, соотв-ая частота и фаза колебаний местного гетеродина должна быть равна частоте и фазе приним-ых сигналов. В этом случае рассматр-ая схема одновр. Выполняет ф-ии детектирования. Такой детектор наз-ют синхронным или когерентным. Такой приемник обеспе-чивает max возможную помехоустойчивость. В том случае, когда формирование местного опор-ного сигнала с точностью до потенциала высокочаст-ой составляющей затруднено, исп-ся автоко-рреляционный приемник.
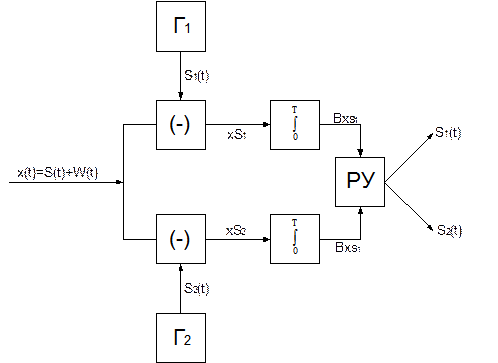
Оптимальный приёмник Котельникова эквивалентен корреляционному приёмнику, следовательно, корреляционный приёмник – оптимальный. Корреляционный метод то же оптимальный.Корреляционный метод даёт выигрыш в n=2TF раза, то приёмник Котельникова даёт такой же выигрыш.
26.Приём сигналов методом накопления.
Самый простой метод накопления – это повторение.
1 0 1 1 1 * – ошибка
 0*1*0*0*1 .
0*1*0*0*1 .
1 0 1 1 0* .
 1 0 1 1 1 .
1 0 1 1 1 .
мажорирование
Метод в таком виде не применяется. В реальности синхронное повторение (повтор не просто сообщения, а повторяется со стробированием внутри каждого сигнала n-раз).
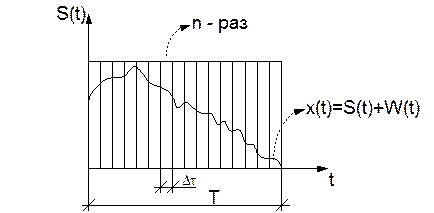
При сложении отсчетных амплитудных значений накапливается мощность, как сигнала, так и помехи. 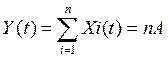 – накопленные амплитуды.
– накопленные амплитуды.
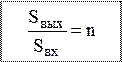
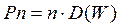
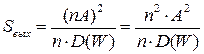
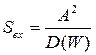
Выигрыш при синхронном повторении заключается в том, что Рп накапливается по линейному закону, а Рс по квадратичному.
В остальных случаях n не может превысить базы сигнала.
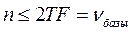
В реальности число повторений n ограничено. При n→∞ метод синхронного приёма превращается в интегральный приём.
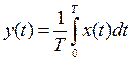 – интегральный приём.
– интегральный приём.
Реально число повторений не превышает 10 раз, а число стробов не превышает 20 раз.
Т.о. этот метод исп-ся при обнаружении любого сигна-ла, описываемого произв-ой периодической ф-ей, если брать отсчет синхронного с интервалом, равным периоду. Теоретически методом накопления можно обнаружить сколь угодно малый сигнал. Для сигнала с конечной длительностью увеличивать число отсчетов бесконечно не имеет смысла, т.к. отсчеты помех стан-ся коррелир-ми. Полученные результаты справедливы только для некоррелируемых отсчетов.
Комплексный ряд Фурье.
Кроме тригонометрической формы записи ряда Фурье весьма полезной и пожалуй более простой является комплексная или как ее иногда называют экспоненциальная форма:
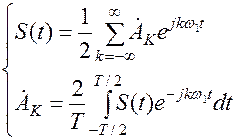
где 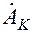 - комплексная амплитуда.
- комплексная амплитуда.
Преимущество такой формы ряда Фурье, по крайней мере, в том, что для вычисления коэффициентов ряда необходимо вычислять лишь один интеграл.Однако, следует обратить внимание на то, что сумма охватывает не только положительные значения к, но и отрицательные. Отсюда появляется понятие отрицательных частот. Тем не менее это нисколько не усложняет ситуацию, так как, если сигнал 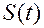 является вещественным ( а мы молчаливо это предполагаем), то из сразу же следует, что комплексная амплитуда
является вещественным ( а мы молчаливо это предполагаем), то из сразу же следует, что комплексная амплитуда 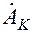 - величина, комплексно сопряженная с
- величина, комплексно сопряженная с 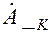 , то есть
, то есть
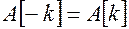
Таким образом, комплексные амплитуды компонент с отрицательной частотой определяются амплитудами компонент с положительной частотой. Еще раз подчеркнем, что это справедливо лишь, если  - вещественная функция. Если
- вещественная функция. Если 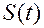 - комплексный, то естественно теряет свою справедливость. Итак, при представлении сигнала
- комплексный, то естественно теряет свою справедливость. Итак, при представлении сигнала 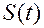 в ряд Фурье в комплексной форме - основная задача заключается в определении комплексной амплитуды
в ряд Фурье в комплексной форме - основная задача заключается в определении комплексной амплитуды 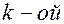 гармонической составляющей.
гармонической составляющей.
Равенство Парсеваля
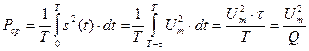 , (30)
, (30)
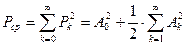 , (31)
, (31)
где 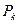 - мощности;
- мощности; 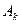 - амплитуды гармоник спектра импульсов.
- амплитуды гармоник спектра импульсов.
Используя формулы (30),(31), вводят понятие практической ширины спектра. А именно, практической шириной спектра называют такой интервал частот, в котором сосредоточена основная доля мощности, например, 95% от мощности выражаемой формулой (30). Таким образом, чтобы найти практическую ширину нужно суммировать мощности гармоник 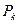 в ряде (31) до тех пор, пока, сумма не превысит значений 0.95 от величины мощности в (30). Найденный таким образом наибольший номер
в ряде (31) до тех пор, пока, сумма не превысит значений 0.95 от величины мощности в (30). Найденный таким образом наибольший номер 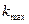 гармоники , учтенной в сумме, позволяет вычислить практическую ширину спектра как
гармоники , учтенной в сумме, позволяет вычислить практическую ширину спектра как
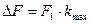 ,
,
где 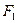 - интервал частот между гармониками, равный частоте 1-ой гармоники.
- интервал частот между гармониками, равный частоте 1-ой гармоники.
30. Из курса математики известно, что любую периодическую функцию, удовлетворяющую условиям Дирихле, можно представить рядом Фурье.
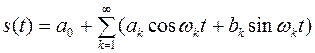
где 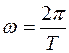 - круговая частота
- круговая частота
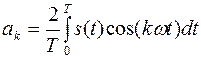 - чётные коэффициенты ряда Фурье
- чётные коэффициенты ряда Фурье
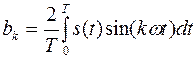 - нечётные коэффициенты ряда Фурье
- нечётные коэффициенты ряда Фурье
Величина
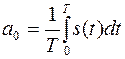
определяет среднее значение сигнала за период и называется постоянной составляющей. Частота f =1/T называется основной частотой сигнала, а кратные ей частоты fk = kf - высшими гармониками.





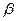 0 – пространство отсутствия сигнала (цели),
0 – пространство отсутствия сигнала (цели), 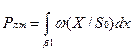 -вероятность ложной тревоги.
-вероятность ложной тревоги.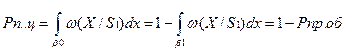 (вероятность пропуска цели)
(вероятность пропуска цели)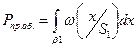 ;
;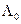 - пороговое значение отношения правдоподобия, определяется из допустимой вероятности Л.Т.
- пороговое значение отношения правдоподобия, определяется из допустимой вероятности Л.Т.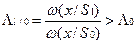 ; Use в системах обнаружения.
; Use в системах обнаружения. 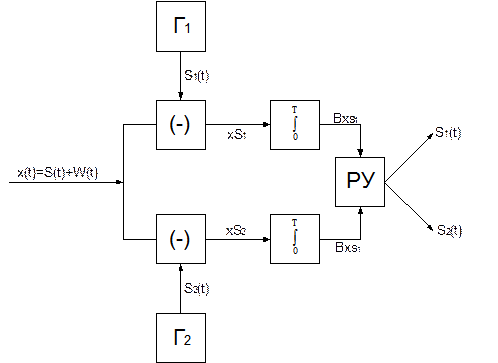
 0*1*0*0*1 .
0*1*0*0*1 . 1 0 1 1 1 .
1 0 1 1 1 .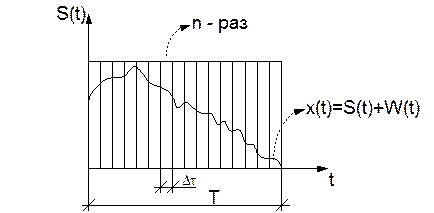
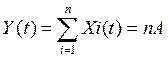 – накопленные амплитуды.
– накопленные амплитуды.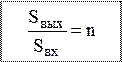
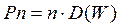
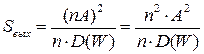
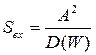
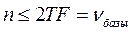
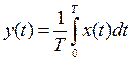 – интегральный приём.
– интегральный приём.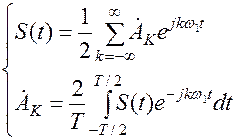
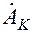 - комплексная амплитуда.
- комплексная амплитуда.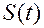 является вещественным ( а мы молчаливо это предполагаем), то из сразу же следует, что комплексная амплитуда
является вещественным ( а мы молчаливо это предполагаем), то из сразу же следует, что комплексная амплитуда 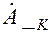 , то есть
, то есть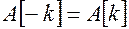
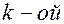 гармонической составляющей.
гармонической составляющей.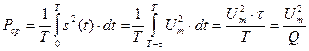 , (30)
, (30)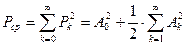 , (31)
, (31)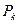 - мощности;
- мощности; 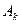 - амплитуды гармоник спектра импульсов.
- амплитуды гармоник спектра импульсов.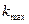 гармоники , учтенной в сумме, позволяет вычислить практическую ширину спектра как
гармоники , учтенной в сумме, позволяет вычислить практическую ширину спектра как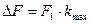 ,
, 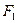 - интервал частот между гармониками, равный частоте 1-ой гармоники.
- интервал частот между гармониками, равный частоте 1-ой гармоники.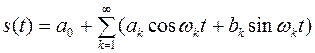
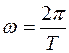 - круговая частота
- круговая частота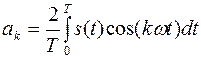 - чётные коэффициенты ряда Фурье
- чётные коэффициенты ряда Фурье 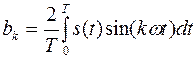 - нечётные коэффициенты ряда Фурье
- нечётные коэффициенты ряда Фурье