В соответствие с определением средняя мощность за период T прямоугольной последовательнсти импульсов выражается через интеграл
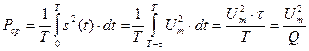 , (30)
, (30)
где 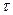 - длительность;
- длительность; 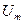 - амплитуда; Q - скважность импульсов.
- амплитуда; Q - скважность импульсов.
Другой способ нахождения средней мощности заключается в использовании равенства Парсеваля
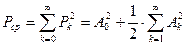 , (31)
, (31)
где 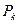 - мощности;
- мощности; 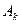 - амплитуды гармоник спектра импульсов.
- амплитуды гармоник спектра импульсов.
Используя формулы (30),(31), вводят понятие практической ширины спектра. А именно, практической шириной спектра называют такой интервал частот, в котором сосредоточена основная доля мощности, например, 95% от мощности выражаемой формулой (30). Таким образом, чтобы найти практическую ширину нужно суммировать мощности гармоник 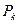 в ряде (31) до тех пор, пока, сумма не превысит значений 0.95 от величины мощности в (30).
в ряде (31) до тех пор, пока, сумма не превысит значений 0.95 от величины мощности в (30).
Энергия 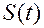 -это сумма элементарных энергий (то же самое и для мощностей).
-это сумма элементарных энергий (то же самое и для мощностей).
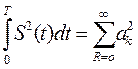
Функция 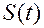 задана на конечном интервале, а сумма энергий – на бесконечном интервале.
задана на конечном интервале, а сумма энергий – на бесконечном интервале.
10.Функция отсчетов
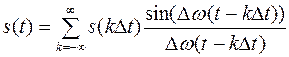
Множитель 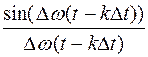 называется функцией отсчётов. Рассматривая семейство этих функций, соответствующих различным значениям
называется функцией отсчётов. Рассматривая семейство этих функций, соответствующих различным значениям 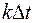 , видим, что в каждый момент времени
, видим, что в каждый момент времени 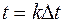 только одна функция равна 1, а все остальные равны нулю. Обладает свойством ортогональности. Ортогональные это такие функции, которые не имеют взаимной энергии, мощности (они меняются во времени) и коэффициент корреляции которых равен нулю. Идеализированная функция. Четная. Период определяется интервалом дискретизации. Спектральная плотность имеет прямоугольную форму с частотой среза F.
только одна функция равна 1, а все остальные равны нулю. Обладает свойством ортогональности. Ортогональные это такие функции, которые не имеют взаимной энергии, мощности (они меняются во времени) и коэффициент корреляции которых равен нулю. Идеализированная функция. Четная. Период определяется интервалом дискретизации. Спектральная плотность имеет прямоугольную форму с частотой среза F.
Расчет графиков спектров при аналоговой модуляции
Спектром сигнала называют функцию, показывающую зависимость интенсивности различных гармоник в составе сигнала от частоты этих гармоник. Спектр периодического сигнала – это зависимость коэффициентов ряда Фурье от частот гармоник, которым эти коэффициенты соответствуют.
Учитывая известную теорему о спектре произведения сигнала на гармоническое колебание, можно заключить, что спектр АМ сдвигается вправо по оси частот на частоту несущей, а форма спектра АМ будет повторять форму спектра модулирующего сигнала с точностью до множителя (1/2). То есть, для получения графика спектра г) необходимо:
- взять гармоники модулирующего сигнала, начиная с первой;
- умножить амплитуды гармоник на 0.5:
- расположить их на оси частот симметрично относительно частоты несущей:
- нулевую гармонику без изменений её амплитуды разместить на частоте несущей.

Спектр АМ сигнала
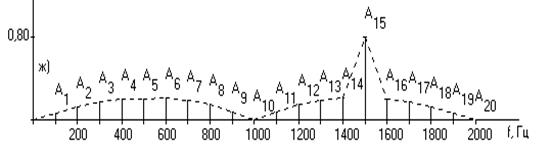
Спектр ЧМ сигнала
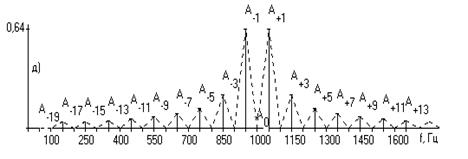
Спектр ОФМ сигнала





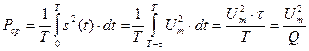 , (30)
, (30)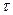 - длительность;
- длительность; 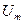 - амплитуда; Q - скважность импульсов.
- амплитуда; Q - скважность импульсов.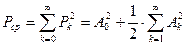 , (31)
, (31)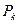 - мощности;
- мощности; 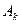 - амплитуды гармоник спектра импульсов.
- амплитуды гармоник спектра импульсов.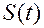 -это сумма элементарных энергий (то же самое и для мощностей).
-это сумма элементарных энергий (то же самое и для мощностей).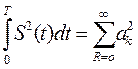
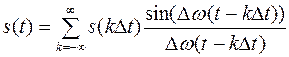
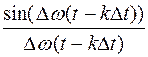 называется функцией отсчётов. Рассматривая семейство этих функций, соответствующих различным значениям
называется функцией отсчётов. Рассматривая семейство этих функций, соответствующих различным значениям 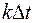 , видим, что в каждый момент времени
, видим, что в каждый момент времени 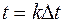 только одна функция равна 1, а все остальные равны нулю. Обладает свойством ортогональности. Ортогональные это такие функции, которые не имеют взаимной энергии, мощности (они меняются во времени) и коэффициент корреляции которых равен нулю. Идеализированная функция. Четная. Период определяется интервалом дискретизации. Спектральная плотность имеет прямоугольную форму с частотой среза F.
только одна функция равна 1, а все остальные равны нулю. Обладает свойством ортогональности. Ортогональные это такие функции, которые не имеют взаимной энергии, мощности (они меняются во времени) и коэффициент корреляции которых равен нулю. Идеализированная функция. Четная. Период определяется интервалом дискретизации. Спектральная плотность имеет прямоугольную форму с частотой среза F.





