(1) 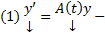 ОСЛОДУ
ОСЛОДУ
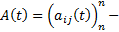 матрица непрерывна на
матрица непрерывна на 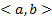 функций (коэффициенты системы). Напомним, что в ЛП столбцов функций (высоты h) столбцы
функций (коэффициенты системы). Напомним, что в ЛП столбцов функций (высоты h) столбцы 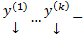 называется ЛЗ, если
называется ЛЗ, если 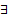 нетривиальный набор чисел
нетривиальный набор чисел 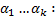 (2)
(2) 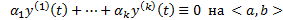 . Если тождество (2) выполняется только при
. Если тождество (2) выполняется только при 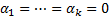 , то система
, то система 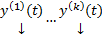 ЛНЗ
ЛНЗ
Свойства решений ОСЛОДУ
1) (Тривиальность) ОСЛОДУ (1) всегда обладает решением 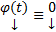 Док-во: очевидно
Док-во: очевидно
2) (Линейность) Если 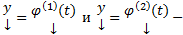 некоторые решения (1), то
некоторые решения (1), то 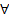 чисел
чисел 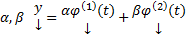 также является решением (1)
также является решением (1)
Док-во: Введем в ЛП столбцов функций оператор L: 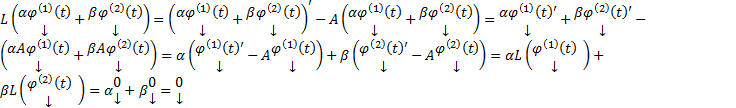 . Сейчас доказано, что L является линейным оператором и что любая ЛК решения также является решением.
. Сейчас доказано, что L является линейным оператором и что любая ЛК решения также является решением.
Замеч. Из 1) и 2) следует, что совокупность всевозможных решений ОСЛОДУ (1) образует ЛП, которое обозначим 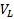
3) (О нуле решения) Если 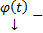 решение (1) или (3) с непрерывными коэффициентами
решение (1) или (3) с непрерывными коэффициентами 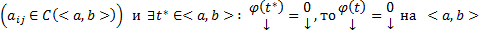
Док-во: Рассмотрим ЗК для (1) : 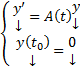 , но эта ЗК также обладает решением
, но эта ЗК также обладает решением 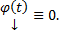
По ТСЕ получаем 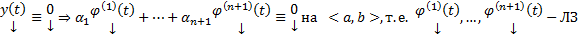
5) (О линейной независимости)
ОСЛОДУ (1) (или (3)) с непрерывными коэффициентами обладает n ЛНЗ решениями
Док-во: Рассмотрим набор столбцов : 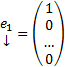 ,
, 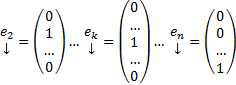 и рассмотрим n штук ЗК :
и рассмотрим n штук ЗК : 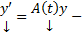 ОСЛОДУ
ОСЛОДУ
(3) 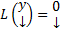
Опр. Любой базис в 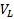 назовем фундаментальной системой решений (ФСР) : ОСЛОДУ (1) (или(3)). Т.е. ФСР это упорядоченный набор из n ЛНЗ решений ОСЛОДУ (и всякое решение может быть передано как ЛК элементов этого набора)
назовем фундаментальной системой решений (ФСР) : ОСЛОДУ (1) (или(3)). Т.е. ФСР это упорядоченный набор из n ЛНЗ решений ОСЛОДУ (и всякое решение может быть передано как ЛК элементов этого набора)
6) (Об общем решении ОСЛОДУ)
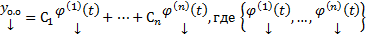 назовем ФСР ОСЛОДУ,
назовем ФСР ОСЛОДУ, 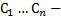 произвольные постоянные
произвольные постоянные
Док-во: 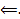 Поскольку
Поскольку 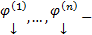 базис, то любое решение является ЛК
базис, то любое решение является ЛК 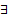
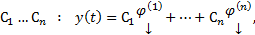
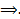 Из свойства линейности любая ЛК
Из свойства линейности любая ЛК 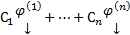 является решением.
является решением.





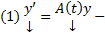 ОСЛОДУ
ОСЛОДУ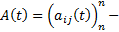 матрица непрерывна на
матрица непрерывна на 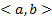 функций (коэффициенты системы). Напомним, что в ЛП столбцов функций (высоты h) столбцы
функций (коэффициенты системы). Напомним, что в ЛП столбцов функций (высоты h) столбцы 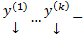 называется ЛЗ, если
называется ЛЗ, если 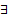 нетривиальный набор чисел
нетривиальный набор чисел 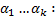 (2)
(2) 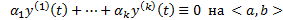 . Если тождество (2) выполняется только при
. Если тождество (2) выполняется только при 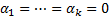 , то система
, то система 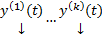 ЛНЗ
ЛНЗ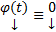 Док-во: очевидно
Док-во: очевидно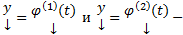 некоторые решения (1), то
некоторые решения (1), то 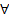 чисел
чисел 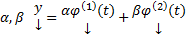 также является решением (1)
также является решением (1)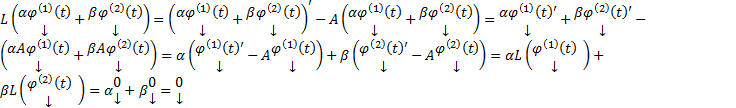 . Сейчас доказано, что L является линейным оператором и что любая ЛК решения также является решением.
. Сейчас доказано, что L является линейным оператором и что любая ЛК решения также является решением.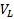
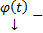 решение (1) или (3) с непрерывными коэффициентами
решение (1) или (3) с непрерывными коэффициентами 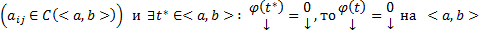
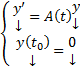 , но эта ЗК также обладает решением
, но эта ЗК также обладает решением 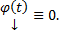
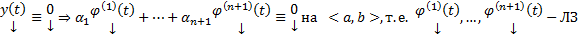
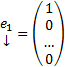 ,
, 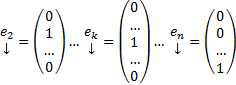 и рассмотрим n штук ЗК :
и рассмотрим n штук ЗК : 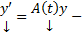 ОСЛОДУ
ОСЛОДУ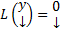
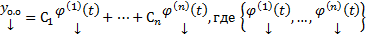 назовем ФСР ОСЛОДУ,
назовем ФСР ОСЛОДУ, 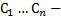 произвольные постоянные
произвольные постоянные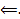 Поскольку
Поскольку 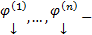 базис, то любое решение является ЛК
базис, то любое решение является ЛК 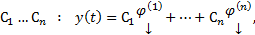
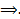 Из свойства линейности любая ЛК
Из свойства линейности любая ЛК 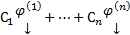 является решением.
является решением.


