Пусть 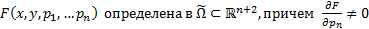
Опр. 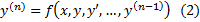 , где f определена в
, где f определена в 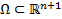 , то
, то
Опр. (2) называется ОДУ 1-го порядка, разрешенном относительно старшей производной
Опр. Частным решением уравнения (1) или (2) называется функция 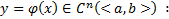
1) 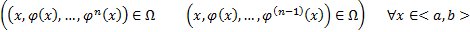
2) 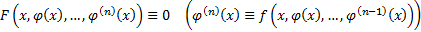 на
на 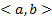
Совокупность всевозможных частных решений образует общее решение.
ЗК для (2) ставится следующим образом:
Нужно отыскать решения уравнения (2), удовлетворяющие дополнительному условию (называется начальными условиями)
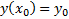
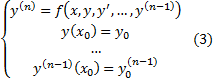
Теор. (ТСЕ решения ЗК (3) )
Если в некоторой области 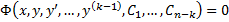 являющееся следствием уравнения (2), называется частным интегралом этого уравнения. Например, соотношение
являющееся следствием уравнения (2), называется частным интегралом этого уравнения. Например, соотношение 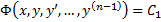 , является следствием уравнения (2), называется первым интегралом. Т.е. функция
, является следствием уравнения (2), называется первым интегралом. Т.е. функция 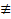 const, но сохраняет постоянное значение на любом решении уравнения (2)
const, но сохраняет постоянное значение на любом решении уравнения (2)





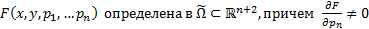
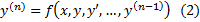 , где f определена в
, где f определена в 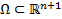 , то
, то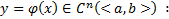
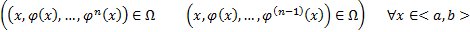
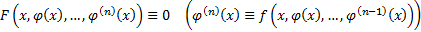 на
на 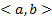
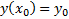
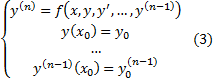
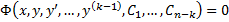 являющееся следствием уравнения (2), называется частным интегралом этого уравнения. Например, соотношение
являющееся следствием уравнения (2), называется частным интегралом этого уравнения. Например, соотношение 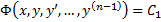 , является следствием уравнения (2), называется первым интегралом. Т.е. функция
, является следствием уравнения (2), называется первым интегралом. Т.е. функция 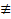 const, но сохраняет постоянное значение на любом решении уравнения (2)
const, но сохраняет постоянное значение на любом решении уравнения (2)


