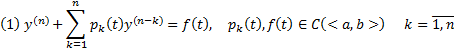
Теор. (Об общем решении НЛОДУ ВП)
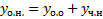
Док-во: Приведем (1) к виду (2) 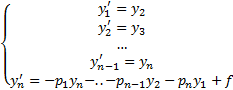
Пусть 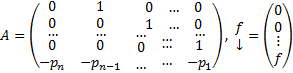
Получили неоднородное СЛОДУ 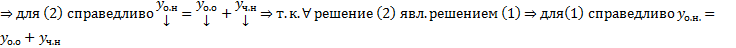 . Покажем, что
. Покажем, что 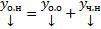 справедливо для (2).
справедливо для (2).
Покажем, что 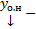 решение.
решение. 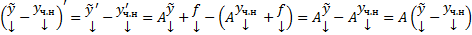 . Пусть
. Пусть 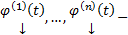 какая-нибудь ФСР ОСЛОДУ (2), тогда
какая-нибудь ФСР ОСЛОДУ (2), тогда 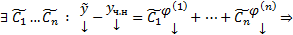 любое решение
любое решение  СЛОДУ (1) может быть представлено в виде
СЛОДУ (1) может быть представлено в виде 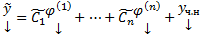 при некоторых значениях
при некоторых значениях 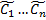
Вопрос 30.
Будем искать ч.н. методом вариации произвольных постоянных
Пусть 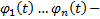 произвольная ФСР ОЛОДУ. Тогда
произвольная ФСР ОЛОДУ. Тогда 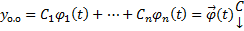 , где
, где 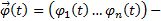 строка элементов ФСР,
строка элементов ФСР, 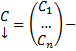 столбец произвольных постоянных.
столбец произвольных постоянных.
Будем искать 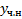 в виде
в виде 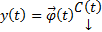 , где
, где 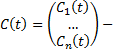 столбец неизвестных пока функций. Тогда
столбец неизвестных пока функций. Тогда 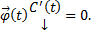 Тогда
Тогда 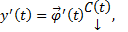
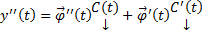 , наложим условия
, наложим условия 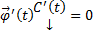 . Тогда
. Тогда 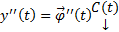 и т.д. На каждом шаге полагаем, что
и т.д. На каждом шаге полагаем, что 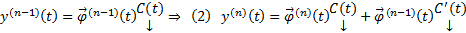 Поскольку
Поскольку 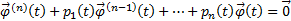 , тогда
, тогда 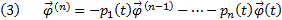 . С другой стороны, поскольку y является решением неоднородного уравнения (1), то
. С другой стороны, поскольку y является решением неоднородного уравнения (1), то 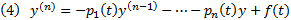 Подставим (3) и (4) в (2) получим :
Подставим (3) и (4) в (2) получим : 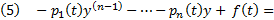 (
( 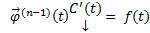 Следовательно, столбец
Следовательно, столбец 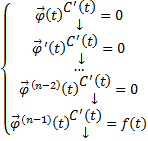 Запишем в развернутой форме
Запишем в развернутой форме 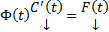 Поскольку
Поскольку 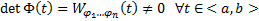 , то
, то 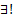 решение
решение 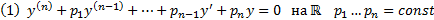
Рассмотрим ЛП 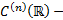 ЛП функций, непрерывные с производной до n-го порядка включительно на
ЛП функций, непрерывные с производной до n-го порядка включительно на 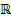 . Пусть в это ЛП действ ЛО
. Пусть в это ЛП действ ЛО 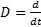 , т.е.
, т.е. 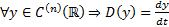
Далее получаем, что 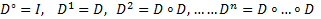
Тогда 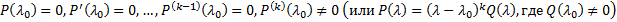 . Тогда
. Тогда 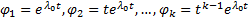 является решением ОЛОДУ ВП
является решением ОЛОДУ ВП 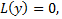 отвечающим значению
отвечающим значению 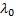
Перед доказательством этой теоремы рассмотрим.
Лемма. (Дифференциальное тождество)
Пусть 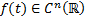 . Тогда
. Тогда 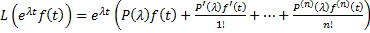
Док-во: Рассмотрим 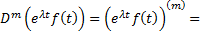 формула Лейбница
формула Лейбница 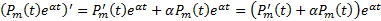 Если
Если 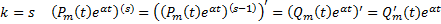 (см базу) – верно
(см базу) – верно 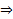 утверждение верно
утверждение верно 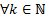 #
#
Пусть теперь характеристическое уравнение имеет корни : 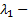 кратности
кратности 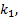
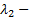 кратности
кратности 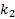 ,…,
,…, 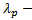 кратности
кратности 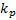
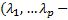 различны,
различны, 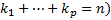 . Тогда рассмотрим сумму h функций (решений ОЛОДУ ВП)
. Тогда рассмотрим сумму h функций (решений ОЛОДУ ВП) 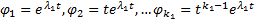

…
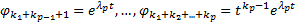 Покажем, что эта система ЛНЗ (тогда это и будет ФСР). От противного. Предположим, что она ЛЗ, что
Покажем, что эта система ЛНЗ (тогда это и будет ФСР). От противного. Предположим, что она ЛЗ, что 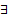 нетривиальный набор чисел
нетривиальный набор чисел 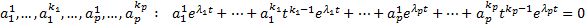 . Поскольку набор чисел нетривиальный, то хотя бы один из многочленов
. Поскольку набор чисел нетривиальный, то хотя бы один из многочленов 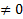 . БОО считаем, что
. БОО считаем, что 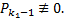 На самом деле, не только он, т.к если бы все остальные многочлены
На самом деле, не только он, т.к если бы все остальные многочлены 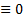 , то мы бы получили тождество :
, то мы бы получили тождество : 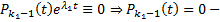 противоречие
противоречие 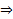 есть еще какой-то ненулевой многочлен. Тогда
есть еще какой-то ненулевой многочлен. Тогда 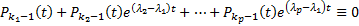 Дифференцируем это тождество k раз
Дифференцируем это тождество k раз 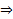 по лемме
по лемме 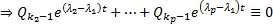 Какой-то многочлен из
Какой-то многочлен из 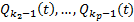 будет
будет 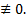 БОО это
БОО это  . По тем же соображениям, что и выше не только он
. По тем же соображениям, что и выше не только он 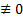 , но и еще по крайней мере один другой. Умножаем обе части на
, но и еще по крайней мере один другой. Умножаем обе части на 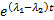 , получим
, получим 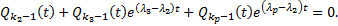 Дифференцируем еще
Дифференцируем еще 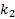 раз. Далее используем те же соображения дойдем до того, что
раз. Далее используем те же соображения дойдем до того, что 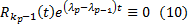 . С одной стороны из рассуждений, приведенных выше, получаем, что
. С одной стороны из рассуждений, приведенных выше, получаем, что  С другой стороны тождество (10) может быть выполнено только при
С другой стороны тождество (10) может быть выполнено только при 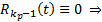 противоречие. Оно возникло из предположения, что
противоречие. Оно возникло из предположения, что 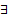 нетривиальная ЛК построенных функций, которое
нетривиальная ЛК построенных функций, которое 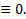 Значит, предположение неверно
Значит, предположение неверно 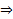 только тривиальная ЛК
только тривиальная ЛК 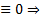 построеная система функций ЛНЗ
построеная система функций ЛНЗ 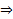 она представляет собой ФСР (вообще говоря
она представляет собой ФСР (вообще говоря 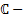 значную). Для уравнения с вещественными коэффициентами из нее можно построить вещественную ФСР по тем же правилам что и в случае простых костей. #
значную). Для уравнения с вещественными коэффициентами из нее можно построить вещественную ФСР по тем же правилам что и в случае простых костей. #





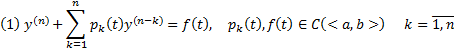
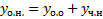
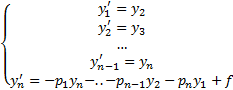
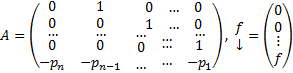
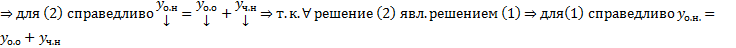 . Покажем, что
. Покажем, что 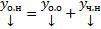 справедливо для (2).
справедливо для (2). 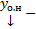 решение.
решение. 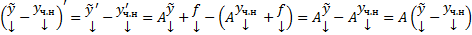 . Пусть
. Пусть 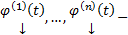 какая-нибудь ФСР ОСЛОДУ (2), тогда
какая-нибудь ФСР ОСЛОДУ (2), тогда 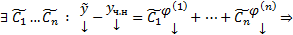 любое решение
любое решение  СЛОДУ (1) может быть представлено в виде
СЛОДУ (1) может быть представлено в виде 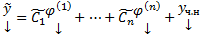 при некоторых значениях
при некоторых значениях 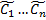
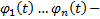 произвольная ФСР ОЛОДУ. Тогда
произвольная ФСР ОЛОДУ. Тогда 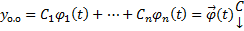 , где
, где 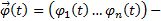 строка элементов ФСР,
строка элементов ФСР, 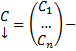 столбец произвольных постоянных.
столбец произвольных постоянных.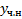 в виде
в виде 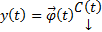 , где
, где 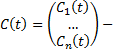 столбец неизвестных пока функций. Тогда
столбец неизвестных пока функций. Тогда 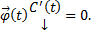 Тогда
Тогда 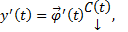
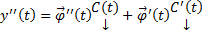 , наложим условия
, наложим условия 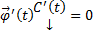 . Тогда
. Тогда 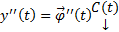 и т.д. На каждом шаге полагаем, что
и т.д. На каждом шаге полагаем, что 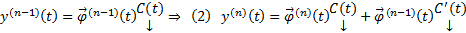 Поскольку
Поскольку 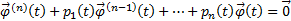 , тогда
, тогда 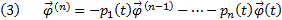 . С другой стороны, поскольку y является решением неоднородного уравнения (1), то
. С другой стороны, поскольку y является решением неоднородного уравнения (1), то 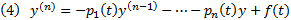 Подставим (3) и (4) в (2) получим :
Подставим (3) и (4) в (2) получим : 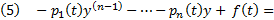 (
( 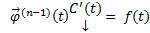 Следовательно, столбец
Следовательно, столбец 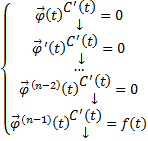 Запишем в развернутой форме
Запишем в развернутой форме 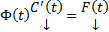 Поскольку
Поскольку 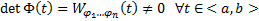 , то
, то 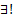 решение
решение 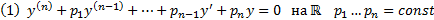
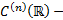 ЛП функций, непрерывные с производной до n-го порядка включительно на
ЛП функций, непрерывные с производной до n-го порядка включительно на 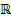 . Пусть в это ЛП действ ЛО
. Пусть в это ЛП действ ЛО 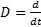 , т.е.
, т.е. 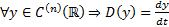
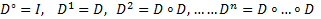
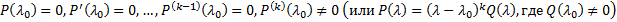 . Тогда
. Тогда 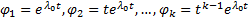 является решением ОЛОДУ ВП
является решением ОЛОДУ ВП 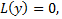 отвечающим значению
отвечающим значению 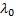
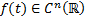 . Тогда
. Тогда 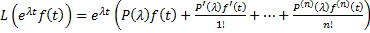
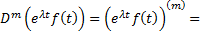 формула Лейбница
формула Лейбница 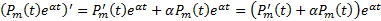 Если
Если 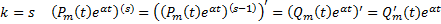 (см базу) – верно
(см базу) – верно 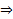 утверждение верно
утверждение верно 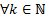 #
#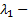 кратности
кратности 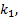
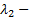 кратности
кратности 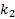 ,…,
,…, 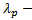 кратности
кратности 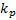
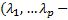 различны,
различны, 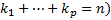 . Тогда рассмотрим сумму h функций (решений ОЛОДУ ВП)
. Тогда рассмотрим сумму h функций (решений ОЛОДУ ВП) 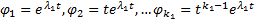

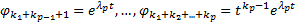 Покажем, что эта система ЛНЗ (тогда это и будет ФСР). От противного. Предположим, что она ЛЗ, что
Покажем, что эта система ЛНЗ (тогда это и будет ФСР). От противного. Предположим, что она ЛЗ, что 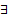 нетривиальный набор чисел
нетривиальный набор чисел 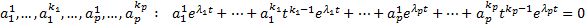 . Поскольку набор чисел нетривиальный, то хотя бы один из многочленов
. Поскольку набор чисел нетривиальный, то хотя бы один из многочленов 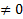 . БОО считаем, что
. БОО считаем, что 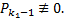 На самом деле, не только он, т.к если бы все остальные многочлены
На самом деле, не только он, т.к если бы все остальные многочлены 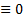 , то мы бы получили тождество :
, то мы бы получили тождество : 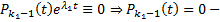 противоречие
противоречие 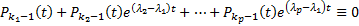 Дифференцируем это тождество k раз
Дифференцируем это тождество k раз 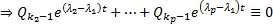 Какой-то многочлен из
Какой-то многочлен из 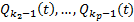 будет
будет 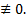 БОО это
БОО это  . По тем же соображениям, что и выше не только он
. По тем же соображениям, что и выше не только он 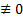 , но и еще по крайней мере один другой. Умножаем обе части на
, но и еще по крайней мере один другой. Умножаем обе части на 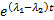 , получим
, получим 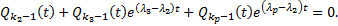 Дифференцируем еще
Дифференцируем еще 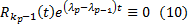 . С одной стороны из рассуждений, приведенных выше, получаем, что
. С одной стороны из рассуждений, приведенных выше, получаем, что  С другой стороны тождество (10) может быть выполнено только при
С другой стороны тождество (10) может быть выполнено только при 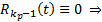 противоречие. Оно возникло из предположения, что
противоречие. Оно возникло из предположения, что 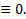 Значит, предположение неверно
Значит, предположение неверно 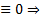 построеная система функций ЛНЗ
построеная система функций ЛНЗ 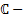 значную). Для уравнения с вещественными коэффициентами из нее можно построить вещественную ФСР по тем же правилам что и в случае простых костей. #
значную). Для уравнения с вещественными коэффициентами из нее можно построить вещественную ФСР по тем же правилам что и в случае простых костей. #


