

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Оснащения врачебно-сестринской бригады.
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Интересное:
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
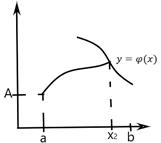
Ставится задача нахождения экстремума функционала 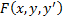 непрерывна с элементами до 2-го порядка включительно
непрерывна с элементами до 2-го порядка включительно
2) 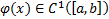 , тогда
, тогда
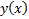 является решением уравнения Эйлера для функционала (1) :
является решением уравнения Эйлера для функционала (1) : 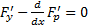 , удовлетворяющим условиям (2), (3) и кроме того, на правом конце для него выполняется условие транверсальности :
, удовлетворяющим условиям (2), (3) и кроме того, на правом конце для него выполняется условие транверсальности : 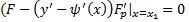
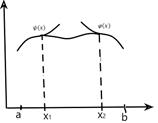
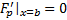
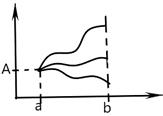
Пример 1. Найти условие трансверсальности для функционала 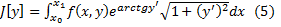
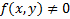
Решение. Пусть левый конец экстремали закреплен в точке 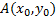 , а правый конец
, а правый конец 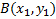 может перемещаться по кривой
может перемещаться по кривой 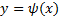 . Тогда получим
. Тогда получим 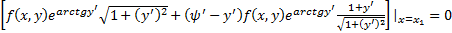 . Отсюда в силу условия
. Отсюда в силу условия 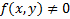 , получаем
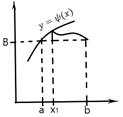
, получаем 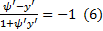 . Геометрически условие(6) означает, что экстремали
. Геометрически условие(6) означает, что экстремали 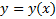 должны пересекать кривую
должны пересекать кривую 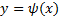 , по которой скользит граничная точка
, по которой скользит граничная точка 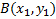 по углом
по углом  .
.
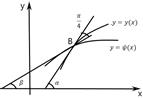 В самом деле, соотношение (6) можно представить так: положим, что касательная к экстремали в точке
В самом деле, соотношение (6) можно представить так: положим, что касательная к экстремали в точке 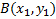 , лежащей на кривой
, лежащей на кривой 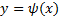 , пересекает ось Ox под углом
, пересекает ось Ox под углом 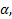 а касательная к заданной кривой
а касательная к заданной кривой 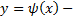 под углом
под углом 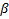 . Тогда
. Тогда 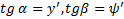 и левая часть формулы (6) дает
и левая часть формулы (6) дает 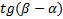 , но
, но 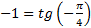 , поэтому
, поэтому 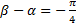 , откуда
, откуда 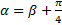 , откуда
, откуда 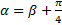 , что и требовалось показать.
, что и требовалось показать.
Пример 2.Найти минимальное расстояние между параболой 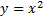 и прямой
и прямой 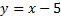
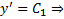 условие трансверсальности приобретает следующий вид :
условие трансверсальности приобретает следующий вид : 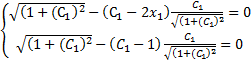
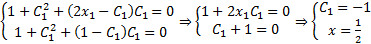 . Теперь используем граничные условия
. Теперь используем граничные условия 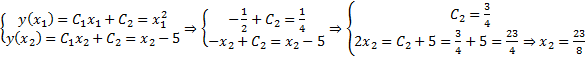
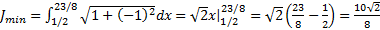
|
|
|

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
© cyberpedia.su 2017-2026 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!