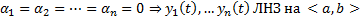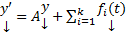
ДОКАЗАТЬ
Метод неопределенных коэффициентов.
Теор. Если 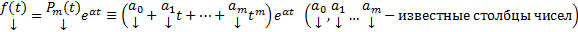 ,
,
то 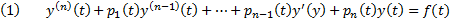
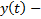 неизвестная функция
неизвестная функция
(1) Называется ЛОДУ ВП, 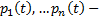 его коэффициенты
его коэффициенты
Будем считать, что 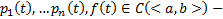 непрерывны на рассмотренном интервале
непрерывны на рассмотренном интервале
Если 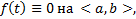 то ЛОДУ ВП называется однородным, в противном случае – неоднородным (противоположный случай, когда f хотя бы в одной точке отлична от 0)
то ЛОДУ ВП называется однородным, в противном случае – неоднородным (противоположный случай, когда f хотя бы в одной точке отлична от 0)
Опр. 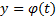 называется частным решением (1), если
называется частным решением (1), если 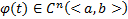 и при подстановке в (1) обращает его в тождество
и при подстановке в (1) обращает его в тождество
Опр. Совокупность всевозможных частных решений образует общее решение уравнения (1). Сведем (1) к нормальной системе
Пусть 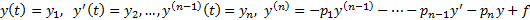
Тогда (2) 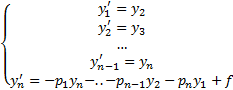
Всякое решение (1) будет решением (2) и наоборот. Поэтому (1) эквивалентна системе (2) и соответственно его общее решение содержат и произвольных постоянных. Пусть 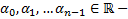 произвольный набор чисел ЗК для (1) формулируется следующим образом: найти решение уравнения (1), удовлетворяющее дополнительным условиям (3)
произвольный набор чисел ЗК для (1) формулируется следующим образом: найти решение уравнения (1), удовлетворяющее дополнительным условиям (3) 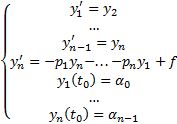
В данном случае 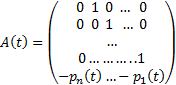 ,
, 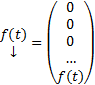 Из связи ЗК (2) (3) с ЗК для СЛОДУ с непрерывными коэффициентами
Из связи ЗК (2) (3) с ЗК для СЛОДУ с непрерывными коэффициентами 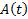 и
и 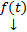 получаем:
получаем:
Теор. (ТСЕ)
Если 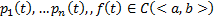 , то для
, то для 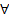 набора
набора 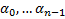 на всем
на всем 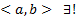 решение ЗК (1), (2) теорема носит глобальный характер
решение ЗК (1), (2) теорема носит глобальный характер
Вопрос 25
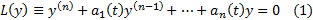
Опр. Функции 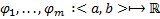 называются ЛЗ на
называются ЛЗ на 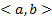 , если существуют вещественные числа, не все равнее нулю, такие, что при всех
, если существуют вещественные числа, не все равнее нулю, такие, что при всех 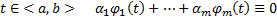 . В противном случае функции
. В противном случае функции 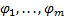 называются ЛНЗ на
называются ЛНЗ на 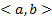
Утв. Любые (n+1) решений уравнения (1) ЛЗ на 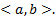
Док-во: Пусть 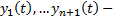 решения уравнения (1) на
решения уравнения (1) на 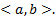 Составим их линейную комбинацию и приравняем ее к нулю
Составим их линейную комбинацию и приравняем ее к нулю 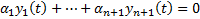 . Последовательно дифференцируем это равенство (n-1) раз. В результате получим следующую систему n уравнений
. Последовательно дифференцируем это равенство (n-1) раз. В результате получим следующую систему n уравнений 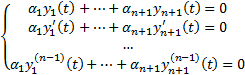 Зафиксируем
Зафиксируем 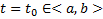 в этой системе уравнений.
в этой системе уравнений. 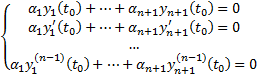 Относительно переменных
Относительно переменных 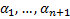 это однородная система линейных алгебраических уравнений, у которой число уравнений (n) меньше числа неизвестных (n+1), поэтому она имеет бесконечное множество нетривиальных решений. Пусть
это однородная система линейных алгебраических уравнений, у которой число уравнений (n) меньше числа неизвестных (n+1), поэтому она имеет бесконечное множество нетривиальных решений. Пусть 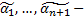 одно из них. Рассмотрим функцию
одно из них. Рассмотрим функцию 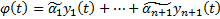 . Эта функция является решением уравнения (1). Кроме того,
. Эта функция является решением уравнения (1). Кроме того, 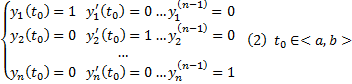 . Покажем, что они ЛНЗ.
. Покажем, что они ЛНЗ. 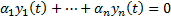 Последовательно дифференцируем это равенство n-1 раз
Последовательно дифференцируем это равенство n-1 раз 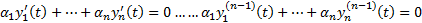 . Положим
. Положим 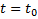 . С учетом начальных условий (2) получаем
. С учетом начальных условий (2) получаем 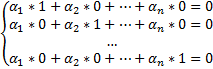 Отсюда
Отсюда 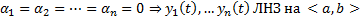





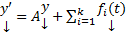
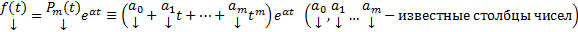 ,
,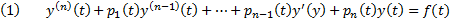
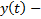 неизвестная функция
неизвестная функция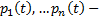 его коэффициенты
его коэффициенты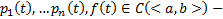 непрерывны на рассмотренном интервале
непрерывны на рассмотренном интервале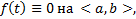 то ЛОДУ ВП называется однородным, в противном случае – неоднородным (противоположный случай, когда f хотя бы в одной точке отлична от 0)
то ЛОДУ ВП называется однородным, в противном случае – неоднородным (противоположный случай, когда f хотя бы в одной точке отлична от 0)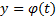 называется частным решением (1), если
называется частным решением (1), если 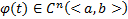 и при подстановке в (1) обращает его в тождество
и при подстановке в (1) обращает его в тождество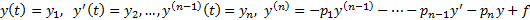
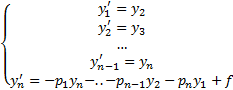
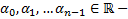 произвольный набор чисел ЗК для (1) формулируется следующим образом: найти решение уравнения (1), удовлетворяющее дополнительным условиям (3)
произвольный набор чисел ЗК для (1) формулируется следующим образом: найти решение уравнения (1), удовлетворяющее дополнительным условиям (3) 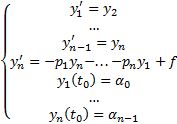
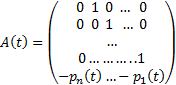 ,
, 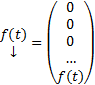 Из связи ЗК (2) (3) с ЗК для СЛОДУ с непрерывными коэффициентами
Из связи ЗК (2) (3) с ЗК для СЛОДУ с непрерывными коэффициентами 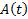 и
и 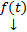 получаем:
получаем: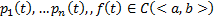 , то для
, то для 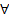 набора
набора 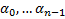 на всем
на всем 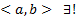 решение ЗК (1), (2) теорема носит глобальный характер
решение ЗК (1), (2) теорема носит глобальный характер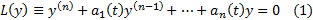
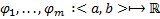 называются ЛЗ на
называются ЛЗ на 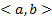 , если существуют вещественные числа, не все равнее нулю, такие, что при всех
, если существуют вещественные числа, не все равнее нулю, такие, что при всех 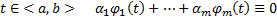 . В противном случае функции
. В противном случае функции 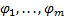 называются ЛНЗ на
называются ЛНЗ на 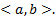
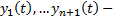 решения уравнения (1) на
решения уравнения (1) на 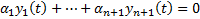 . Последовательно дифференцируем это равенство (n-1) раз. В результате получим следующую систему n уравнений
. Последовательно дифференцируем это равенство (n-1) раз. В результате получим следующую систему n уравнений 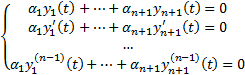 Зафиксируем
Зафиксируем 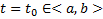 в этой системе уравнений.
в этой системе уравнений. 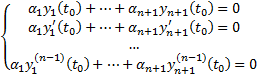 Относительно переменных
Относительно переменных 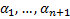 это однородная система линейных алгебраических уравнений, у которой число уравнений (n) меньше числа неизвестных (n+1), поэтому она имеет бесконечное множество нетривиальных решений. Пусть
это однородная система линейных алгебраических уравнений, у которой число уравнений (n) меньше числа неизвестных (n+1), поэтому она имеет бесконечное множество нетривиальных решений. Пусть 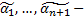 одно из них. Рассмотрим функцию
одно из них. Рассмотрим функцию 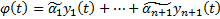 . Эта функция является решением уравнения (1). Кроме того,
. Эта функция является решением уравнения (1). Кроме того, 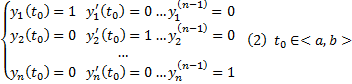 . Покажем, что они ЛНЗ.
. Покажем, что они ЛНЗ. 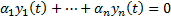 Последовательно дифференцируем это равенство n-1 раз
Последовательно дифференцируем это равенство n-1 раз 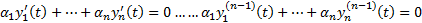 . Положим
. Положим 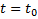 . С учетом начальных условий (2) получаем
. С учетом начальных условий (2) получаем 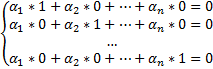 Отсюда
Отсюда