А) Простейшее уравнение n -го порядка
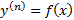 , где
, где 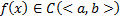 . Проинтегрировав это уравнение по x
. Проинтегрировав это уравнение по x 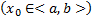
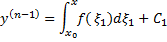
Далее 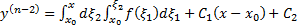
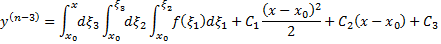
Через некоторое количество шагов
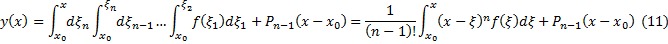
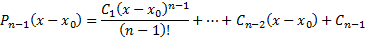
Док-во: Докажем (11) методом математической индукции.
БАЗА. 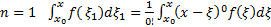 (верно)
(верно)
ШАГ. Пусть утверждение верно для 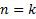 , т.е.
, т.е. 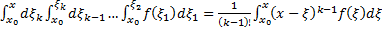 .
.
Тогда 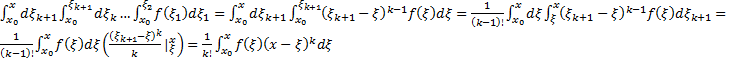 , т.е. формула верна и для
, т.е. формула верна и для 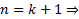 утверждение верно.
утверждение верно.
Таким образом, простейшее уравнение n-го порядка всегда интегрируемо в квадратурах имеет вид (11) #
Теперь докажем, что 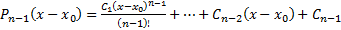
Док-во: Применим метод ММИ. БАЗА 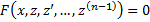 . Допустим, что решение
. Допустим, что решение 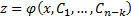 . Тогда полученный промежуточный интеграл
. Тогда полученный промежуточный интеграл 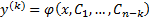
б) 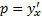 . Если
. Если 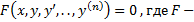 однородное, то аргумент
однородное, то аргумент 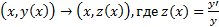 .
.
В этом случае 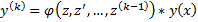
БАЗА для 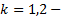 верно(см.выше)
верно(см.выше)
ШАГ индукции. Допустим, что утверждение верно для 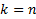 , докажем что оно также верно для
, докажем что оно также верно для 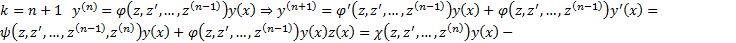 верно , то есть утверждение справедливо
верно , то есть утверждение справедливо 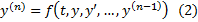 можно свести к нормальной системе следующим образом:
можно свести к нормальной системе следующим образом:
Пусть 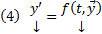 . Тогда частное решение (4) это вектор столбец
. Тогда частное решение (4) это вектор столбец 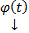 (или вектор строка
(или вектор строка 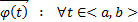
1) 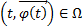
2) 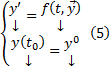 Подразумевается, что
Подразумевается, что 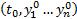 является внутренней точкой
является внутренней точкой 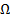
Теор.(ТСЕ)
Пусть 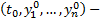 внутренняя точка
внутренняя точка 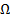 и в некоторой
и в некоторой 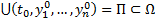
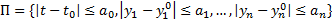 выполняется, что
выполняется, что
1) 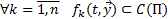
2) 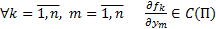 Тогда
Тогда 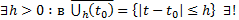 решение ЗК (5)
решение ЗК (5)
Замеч. Если 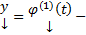 решение ЗК (5) на
решение ЗК (5) на 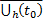 , а
, а 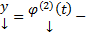 решение ЗК (5) на некотором D, то
решение ЗК (5) на некотором D, то 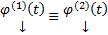 на
на 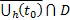
Линейные нормальные системы.
Рассмотрим (1) 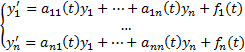 Будем считать, что
Будем считать, что 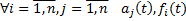 определены и непрерывны на
определены и непрерывны на 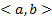
Опр. (1) называется линейной нормальной(СЛОДУ) системой (ОДУ 1-го порядка) (сама система имеет порядок n)
Введя обозначение 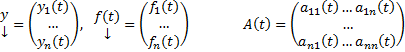 перепишем (1) в виде
перепишем (1) в виде 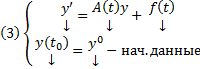
Теор.(ТСЕ для СЛОДУ)
Если 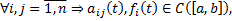 то на всем
то на всем 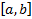 при любом наборе начальных данных
при любом наборе начальных данных 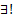 решение ЗК (3) на всем
решение ЗК (3) на всем 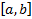
Без доказательства





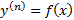 , где
, где 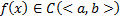 . Проинтегрировав это уравнение по x
. Проинтегрировав это уравнение по x 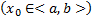
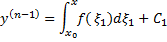
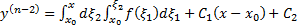
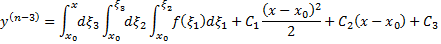
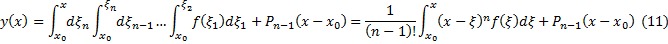
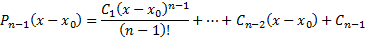
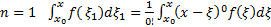 (верно)
(верно)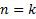 , т.е.
, т.е. 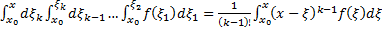 .
.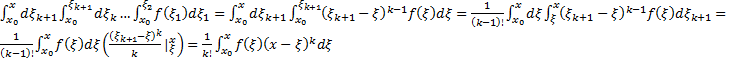 , т.е. формула верна и для
, т.е. формула верна и для 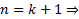 утверждение верно.
утверждение верно.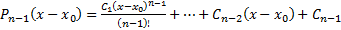
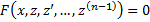 . Допустим, что решение
. Допустим, что решение 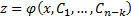 . Тогда полученный промежуточный интеграл
. Тогда полученный промежуточный интеграл 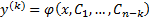
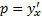 . Если
. Если 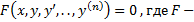 однородное, то аргумент
однородное, то аргумент 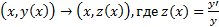 .
.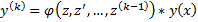
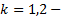 верно(см.выше)
верно(см.выше)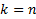 , докажем что оно также верно для
, докажем что оно также верно для 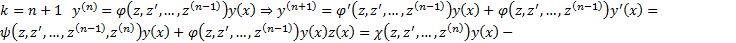 верно , то есть утверждение справедливо
верно , то есть утверждение справедливо 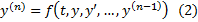 можно свести к нормальной системе следующим образом:
можно свести к нормальной системе следующим образом: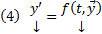 . Тогда частное решение (4) это вектор столбец
. Тогда частное решение (4) это вектор столбец 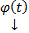 (или вектор строка
(или вектор строка 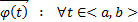
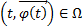
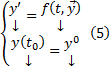 Подразумевается, что
Подразумевается, что 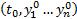 является внутренней точкой
является внутренней точкой 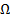
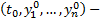 внутренняя точка
внутренняя точка 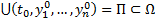
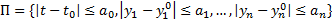 выполняется, что
выполняется, что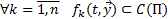
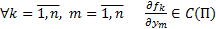 Тогда
Тогда 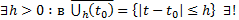 решение ЗК (5)
решение ЗК (5)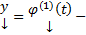 решение ЗК (5) на
решение ЗК (5) на 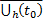 , а
, а 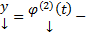 решение ЗК (5) на некотором D, то
решение ЗК (5) на некотором D, то 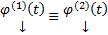 на
на 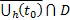
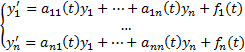 Будем считать, что
Будем считать, что 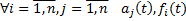 определены и непрерывны на
определены и непрерывны на 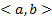
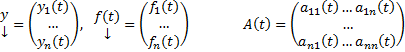 перепишем (1) в виде
перепишем (1) в виде 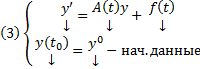
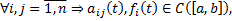 то на всем
то на всем 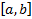 при любом наборе начальных данных
при любом наборе начальных данных 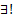 решение ЗК (3) на всем
решение ЗК (3) на всем 

