Вопрос 28. Формула Лиувилля. Произвольная система ЛЗ функций

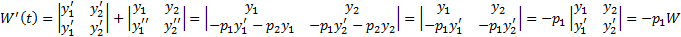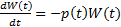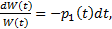
(1) , т.е. получаем ОДУ , 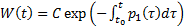При 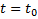 получим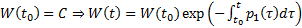

Сл. Если 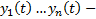решение ЛОДУ ВП (1) (с непрерывными коэффициентами на 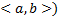, то либо 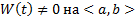, либо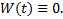

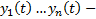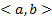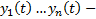7) Если решение ЛОДУ ВП (1) с непрерывными коэффициентами на  и в некоторой , то ЛЗ на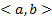

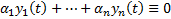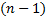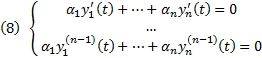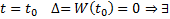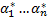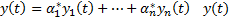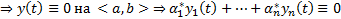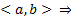Док-во: Пусть . Дифференцируем  раз, получим   При  нетривиальное решение . Рассмотрим  является решением ЗК для (1) с нетривиальным НУ. Эта ЗК также имеет тривиальное решение  на   ЛЗ

Замеч. Это свойство не выполняется для произв (n-1) раз дифф функций на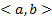

8) Свойство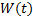

Если 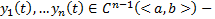произвольная система ЛЗ функций на 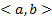, то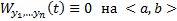

Док-во: Пусть 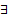нетривиальный набор 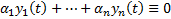. Тогда 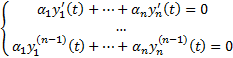Поскольку 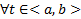эта СЛАУ обладает нетривиальным решением, то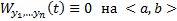

9) (О построении уравнения по ФСР)

Система функций 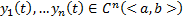 образует ФСР некоторого ЛОДУ n-го порядка с непрерывными на  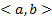коэффициентами

Док-во: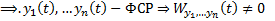

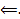Пусть теперь 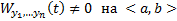. Рассмотрим 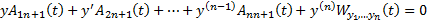. Соотв алгебраические коэффициенты выражены через известные функции и  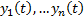и их производные до n порядка включительно  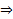определены и непрерывны на 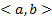. Тогда  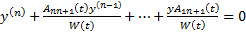Получим искомое уравнение, примем  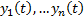его ФСР.

10) Есл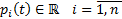и  и 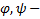вещественные функции  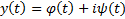является комплексным решением уравнения . Тогда 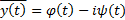 также является решением и  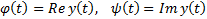также является решением