Пусть 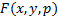 определена в
определена в 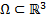 . Рассмотрим уравнение
. Рассмотрим уравнение 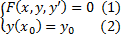
1) 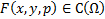
2) 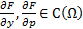
3) 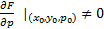 тогда в некоторой
тогда в некоторой 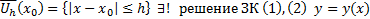 , причем дополнительно выполнено условие
, причем дополнительно выполнено условие 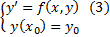 , причем
, причем 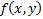 непрерывна и
непрерывна и 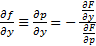 непрерывна в окрестности точки
непрерывна в окрестности точки 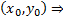 выполняется условие ТСЕ решения ЗК для уравнения 1-го порядка, разрешенного относительно производной
выполняется условие ТСЕ решения ЗК для уравнения 1-го порядка, разрешенного относительно производной
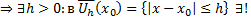 решение ЗК (3), которое является и единственным решением ЗК (1), (2) удовлетворяющее дополнительному условию
решение ЗК (3), которое является и единственным решением ЗК (1), (2) удовлетворяющее дополнительному условию 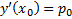 необходима для того, чтобы из множества интегральных кривых, проходящий через
необходима для того, чтобы из множества интегральных кривых, проходящий через 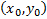 выбрать кривую единственную проходящую по направлению
выбрать кривую единственную проходящую по направлению 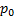
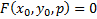 может иметь несколько решений
может иметь несколько решений 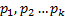
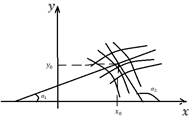 Рисунок для случая, когда имеется
Рисунок для случая, когда имеется 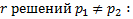
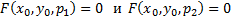 . Каждая из ЗК
. Каждая из ЗК 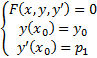
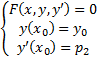 имеет единственное решение
имеет единственное решение

Замеч. Нарушение 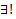 решение ЗК, проходящего по заданному направлению чаще всего связанно с нарушением 3 свойства ТСЕ, т.е. если
решение ЗК, проходящего по заданному направлению чаще всего связанно с нарушением 3 свойства ТСЕ, т.е. если 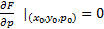 . В этом случае ЗК может не иметь решения, а может и иметь, причем возможно неединственное, проходящее по этому направлению
. В этом случае ЗК может не иметь решения, а может и иметь, причем возможно неединственное, проходящее по этому направлению 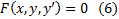
Известно, что уравнение 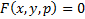 задает некоторую поверхность в
задает некоторую поверхность в 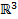 . Эта поверхность может быть параметризована следующим образом
. Эта поверхность может быть параметризована следующим образом 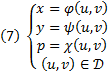 причем для
причем для 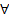
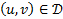 выполняется
выполняется 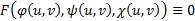 . На каждом решении уравнения (6) должно быть выполнено соотношение
. На каждом решении уравнения (6) должно быть выполнено соотношение 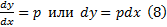 . Из (7) и (8) получаем , что
. Из (7) и (8) получаем , что 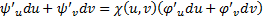
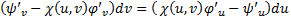
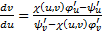 а это уравнение для
а это уравнение для 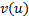 , разрешенное относительно производной
, разрешенное относительно производной
Пусть его общее решение имеет вид : 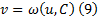 т.е. на всякой интегральной кривой
т.е. на всякой интегральной кривой 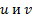 связаны соотношением (9) при некотором значении С. Тогда общее решение исходного уравнения может быть параметрически задано следующим образом
связаны соотношением (9) при некотором значении С. Тогда общее решение исходного уравнения может быть параметрически задано следующим образом 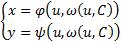
Частный случай
Если уравнение (6) легко разрешить относительно 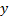 т.е. представить в виде
т.е. представить в виде 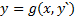 , то в качестве параметров выбирают
, то в качестве параметров выбирают 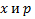 по следующей схеме
по следующей схеме 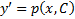 и интегр его, т.к. р – параметр
и интегр его, т.к. р – параметр
Рассмотрим 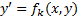 и решить их, объединить все решения.Поскольку далеко не всегда удается это сделать , чаще применяется метод введения параметра.
и решить их, объединить все решения.Поскольку далеко не всегда удается это сделать , чаще применяется метод введения параметра.





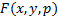 определена в
определена в 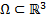 . Рассмотрим уравнение
. Рассмотрим уравнение 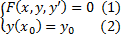
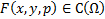
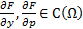
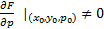 тогда в некоторой
тогда в некоторой 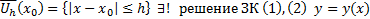 , причем дополнительно выполнено условие
, причем дополнительно выполнено условие 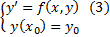 , причем
, причем 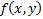 непрерывна и
непрерывна и 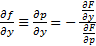 непрерывна в окрестности точки
непрерывна в окрестности точки 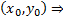 выполняется условие ТСЕ решения ЗК для уравнения 1-го порядка, разрешенного относительно производной
выполняется условие ТСЕ решения ЗК для уравнения 1-го порядка, разрешенного относительно производной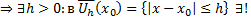 решение ЗК (3), которое является и единственным решением ЗК (1), (2) удовлетворяющее дополнительному условию
решение ЗК (3), которое является и единственным решением ЗК (1), (2) удовлетворяющее дополнительному условию 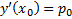 необходима для того, чтобы из множества интегральных кривых, проходящий через
необходима для того, чтобы из множества интегральных кривых, проходящий через 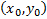 выбрать кривую единственную проходящую по направлению
выбрать кривую единственную проходящую по направлению 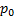
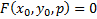 может иметь несколько решений
может иметь несколько решений 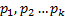
 Рисунок для случая, когда имеется
Рисунок для случая, когда имеется 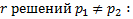
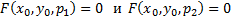 . Каждая из ЗК
. Каждая из ЗК 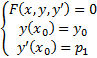
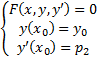 имеет единственное решение
имеет единственное решение
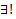 решение ЗК, проходящего по заданному направлению чаще всего связанно с нарушением 3 свойства ТСЕ, т.е. если
решение ЗК, проходящего по заданному направлению чаще всего связанно с нарушением 3 свойства ТСЕ, т.е. если 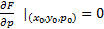 . В этом случае ЗК может не иметь решения, а может и иметь, причем возможно неединственное, проходящее по этому направлению
. В этом случае ЗК может не иметь решения, а может и иметь, причем возможно неединственное, проходящее по этому направлению 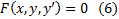
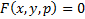 задает некоторую поверхность в
задает некоторую поверхность в 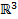 . Эта поверхность может быть параметризована следующим образом
. Эта поверхность может быть параметризована следующим образом 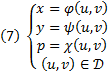 причем для
причем для 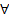
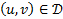 выполняется
выполняется 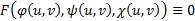 . На каждом решении уравнения (6) должно быть выполнено соотношение
. На каждом решении уравнения (6) должно быть выполнено соотношение 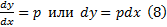 . Из (7) и (8) получаем , что
. Из (7) и (8) получаем , что 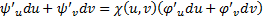
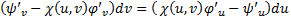
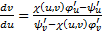 а это уравнение для
а это уравнение для 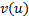 , разрешенное относительно производной
, разрешенное относительно производной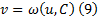 т.е. на всякой интегральной кривой
т.е. на всякой интегральной кривой 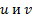 связаны соотношением (9) при некотором значении С. Тогда общее решение исходного уравнения может быть параметрически задано следующим образом
связаны соотношением (9) при некотором значении С. Тогда общее решение исходного уравнения может быть параметрически задано следующим образом 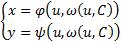
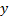 т.е. представить в виде
т.е. представить в виде 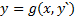 , то в качестве параметров выбирают
, то в качестве параметров выбирают 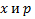 по следующей схеме
по следующей схеме 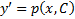 и интегр его, т.к. р – параметр
и интегр его, т.к. р – параметр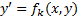 и решить их, объединить все решения.Поскольку далеко не всегда удается это сделать , чаще применяется метод введения параметра.
и решить их, объединить все решения.Поскольку далеко не всегда удается это сделать , чаще применяется метод введения параметра.


