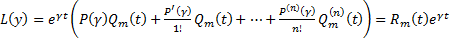 . Тогда
. Тогда 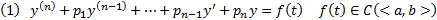
Напомним, что 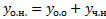
В случае произвольной 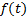 ищем
ищем 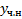 методом вариации произвольных постоянных. Однако в случае специального вида
методом вариации произвольных постоянных. Однако в случае специального вида 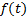 удобнее применять метод неопределенных коэффициентов
удобнее применять метод неопределенных коэффициентов
Теор. (принцип суперпозиции)
Если 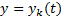 является решением уравнения
является решением уравнения 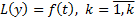 , то
, то 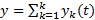 является решением уравнения
является решением уравнения 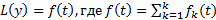
Док-во: 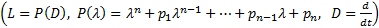
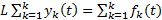 #
#
Пусть 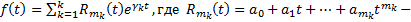 многочлен степени
многочлен степени 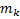 с определенными коэффициентами,
с определенными коэффициентами, 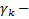 произвольная(комплексная)
произвольная(комплексная)
В силу принципа суперпозиции рассмотрим поиск 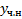 для
для 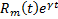
Возможны 2 случая :
1) 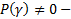 нерезонансный случай
нерезонансный случай
2) 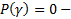 резонансный случай
резонансный случай
Резонансный случай.
Пусть 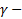 корень характеристического уравнения кратности k :
корень характеристического уравнения кратности k :  определена в
определена в 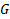
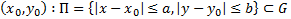
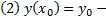 начальные условия
начальные условия
ЗК. Найти интегральную кривую уравнения (1) проходящую через 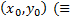 найти решение (1), удовлетворяющее н.у. (2))
найти решение (1), удовлетворяющее н.у. (2))
Теор. Пусть 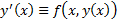 . Проинтегрируем это тождество от
. Проинтегрируем это тождество от 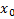 до
до 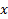
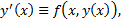 причем
причем 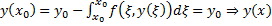 является решением ЗК (1), (2)##
является решением ЗК (1), (2)##
3) (Построение функциональной последовательности) Строим функциональную последовательность следующим образом. Везде считаем, что 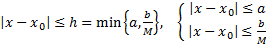
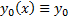
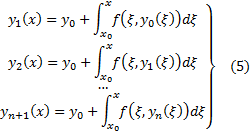
4) (Принадлежность П)
Покажем, что при 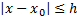 выполняется, что
выполняется, что 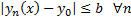 т.е.
т.е. 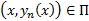
## 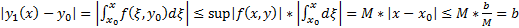
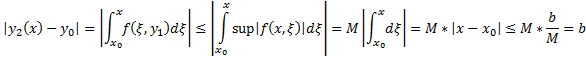
……
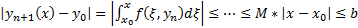 ##
##
5) (Абсолютная и равномерная сходимость функциональной последовательности)
Покажем, что 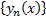 сходится абсолютно и равномерно на
сходится абсолютно и равномерно на 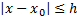
## Очевидно 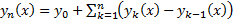 Таким образом, сходимость последовательности
Таким образом, сходимость последовательности 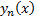 эквивалента сходимости функционального ряда
эквивалента сходимости функционального ряда 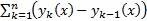 (т.к.
(т.к. 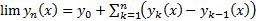
Рассмотрим 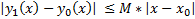 . Тогда
. Тогда 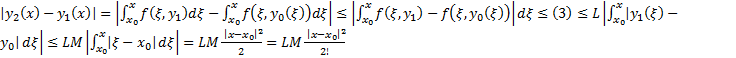
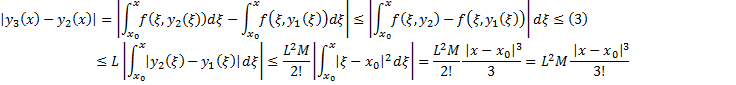
……
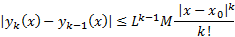
Тогда 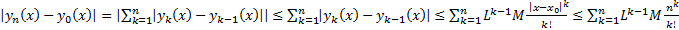 Числовой ряд
Числовой ряд 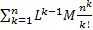 Сходится по признаку Даламбера
Сходится по признаку Даламбера 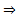
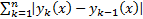 мажорируется сход числовым рядом
мажорируется сход числовым рядом 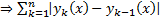 сходится абсолютно и равномерно на
сходится абсолютно и равномерно на 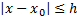 по правилу Вейерштрассе.
по правилу Вейерштрассе. 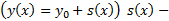 сумма ряда.
сумма ряда. 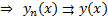 причем
причем 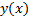 непрерывна при
непрерывна при 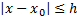 в случае равномерной сходимости.
в случае равномерной сходимости.
Замеч. 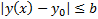 в силу теоремы о предельном преходе в неравенствах
в силу теоремы о предельном преходе в неравенствах
6) (Равномерная сходимость 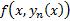 )
)
Покажем, что 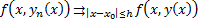
## 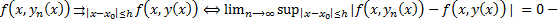 критерий сходимости функциональной последовательности. Рассмотрим
критерий сходимости функциональной последовательности. Рассмотрим  ##
##
7) (Решение интегрального уравнения)
Покажем, что 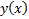 является решением интегрального уравнения (4)
является решением интегрального уравнения (4)
## 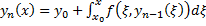 (из (5))
(из (5)) 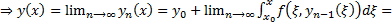 в силу равномерной сходимости
в силу равномерной сходимости 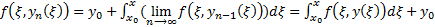 Но поскольку интегрируемое уравнение (4) эквивалентно ЗК (1), (2) то
Но поскольку интегрируемое уравнение (4) эквивалентно ЗК (1), (2) то 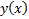 и является решенной ЗК ##
и является решенной ЗК ##
Таким образом доказано, что решение ЗК 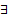
Доказательство конструктивное. Указан метод построения решения. (Метод последовательного приближения 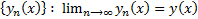 #
#





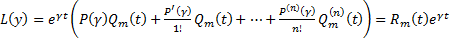 . Тогда
. Тогда 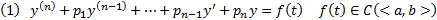
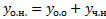
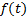 ищем
ищем 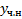 методом вариации произвольных постоянных. Однако в случае специального вида
методом вариации произвольных постоянных. Однако в случае специального вида 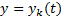 является решением уравнения
является решением уравнения 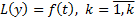 , то
, то 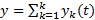 является решением уравнения
является решением уравнения 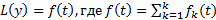
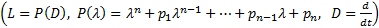
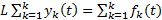 #
#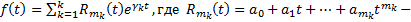 многочлен степени
многочлен степени 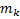 с определенными коэффициентами,
с определенными коэффициентами, 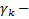 произвольная(комплексная)
произвольная(комплексная)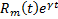
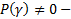 нерезонансный случай
нерезонансный случай 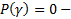 резонансный случай
резонансный случай 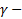 корень характеристического уравнения кратности k :
корень характеристического уравнения кратности k :  определена в
определена в 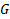
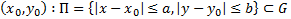
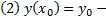 начальные условия
начальные условия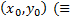 найти решение (1), удовлетворяющее н.у. (2))
найти решение (1), удовлетворяющее н.у. (2))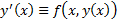 . Проинтегрируем это тождество от
. Проинтегрируем это тождество от 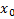 до
до 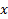
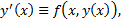 причем
причем 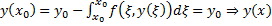 является решением ЗК (1), (2)##
является решением ЗК (1), (2)##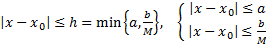
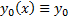
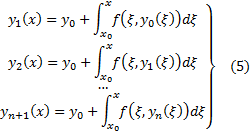
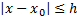 выполняется, что
выполняется, что 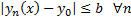 т.е.
т.е. 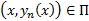
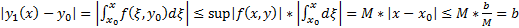
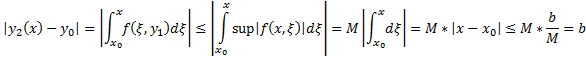
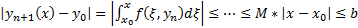 ##
##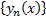 сходится абсолютно и равномерно на
сходится абсолютно и равномерно на 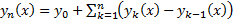 Таким образом, сходимость последовательности
Таким образом, сходимость последовательности 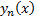 эквивалента сходимости функционального ряда
эквивалента сходимости функционального ряда 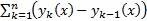 (т.к.
(т.к. 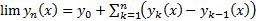
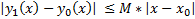 . Тогда
. Тогда 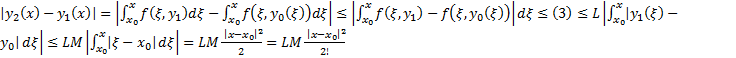
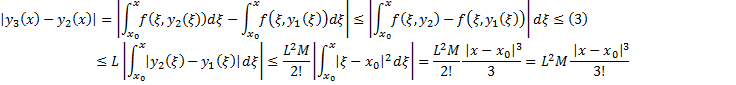
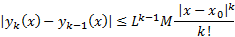
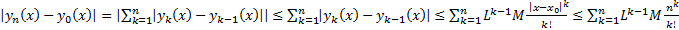 Числовой ряд
Числовой ряд 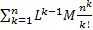 Сходится по признаку Даламбера
Сходится по признаку Даламбера 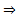
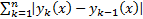 мажорируется сход числовым рядом
мажорируется сход числовым рядом 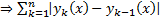 сходится абсолютно и равномерно на
сходится абсолютно и равномерно на 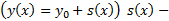 сумма ряда.
сумма ряда. 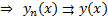 причем
причем 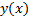 непрерывна при
непрерывна при 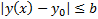 в силу теоремы о предельном преходе в неравенствах
в силу теоремы о предельном преходе в неравенствах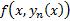 )
) 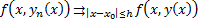
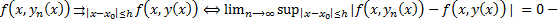 критерий сходимости функциональной последовательности. Рассмотрим
критерий сходимости функциональной последовательности. Рассмотрим  ##
##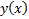 является решением интегрального уравнения (4)
является решением интегрального уравнения (4)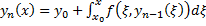 (из (5))
(из (5)) 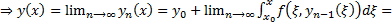 в силу равномерной сходимости
в силу равномерной сходимости 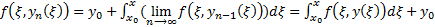 Но поскольку интегрируемое уравнение (4) эквивалентно ЗК (1), (2) то
Но поскольку интегрируемое уравнение (4) эквивалентно ЗК (1), (2) то 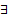
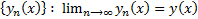 #
#


