Лемма. (Лемма Гронуолла)
Если 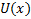 непрерывна и неотрицательна на
непрерывна и неотрицательна на 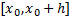 и удовлетворяет условию
и удовлетворяет условию 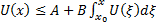 , то
, то 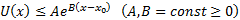
Док-во: рассмотрим 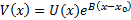 , которая также непрерывна и неотрицательна на
, которая также непрерывна и неотрицательна на 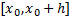
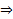 достигает своей верхней грани на
достигает своей верхней грани на 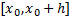 . Предположим, что
. Предположим, что 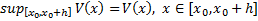
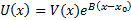
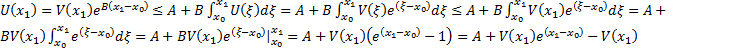
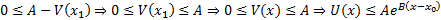 #
#
Докажем теперь единственность решения ЗК на 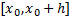 (слева доказывается аналогично)
(слева доказывается аналогично)
Док-во: Пусть 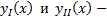 решения ЗК на
решения ЗК на 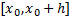 . Тогда
. Тогда 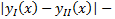 непрерывно, неотрицательно на
непрерывно, неотрицательно на 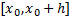 и
и 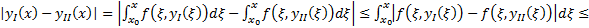 условие Л в П
условие Л в П 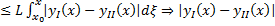 удовлетворяет условию Леммы Гронуолла с
удовлетворяет условию Леммы Гронуолла с 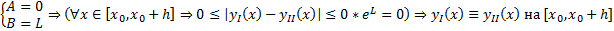 #
#
Вариант 38.
ГЛАВА. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
Основные понятия
Пусть 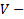 ЛНП (
ЛНП ( 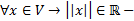 норма
норма
1) 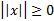 ,причем
,причем 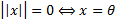
2) 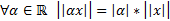
3) 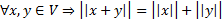 )
)
Напомним, что функционалом называется правило(закон), по которому каждому элементу ЛП ставится в соответствие число.
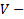 вещественное ЛП
вещественное ЛП
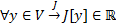
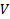 считаем областью задания функционала
считаем областью задания функционала
Замеч. Иногда функционал задан не на всем V, а на некотором его подмножестве 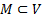 . Тогда М считается областью задания функционала.
. Тогда М считается областью задания функционала.
Основное ЛП, которое мы будем рассматривать, это 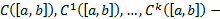 ЛП функций, непрерывных на
ЛП функций, непрерывных на 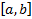 со своими производными до к-го порядка включительно.
со своими производными до к-го порядка включительно.
Норма в 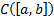 вводится следующим образом :
вводится следующим образом : 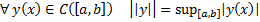
В 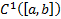
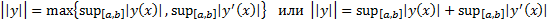
В 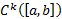
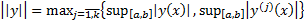 или
или 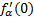 . А в точке
. А в точке 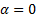
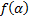 достигает минимума
достигает минимума 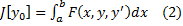
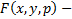 определенная функция 3х переменных (условия на эту функцию уточним позже)
определенная функция 3х переменных (условия на эту функцию уточним позже)
Опр. Задача нахождения экстремума функционала (2) на множестве непрерывных дифференцируемых функций, удовлетворяющих условию (1), называется простейшей задачей вариационного исчисления или задачей с закрытыми концами.
Было показано, что необходимое условие экстремума дифференцируемого функционала является равенство нулю его вариации. Конкретизируем необходимые условия для данного функционала
Замеч. Поскольку концы кривых закреплены, то для всех дополнительных вариаций выполняется, что 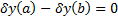
Замеч. 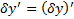
# 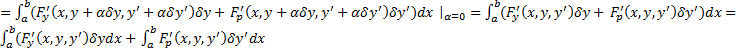 . Рассмотрим второе слагаемое.
. Рассмотрим второе слагаемое. 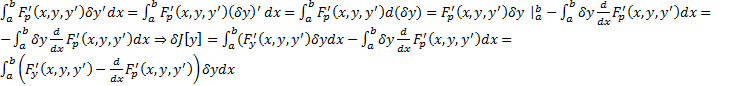 . Если на
. Если на 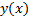 достигается экстремум, то
достигается экстремум, то 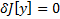 , т.е.
, т.е. 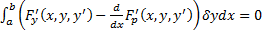 . В силу произвольности
. В силу произвольности 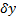 , получаем, что
, получаем, что 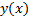 должна удовлетворять уравнению.
должна удовлетворять уравнению.
Опр. 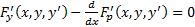 , которое называется уравнением Эйлера.
, которое называется уравнением Эйлера.
Поскольку края 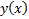 закреплены, то на самом деле
закреплены, то на самом деле 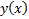 должна являться решением краевой задачи, которая состоит из уравнения Эйлера и критических условий
должна являться решением краевой задачи, которая состоит из уравнения Эйлера и критических условий 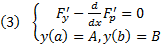
Опр. Она называется краевой задачей Эйлера
Распишем подробно уравнение Эйлера 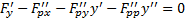 (таким образом, это уравнение 2-го порядка относительно
(таким образом, это уравнение 2-го порядка относительно 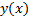 )
)
Мы почти доказали следующее утверждение
Теор. (Необходимое условие экстремума функционала с закрытыми концами)
Пусть 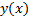 реализует экстремум функционала (2) с закрытыми концами, причем :
реализует экстремум функционала (2) с закрытыми концами, причем :
1) 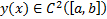
2) 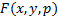 непрерывна со своими производными до 2-го порядка включительно
непрерывна со своими производными до 2-го порядка включительно
Тогда 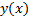 является решением краевой задачи Эйлера (3). Основанием перехода от
является решением краевой задачи Эйлера (3). Основанием перехода от 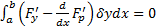 к уравнению Эйлера является Лемма вариационного исчисления
к уравнению Эйлера является Лемма вариационного исчисления
Лемма. (Основная лемма вариационного исчисления)
Пусть 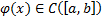 . Если
. Если 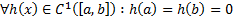 выполнено, что
выполнено, что 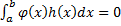 , то
, то 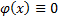 на
на 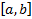
Док-во: (от противного) Допустим, что это не так, т.е. 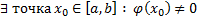 . Поскольку
. Поскольку 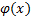 непрерывна, то
непрерывна, то 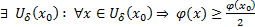 . Рассмотрим
. Рассмотрим 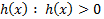 при
при 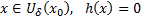 при
при 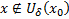 . Тогда
. Тогда 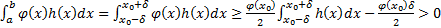 . Получили противоречие(интеграл должен быть равен нулю)
. Получили противоречие(интеграл должен быть равен нулю) 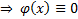 на
на 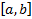 #
#
Замеч. Доказанная теорема дает необходимое условие слабого экстремума, но все, что необходимо для слабого экстремума, необходимо и для сильного .Опр. Всякое решение краевой задачи Эйлера называется экстремалью. То, таким образом, если доказано, что экстремум реализуется на дважды дифференцируемой функции, то это обязательно будет экстремаль.
Замеч. Необходимое условие достаточным не является. Поэтому, вообще говоря, не всякая экстремаль данного функционала реализует его экстремум
Вопрос 40 Обобщение простейшей задачи вариационного исчисления .
Пусть теперь М – множество функций из 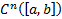 для которого выполняются следующие условия (краевые условия)
для которого выполняются следующие условия (краевые условия)
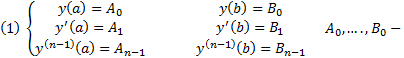 фиксированные числа
фиксированные числа
Рассмотрим на М функционал 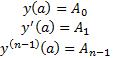
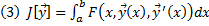
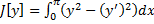
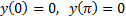
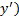
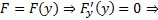 если есть решение этого уравнения, то это константа
если есть решение этого уравнения, то это константа 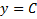 , которая тоже чаще всего не удовлетворяет краевым условиям
, которая тоже чаще всего не удовлетворяет краевым условиям
3) 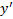 функция. Тогда получим :
функция. Тогда получим : 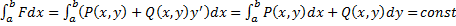 . По любой кривой
. По любой кривой 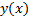 значение интеграла одно и то же, т.е. вариационная задача теряет смысл.
значение интеграла одно и то же, т.е. вариационная задача теряет смысл.
4) 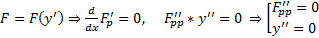 Пусть
Пусть 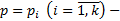 корни уравнения
корни уравнения 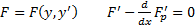 . Домножим обе части на
. Домножим обе части на 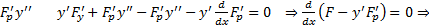 имеется первый интеграл
имеется первый интеграл 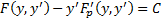 Тоже порядок понизился до первого.
Тоже порядок понизился до первого.
Вопрос 41. Условный экстремум .
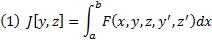
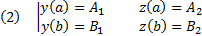
Задача. Найти экстремум функционала (1) с закрытыми концами (2) при наличии дополнительных условий
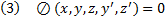
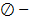 заданная функция своих переменных
заданная функция своих переменных
Эта задача называется задачей нахождения условного экстремума с неголономной связью
Теор. Если пара 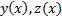 реализует экстремум функционала (1) с закрытыми концами (2) при наличии неголономной связи (3) и выполняются условия :
реализует экстремум функционала (1) с закрытыми концами (2) при наличии неголономной связи (3) и выполняются условия :
1) 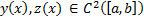
2) 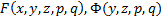 непрерывны со своими частичными производными до 2-го порядка включительно
непрерывны со своими частичными производными до 2-го порядка включительно
3) 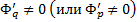
то 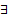 дифференцируемая функция
дифференцируемая функция 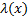 , такая что
, такая что 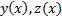 является решением краевой задачи Эйлера для функционала
является решением краевой задачи Эйлера для функционала 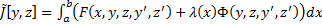 с дополнительными условиями (3), т.е.
с дополнительными условиями (3), т.е.
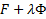
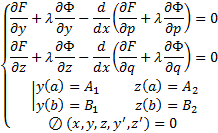
Без док-ва.
Рассмотрим так называемую изопериметрическую задачу. Найти экстремум функционала 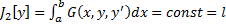 (имеет заданное значение)
(имеет заданное значение)
Часто в качестве 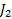 берут функционал
берут функционал 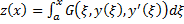 . Тогда
. Тогда 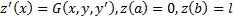 . Таким образом, имеем следующую вариационную задачу : Найти экстремум функционала
. Таким образом, имеем следующую вариационную задачу : Найти экстремум функционала 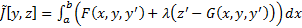 , т.е
, т.е 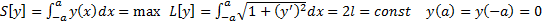 . Рассмотрим
. Рассмотрим 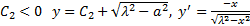
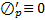 и
и 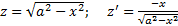
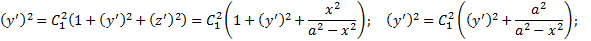
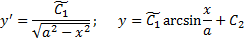
Из граничных условий : 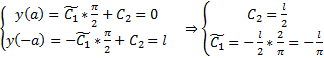
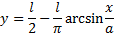
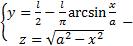 геодезическая линия . Или :
геодезическая линия . Или : 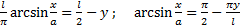
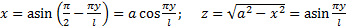 т.е
т.е 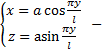 винтовая линия
винтовая линия





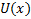 непрерывна и неотрицательна на
непрерывна и неотрицательна на 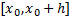 и удовлетворяет условию
и удовлетворяет условию 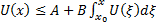 , то
, то 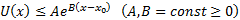
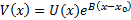 , которая также непрерывна и неотрицательна на
, которая также непрерывна и неотрицательна на 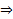 достигает своей верхней грани на
достигает своей верхней грани на 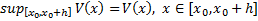
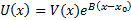
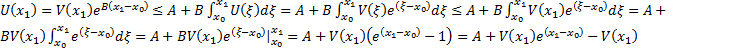
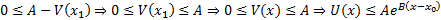 #
#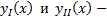 решения ЗК на
решения ЗК на 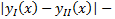 непрерывно, неотрицательно на
непрерывно, неотрицательно на 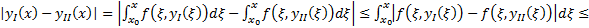 условие Л в П
условие Л в П 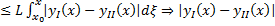 удовлетворяет условию Леммы Гронуолла с
удовлетворяет условию Леммы Гронуолла с 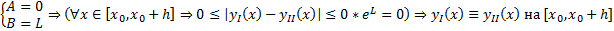 #
#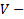 ЛНП (
ЛНП ( 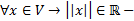 норма
норма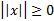 ,причем
,причем 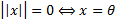
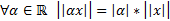
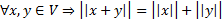 )
) 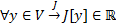
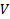 считаем областью задания функционала
считаем областью задания функционала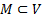 . Тогда М считается областью задания функционала.
. Тогда М считается областью задания функционала.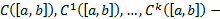 ЛП функций, непрерывных на
ЛП функций, непрерывных на 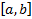 со своими производными до к-го порядка включительно.
со своими производными до к-го порядка включительно.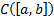 вводится следующим образом :
вводится следующим образом : 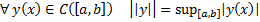
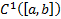
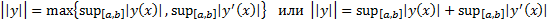
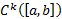
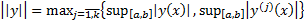 или
или 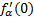 . А в точке
. А в точке 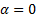
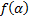 достигает минимума
достигает минимума 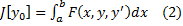
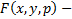 определенная функция 3х переменных (условия на эту функцию уточним позже)
определенная функция 3х переменных (условия на эту функцию уточним позже)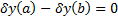
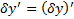
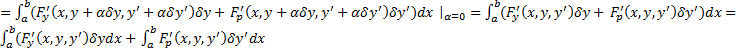 . Рассмотрим второе слагаемое.
. Рассмотрим второе слагаемое. 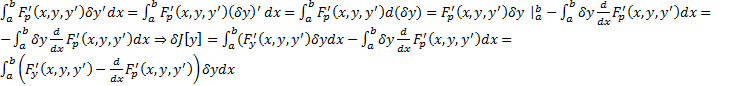 . Если на
. Если на 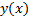 достигается экстремум, то
достигается экстремум, то 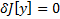 , т.е.
, т.е. 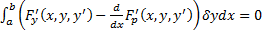 . В силу произвольности
. В силу произвольности 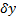 , получаем, что
, получаем, что 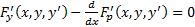 , которое называется уравнением Эйлера.
, которое называется уравнением Эйлера.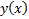 закреплены, то на самом деле
закреплены, то на самом деле 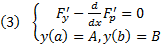
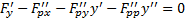 (таким образом, это уравнение 2-го порядка относительно
(таким образом, это уравнение 2-го порядка относительно 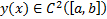
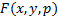 непрерывна со своими производными до 2-го порядка включительно
непрерывна со своими производными до 2-го порядка включительно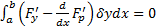 к уравнению Эйлера является Лемма вариационного исчисления
к уравнению Эйлера является Лемма вариационного исчисления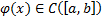 . Если
. Если 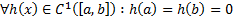 выполнено, что
выполнено, что 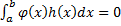 , то
, то 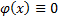 на
на 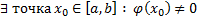 . Поскольку
. Поскольку 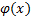 непрерывна, то
непрерывна, то 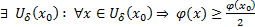 . Рассмотрим
. Рассмотрим 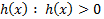 при
при 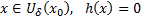 при
при 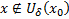 . Тогда
. Тогда 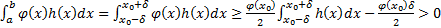 . Получили противоречие(интеграл должен быть равен нулю)
. Получили противоречие(интеграл должен быть равен нулю) 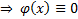 на
на 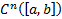 для которого выполняются следующие условия (краевые условия)
для которого выполняются следующие условия (краевые условия)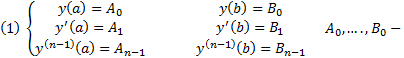 фиксированные числа
фиксированные числа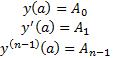
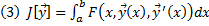
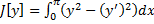
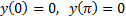
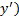
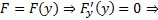 если есть решение этого уравнения, то это константа
если есть решение этого уравнения, то это константа 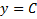 , которая тоже чаще всего не удовлетворяет краевым условиям
, которая тоже чаще всего не удовлетворяет краевым условиям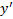 функция. Тогда получим :
функция. Тогда получим : 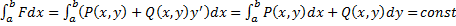 . По любой кривой
. По любой кривой 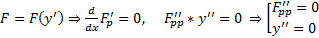 Пусть
Пусть 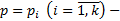 корни уравнения
корни уравнения 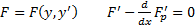 . Домножим обе части на
. Домножим обе части на 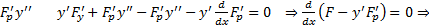 имеется первый интеграл
имеется первый интеграл 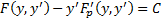 Тоже порядок понизился до первого.
Тоже порядок понизился до первого.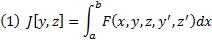
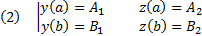
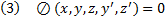
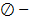 заданная функция своих переменных
заданная функция своих переменных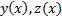 реализует экстремум функционала (1) с закрытыми концами (2) при наличии неголономной связи (3) и выполняются условия :
реализует экстремум функционала (1) с закрытыми концами (2) при наличии неголономной связи (3) и выполняются условия :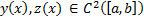
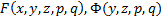 непрерывны со своими частичными производными до 2-го порядка включительно
непрерывны со своими частичными производными до 2-го порядка включительно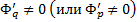
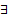 дифференцируемая функция
дифференцируемая функция 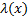 , такая что
, такая что 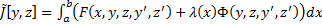 с дополнительными условиями (3), т.е.
с дополнительными условиями (3), т.е.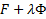
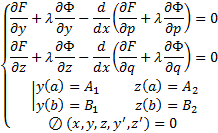
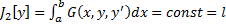 (имеет заданное значение)
(имеет заданное значение)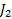 берут функционал
берут функционал 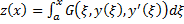 . Тогда
. Тогда 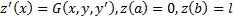 . Таким образом, имеем следующую вариационную задачу : Найти экстремум функционала
. Таким образом, имеем следующую вариационную задачу : Найти экстремум функционала 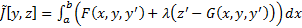 , т.е
, т.е 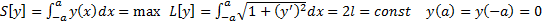 . Рассмотрим
. Рассмотрим 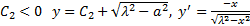
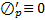 и
и 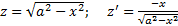
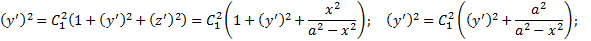
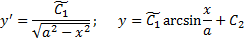
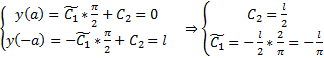
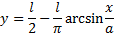
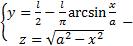 геодезическая линия . Или :
геодезическая линия . Или : 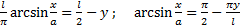
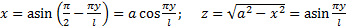 т.е
т.е 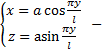 винтовая линия
винтовая линия


