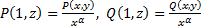В простейшем случае методика решения ОДУ следующая : предположим, что решение 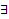 , подставим его в уравнение и получим тождество. Из тождества равносильными преобразованиями получим общее решение. Проверить подстановкой в уравнение.
, подставим его в уравнение и получим тождество. Из тождества равносильными преобразованиями получим общее решение. Проверить подстановкой в уравнение.
Уравнения с разделяющимися переменными
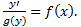
Подставляя сюда предполагаемое решение, получаем тождество, которое проинтегрируем по 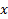
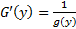 сохраняет знак
сохраняет знак 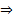
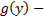 строго монотонная функция
строго монотонная функция 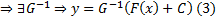 . Проверим, что (3) определяет общее решение. Пусть
. Проверим, что (3) определяет общее решение. Пусть 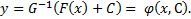
Тогда 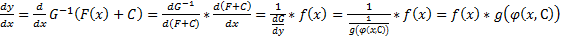 , т.е. обращают (1) в тождество
, т.е. обращают (1) в тождество 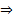 (3) общее решение, а (2) – общий интеграл.
(3) общее решение, а (2) – общий интеграл.
Замеч. Если в какой-либо точке 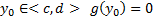 , то функция
, то функция 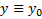 тоже является решением уравнения (1) и его нужно присоединить к (3)
тоже является решением уравнения (1) и его нужно присоединить к (3)
Опр. Выражения 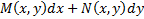 ( M,N- известные функции двух переменных, dx,dy – дифференциалы переменных x, y) называется дифференциальной формой, а уравнения
( M,N- известные функции двух переменных, dx,dy – дифференциалы переменных x, y) называется дифференциальной формой, а уравнения 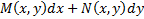 =0 – уравнением в дифференциалах. Его решением называется каждое из решений ОДУ 1-го порядка
=0 – уравнением в дифференциалах. Его решением называется каждое из решений ОДУ 1-го порядка 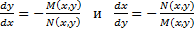 .
.
Наиболее общий вид уравнения с разделяющимися переменными 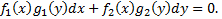 Решается аналогичным образом.
Решается аналогичным образом.
Рассмотрим уравнение 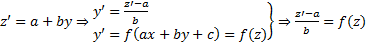
(10) 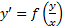
(12) 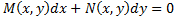 , где M,N – однородные функции одной степени однородности
, где M,N – однородные функции одной степени однородности
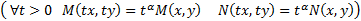
Опр. Уравнения (11) и (12) называется однородными ОДУ
Заменой 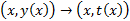 , где
, где 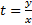 однородные ОДУ сводятся к уравнениям с разделяющимися переменными
однородные ОДУ сводятся к уравнениям с разделяющимися переменными
Док-во: 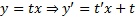 ;
; 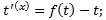
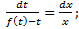
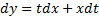 (12)
(12)
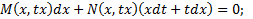
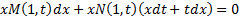
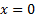
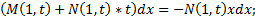
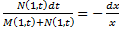
К однородным сводятся уравнения вида 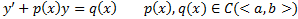
Опр.(21) называется линейным ОДУ 1-го порядка. Если 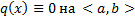 , то оно называется линейным однородным. В противоположном случае – линейным неоднородным.
, то оно называется линейным однородным. В противоположном случае – линейным неоднородным.
Метод вариации произвольных постоянных
1. Рассмотрим соответствующее однородное уравнение. Оно всегда является уравнением с разделяющимися переменными : 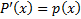 . Тогда
. Тогда 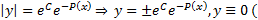 так как является решением этого уравнения)
так как является решением этого уравнения) 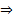 общее решение однородного уравнения можно записать в виде
общее решение однородного уравнения можно записать в виде 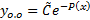
(где 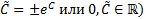
2. Для решения неоднородного уравнения сделаем замену переменных. 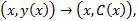 где
где 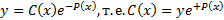 Тогда
Тогда 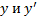 в (21) получим
в (21) получим 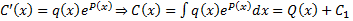
Тогда 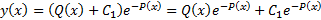
Теор.(Об общем решении неоднородного линейного ОДУ 1-го порядка) 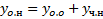
Уравнение Бернулли
(31) 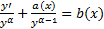 . Полагаем
. Полагаем 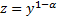 . Тогда
. Тогда 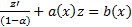
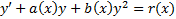 , где
, где 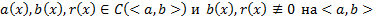
(41) называется уравнением Риккати
1841 г. Лиувиль доказал, что оно не интегрируемо в квадратурах в общем случае. Но если каким-либо образом известно частное решение этого уравнения, то общее решение можно найти путем сведения его к уравнению Бернулли заменой 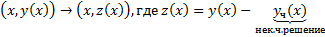 .
.
Разность любых двух частных решений уравнения Риккати является решением уравнения Бернулли.
Док-во: Пусть 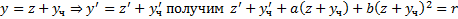
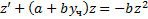
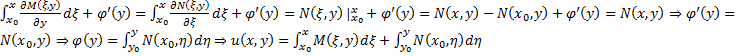 . Соответственно общим интегралом УПД будет соотношение
. Соответственно общим интегралом УПД будет соотношение 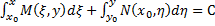 а решением ЗК (62) неявно задается соотношением
а решением ЗК (62) неявно задается соотношением 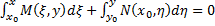
Интегрирующий множитель
Пусть 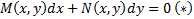 не является УПД
не является УПД
Опр. Если существует дифференцируемая функция для 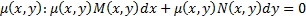 становится УПД,
становится УПД, 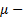 называется интегрирующий множителем уравнения (*)
называется интегрирующий множителем уравнения (*)
Каким условием должна удовлетворять 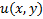
В одной области
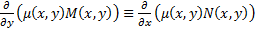 или
или 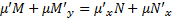 , т.е.
, т.е. 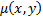 должна удовлетворять уравнению в частных производных
должна удовлетворять уравнению в частных производных 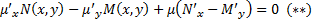 . В общем случае это уравнение решить еще труднее чем исходное (*). Известно, что при непрерывном дифференцировании
. В общем случае это уравнение решить еще труднее чем исходное (*). Известно, что при непрерывном дифференцировании 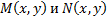 не обращ в ноль одновременно, инт. множитель уравнения (*) существует.
не обращ в ноль одновременно, инт. множитель уравнения (*) существует.
Их существует 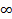 много(инт. множество), а для того, чтобы решить уравнение, достаточно одной такой функции. Покажем, при каких условиях уравнение (*) имеет интегрирующий множитель специального вида, например
много(инт. множество), а для того, чтобы решить уравнение, достаточно одной такой функции. Покажем, при каких условиях уравнение (*) имеет интегрирующий множитель специального вида, например
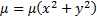 . Обозначение:
. Обозначение: 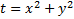 . Тогда
. Тогда 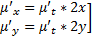 подставим в (**), получим :
подставим в (**), получим : 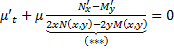
(***) 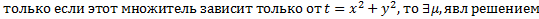 ОДУ
ОДУ
Рассмотрим некоторые частные случаи, когда интегрирующий множитель легко находится.
Пусть 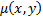 не зависит от y, т.е.
не зависит от y, т.е. 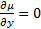 . Тогда инт. мн-ль находится из ур-я:
. Тогда инт. мн-ль находится из ур-я: 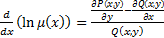
Пусть 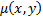 не зависит от x, т.е.
не зависит от x, т.е. 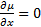 . Тогда инт. мн-ль находится из ур-я:
. Тогда инт. мн-ль находится из ур-я: 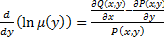
Пусть P(x,y) и Q(x,y) – однор. ф-ии порядка  . Введем
. Введем 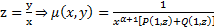 , где
, где 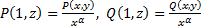





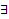 , подставим его в уравнение и получим тождество. Из тождества равносильными преобразованиями получим общее решение. Проверить подстановкой в уравнение.
, подставим его в уравнение и получим тождество. Из тождества равносильными преобразованиями получим общее решение. Проверить подстановкой в уравнение.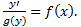
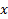
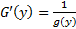 сохраняет знак
сохраняет знак 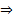
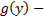 строго монотонная функция
строго монотонная функция 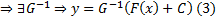 . Проверим, что (3) определяет общее решение. Пусть
. Проверим, что (3) определяет общее решение. Пусть 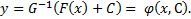
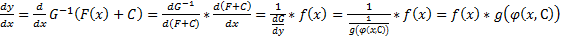 , т.е. обращают (1) в тождество
, т.е. обращают (1) в тождество 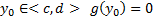 , то функция
, то функция 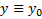 тоже является решением уравнения (1) и его нужно присоединить к (3)
тоже является решением уравнения (1) и его нужно присоединить к (3)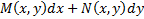 ( M,N- известные функции двух переменных, dx,dy – дифференциалы переменных x, y) называется дифференциальной формой, а уравнения
( M,N- известные функции двух переменных, dx,dy – дифференциалы переменных x, y) называется дифференциальной формой, а уравнения 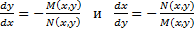 .
. 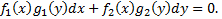 Решается аналогичным образом.
Решается аналогичным образом.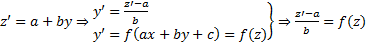
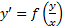
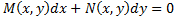 , где M,N – однородные функции одной степени однородности
, где M,N – однородные функции одной степени однородности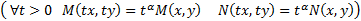
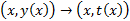 , где
, где 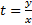 однородные ОДУ сводятся к уравнениям с разделяющимися переменными
однородные ОДУ сводятся к уравнениям с разделяющимися переменными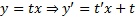 ;
; 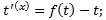
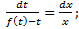
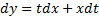 (12)
(12)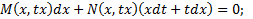
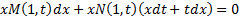
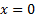
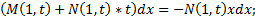
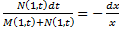
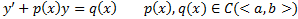
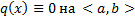 , то оно называется линейным однородным. В противоположном случае – линейным неоднородным.
, то оно называется линейным однородным. В противоположном случае – линейным неоднородным.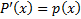 . Тогда
. Тогда 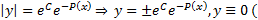 так как является решением этого уравнения)
так как является решением этого уравнения) 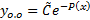
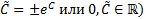
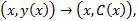 где
где 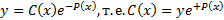 Тогда
Тогда 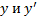 в (21) получим
в (21) получим 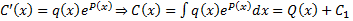
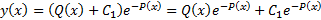
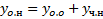
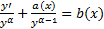 . Полагаем
. Полагаем 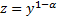 . Тогда
. Тогда 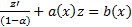
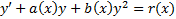 , где
, где 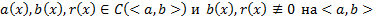
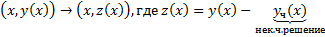 .
.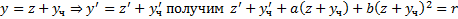
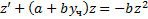
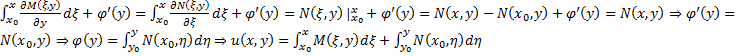 . Соответственно общим интегралом УПД будет соотношение
. Соответственно общим интегралом УПД будет соотношение 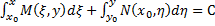 а решением ЗК (62) неявно задается соотношением
а решением ЗК (62) неявно задается соотношением 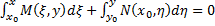
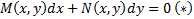 не является УПД
не является УПД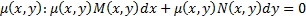 становится УПД,
становится УПД, 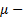 называется интегрирующий множителем уравнения (*)
называется интегрирующий множителем уравнения (*)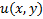
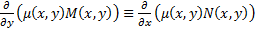 или
или 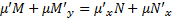 , т.е.
, т.е. 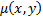 должна удовлетворять уравнению в частных производных
должна удовлетворять уравнению в частных производных 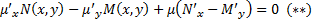 . В общем случае это уравнение решить еще труднее чем исходное (*). Известно, что при непрерывном дифференцировании
. В общем случае это уравнение решить еще труднее чем исходное (*). Известно, что при непрерывном дифференцировании 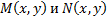 не обращ в ноль одновременно, инт. множитель уравнения (*) существует.
не обращ в ноль одновременно, инт. множитель уравнения (*) существует.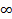 много(инт. множество), а для того, чтобы решить уравнение, достаточно одной такой функции. Покажем, при каких условиях уравнение (*) имеет интегрирующий множитель специального вида, например
много(инт. множество), а для того, чтобы решить уравнение, достаточно одной такой функции. Покажем, при каких условиях уравнение (*) имеет интегрирующий множитель специального вида, например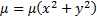 . Обозначение:
. Обозначение: 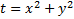 . Тогда
. Тогда 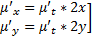 подставим в (**), получим :
подставим в (**), получим : 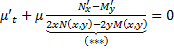
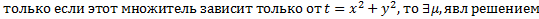 ОДУ
ОДУ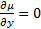 . Тогда инт. мн-ль находится из ур-я:
. Тогда инт. мн-ль находится из ур-я: 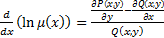
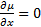 . Тогда инт. мн-ль находится из ур-я:
. Тогда инт. мн-ль находится из ур-я: 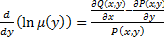
 . Введем
. Введем 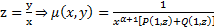 , где
, где