Опр. Огибающей S семейство кривых называется линия, которая в каждой своей точке касается некоторой кривой(прямой) этого семейства, не совпадая с S в сколь угодно малой окрестности этой точки.
Рассмотрим уравнение Клеро
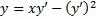
Решим его: 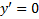
По крайней мере 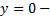 решение и
решение и 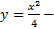 решение, т.е. в случае 3) происходит нарушение единственности решения ЗК
решение, т.е. в случае 3) происходит нарушение единственности решения ЗК
Опр. Множество точек, в которых нарушается единственность решения ЗК называется особым множеством. Если это особое множество представляет собой интегр. кривую исходного ДУ, не разрешенного относительно производных, то говорят об особом решении. В частности, огибающая уравнение Клеро является особым решением этого уравнения.
Особые решения уравнения, не разрешенных относительно производных.
Рассмотрим (1) 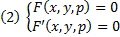
Всякая кривая, являющаяся решением этой системы называется Р-дискриминантной кривой.
В частности, особое решение (если существует) является Р-дискриминантной кривой. Однако з-дискриминантная кривая не обязана является особым решением.
Вообще р-дискриминантная кривая может быть:
 Огибание
Огибание
Точки заострения 
Точки прикосновения
Ассимптотич. 
Из всех этих случаев только огибающая является особым решением
Таким образом особое решение всегда непрерывно дифференцируема 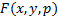 ищем по схеме:
ищем по схеме:
1) Отыскиваем всевозможные з-дискриминантные кривые (они являются решением системы (2))
2) Проверяем, являютcя ли эти кривые интегральными кривыми уравнения 
Поскольку 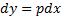
С другой стороны 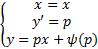
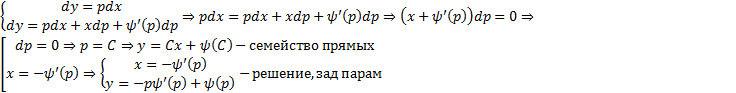
Таким образом, всевозможные решения уравнения Клеро 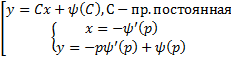
Как соотносятся эти решения? Можно показать, что кривая 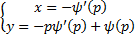 являются огибающей семейство прямых
являются огибающей семейство прямых 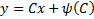 , если
, если 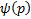 не является линейной функцией.
не является линейной функцией.





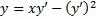
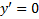
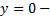 решение и
решение и 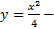 решение, т.е. в случае 3) происходит нарушение единственности решения ЗК
решение, т.е. в случае 3) происходит нарушение единственности решения ЗК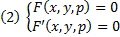
 Огибание
Огибание


 ищем по схеме:
ищем по схеме:
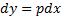
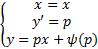
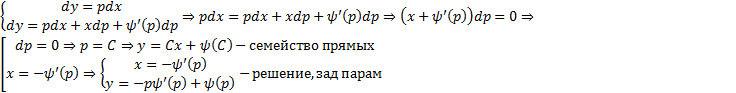
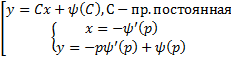
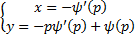 являются огибающей семейство прямых
являются огибающей семейство прямых 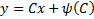 , если
, если 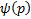 не является линейной функцией.
не является линейной функцией.


