Вопрос 1 . ОДУ 1-го порядка. Основные определения.

Пусть 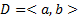 один из промежутков  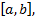( 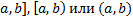, где 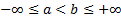. Будем говорить, что 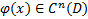, если 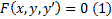, где 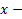независимая переменная, а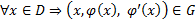

2) 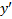, то оно принимает вид : 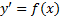. Его общим решением будет 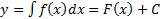. В дальнейшем увидим, что это является общей ситуацией, т.е. общее решение ОДУ 1-го порядка содержит 1 произвольную постоянную. На плоскости общее решение будет представлять собой совокупность интегральных кривых.

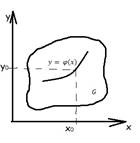
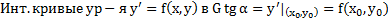
Опр. В области существования и единственности решение ЗК общим решением уравнения (2) называется дифференцируемая функция 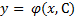 такая, что :

1) Для 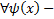частное решение ОДУ (2)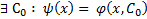

2) Для 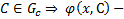решение (2)

Опр. Соотношени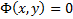е , где 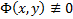 на D, называют частным интегралом на D уравнения (2), если  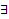решение уравнения (2)  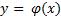такое, что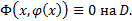

Замеч. Из частного интеграла по теореме о неявной функции может быть получено частное решение ОДУ (2)

Опр. Общим интегралом уравнения наз. ф-ия 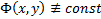, но сохраняющая постоянное значение на любом решении уравнения (2). Иногда общим интегралом называется само соотношение  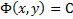или более общее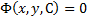

Замеч. Из общего интеграла по теореме о неявной функции может быть получено общее решение.

Вопрос 2.

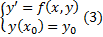. Второе условие в системе называется начальным условием ЗК.

В каждой точке 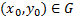 уравнение(2) однозначно определяет направление касательной  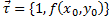к интегральной кривой, проходящей через эту точку.

Интегральные кривые уравнения (2) не могут пересекаться (могут только касаться).

В случае касания ЗК в окрестности этой точки имеет не единственное решение.

Теор. (О существовании и единственности решения ЗК для уравнения (2)) (далее ТСЕ)

Пусть 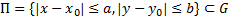. Есл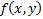и  и 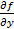 непрерывны в П по совокупности переменных, то  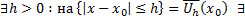решение ЗК (3), причем единственно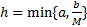е. ( , где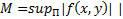

Замеч. 

1) Теорема имеет локальный характер, т.е. гарантирует, что решение существует в некоторой окрестности точки 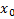. Однако во всей  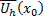гарантируется единственность решения понимаемое в следующем смысле. Пусть 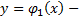решение ЗК(3) на  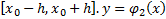– какое-либо решение ЗК(3) н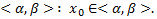а Тогд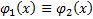а  на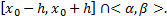

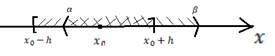
2) Решение ЗК(3) существует при выполнении только лишь условия 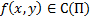, но при этом не гарантируется единственность.

3) Условие 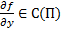 можно заменить на  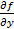огр в П или условие Липшица.

4) Эта теорема является достаточным условием

5) Если при движении по отрезку 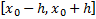 в других точках также выполняестя условие ТСЕ, то решение часто удается продлить дальше, иногда на полупрямую и всю прямую.