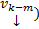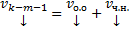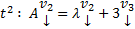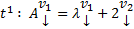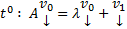(1) 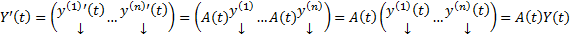 , то матрица решений формально тоже удовлетворяет ОСЛОДУ (1), т.е.
, то матрица решений формально тоже удовлетворяет ОСЛОДУ (1), т.е. 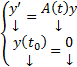 Но эта ЗК обладает тривиальным решением
Но эта ЗК обладает тривиальным решением 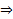 по ТСЕ
по ТСЕ 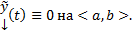 Т.о.
Т.о. 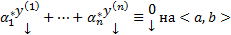 то
то 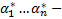 нетривиальный набор
нетривиальный набор 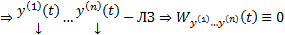 на
на 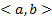
Замеч. Если 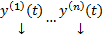 не является решениями ОСЛОДУ (1) с непрерывными коэффициентами то это свойство не обязано выполнятся
не является решениями ОСЛОДУ (1) с непрерывными коэффициентами то это свойство не обязано выполнятся
3) Пусть 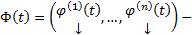 ФМР для ОСЛОДУ (1) , то
ФМР для ОСЛОДУ (1) , то 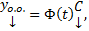 где
где 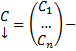 столбец произвольных постоянных
столбец произвольных постоянных
Док-во: 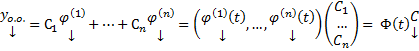
4) Если Ф(t) – ФМР ОСЛОДУ (1), то с непрерывными коэффициентами ЗК 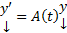 , то
, то 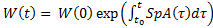 , где
, где 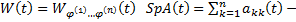 след матрицы A(t)
след матрицы A(t)
Док-во: Докажем для n=2. Пусть 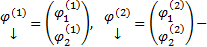 ФСР ОСЛОДУ
ФСР ОСЛОДУ 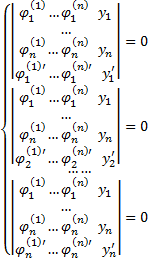
Каждый из столбцов 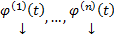 удовлетворяет этой ОСЛОДУ. Раскроем теперь все определители по последнему столбцу, получим :
удовлетворяет этой ОСЛОДУ. Раскроем теперь все определители по последнему столбцу, получим : 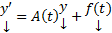
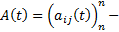 непрерывные на
непрерывные на 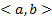 коэффициенты
коэффициенты 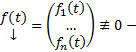 правые части
правые части
Рассмотрим соответствующую ОСЛОДУ 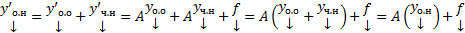 . Покажем теперь, что любое решение СЛОДУ (1) входит в (3). Пусть
. Покажем теперь, что любое решение СЛОДУ (1) входит в (3). Пусть 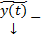 произвольное решение (1). Рассмотрим разность
произвольное решение (1). Рассмотрим разность 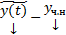 . Покажем, что эта разность удовлетворяет (2).
. Покажем, что эта разность удовлетворяет (2). 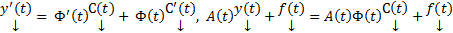 ,
, 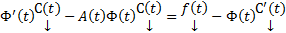 ,
, 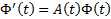 . Тогда
. Тогда 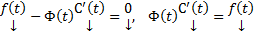
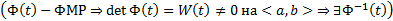
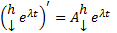
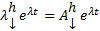 Поскольку
Поскольку 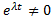 , то
, то 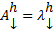 . Если нас интересует нетривиальные решения, то
. Если нас интересует нетривиальные решения, то 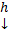 должно быть нетривиальное решение ОСЛАУ (2)
должно быть нетривиальное решение ОСЛАУ (2) 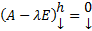 квадр ОСЛАУ (2) имеет нетривиальные решения
квадр ОСЛАУ (2) имеет нетривиальные решения 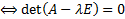
Опр. Уравнение 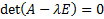 называется характеристическим уравнением.
называется характеристическим уравнением.
Известно, что в поле 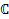 оно имеет n корней с учетом их кратности.
оно имеет n корней с учетом их кратности.
Замеч. Фактически 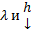 являются соответственно СЗ и комп СВ ЛО, имеющего в некотором базисе матрицу А.
являются соответственно СЗ и комп СВ ЛО, имеющего в некотором базисе матрицу А.
Получаем, что 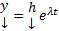 является нетривиальным решением ОСЛООДУ (1)
является нетривиальным решением ОСЛООДУ (1) 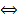
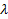 является корнем характеристического уравнения, а
является корнем характеристического уравнения, а 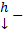 соответственно СВ.
соответственно СВ.
Построение ФСР ОСЛОДУ (1)
Все корни характеристического уравнения вещественны и различны. Т.е. имеем набор решений 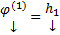
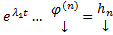
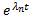
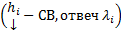 . Поскольку
. Поскольку 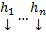
 отвечают различным С, то они ЛНЗ. Покажем, что
отвечают различным С, то они ЛНЗ. Покажем, что 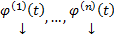 образуют ФСР ОСЛОДУ (1), т.е. является ЛНЗ на
образуют ФСР ОСЛОДУ (1), т.е. является ЛНЗ на 
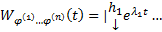
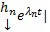
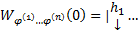
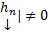 т.к. в столбцах det записаны координаты ЛНЗ векторов
т.к. в столбцах det записаны координаты ЛНЗ векторов 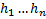 .
. 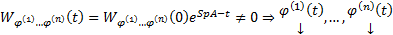 ЛНЗ на всей
ЛНЗ на всей 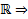 это ФСР ОСЛОДУ (1)
это ФСР ОСЛОДУ (1)
Замеч. В рассматриваемом случае предполагалось, что А – вещественная матрица и была построена соответствующими вещ ФСР
Если А – комплексная матрица и все корни характеристического уравнения различны, то ФСР 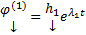
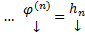
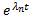 будет комплекснозначной. Тогда всевозможные ЛК элементов этой ФСР с комплексными коэффициентами дадут всевозможные комплексные решения ОСЛОДУ (1)
будет комплекснозначной. Тогда всевозможные ЛК элементов этой ФСР с комплексными коэффициентами дадут всевозможные комплексные решения ОСЛОДУ (1)
Вопрос 21.
(1) 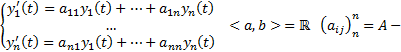 постоянная матрица, т.е.
постоянная матрица, т.е. 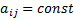
Будем искать решение это системы в виде 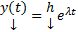
Подставим в (1) получим : 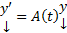
Будем искать ее решение в виде 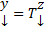 . Где Т – построенная невырожденная матрица. Тогда
. Где Т – построенная невырожденная матрица. Тогда 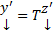
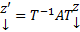 Допустим, что матрица А диагонализуема (т.е. линейный оператор, которому она отвечает в некотором базисе имеет диагонализуемую матрицу. Это возможно
Допустим, что матрица А диагонализуема (т.е. линейный оператор, которому она отвечает в некотором базисе имеет диагонализуемую матрицу. Это возможно 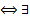 базис из СВ этого ЛО
базис из СВ этого ЛО 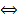 у всех его СЗ АК=ГК. В этом случае Т представляет собой матрицу, в столбцах которой записаны координаты собственных векторов ) Предположим, что
у всех его СЗ АК=ГК. В этом случае Т представляет собой матрицу, в столбцах которой записаны координаты собственных векторов ) Предположим, что 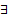 базис из СВ. Тогда
базис из СВ. Тогда 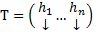
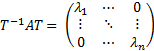 Тогда получим, что
Тогда получим, что 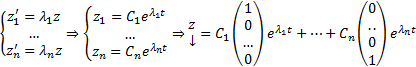
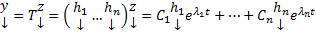 Таким образом независимо от того являются ли корни характеристического уравнения простыми или нет, в случае, когда
Таким образом независимо от того являются ли корни характеристического уравнения простыми или нет, в случае, когда 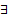 базис из СВ, отвечающий этим СЗ, ФСР имеет один и тот же вид, а именно
базис из СВ, отвечающий этим СЗ, ФСР имеет один и тот же вид, а именно 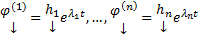 с той лишь разницей, что в случае кратных корней некоторые
с той лишь разницей, что в случае кратных корней некоторые 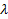 могут совпадать.
могут совпадать.
В случае когда хотя бы для одного 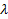 АК > ГК (ради определенности пусть АК =k, ГК=m m<k) можно показать, что
АК > ГК (ради определенности пусть АК =k, ГК=m m<k) можно показать, что 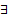 k ЛНЗ решений, отвечающих такому
k ЛНЗ решений, отвечающих такому 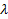 , который имеет вид
, который имеет вид 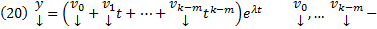 столбцы подлежащие определению : Как их отыскать ? Подставим (20) в
столбцы подлежащие определению : Как их отыскать ? Подставим (20) в 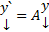 получим тождество
получим тождество 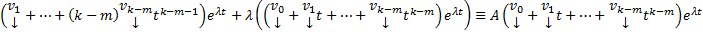 Далее приравниваем коэффициенты при одинаковых степенях t получим :
Далее приравниваем коэффициенты при одинаковых степенях t получим :
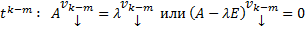
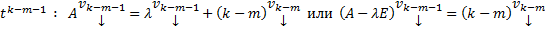
…………..
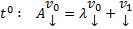
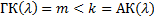
Теор. 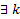 ЛНЗ решений вида
ЛНЗ решений вида 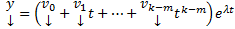 , отвечающих этому СЗ(без док-ва)
, отвечающих этому СЗ(без док-ва)
Подставим в ОСЛОДУ, получим, что 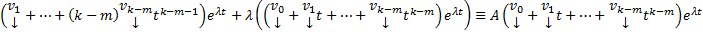
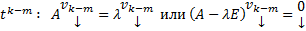 , т.о.
, т.о. 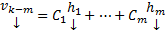
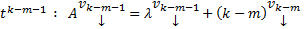 Эта система обладает расширенной матрицей
Эта система обладает расширенной матрицей 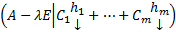 и совместна при всех значениях
и совместна при всех значениях 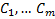 . Из условия совместимости получаем ограничения на
. Из условия совместимости получаем ограничения на 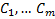 , т.е. связь между ними, т.е. будет зависеть
, т.е. связь между ними, т.е. будет зависеть 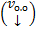 от m новых констант
от m новых констант 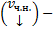 будет зависеть от некоторых старых (это же касается
будет зависеть от некоторых старых (это же касается 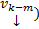
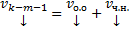
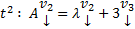
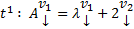
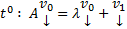
Постепенно, спускаясь вниз, будем на каждом шаге получать m новых констант и дополнительных ограничений на старые константы. В конце останется k констант. Собирая коэффициенты при них мы получим k элементов ФСР отвечающих данному 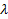 .
.





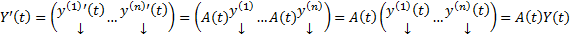 , то матрица решений формально тоже удовлетворяет ОСЛОДУ (1), т.е.
, то матрица решений формально тоже удовлетворяет ОСЛОДУ (1), т.е. 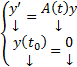 Но эта ЗК обладает тривиальным решением
Но эта ЗК обладает тривиальным решением 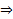 по ТСЕ
по ТСЕ 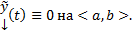 Т.о.
Т.о. 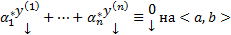 то
то 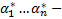 нетривиальный набор
нетривиальный набор 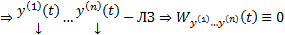 на
на 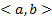
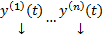 не является решениями ОСЛОДУ (1) с непрерывными коэффициентами то это свойство не обязано выполнятся
не является решениями ОСЛОДУ (1) с непрерывными коэффициентами то это свойство не обязано выполнятся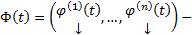 ФМР для ОСЛОДУ (1) , то
ФМР для ОСЛОДУ (1) , то 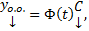 где
где 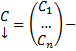 столбец произвольных постоянных
столбец произвольных постоянных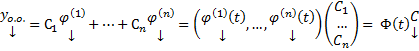
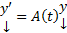 , то
, то 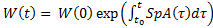 , где
, где 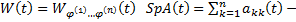 след матрицы A(t)
след матрицы A(t) 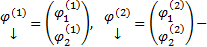 ФСР ОСЛОДУ
ФСР ОСЛОДУ 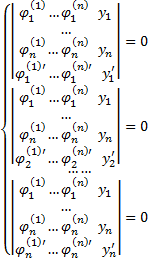
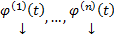 удовлетворяет этой ОСЛОДУ. Раскроем теперь все определители по последнему столбцу, получим :
удовлетворяет этой ОСЛОДУ. Раскроем теперь все определители по последнему столбцу, получим : 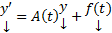
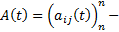 непрерывные на
непрерывные на 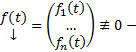 правые части
правые части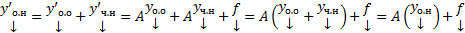 . Покажем теперь, что любое решение СЛОДУ (1) входит в (3). Пусть
. Покажем теперь, что любое решение СЛОДУ (1) входит в (3). Пусть 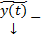 произвольное решение (1). Рассмотрим разность
произвольное решение (1). Рассмотрим разность 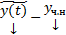 . Покажем, что эта разность удовлетворяет (2).
. Покажем, что эта разность удовлетворяет (2). 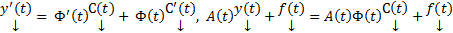 ,
, 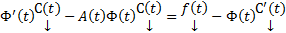 ,
, 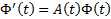 . Тогда
. Тогда 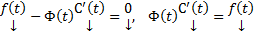
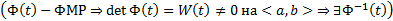
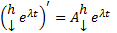
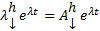 Поскольку
Поскольку 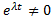 , то
, то 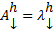 . Если нас интересует нетривиальные решения, то
. Если нас интересует нетривиальные решения, то 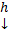 должно быть нетривиальное решение ОСЛАУ (2)
должно быть нетривиальное решение ОСЛАУ (2) 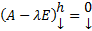 квадр ОСЛАУ (2) имеет нетривиальные решения
квадр ОСЛАУ (2) имеет нетривиальные решения 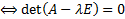
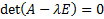 называется характеристическим уравнением.
называется характеристическим уравнением.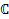 оно имеет n корней с учетом их кратности.
оно имеет n корней с учетом их кратности.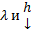 являются соответственно СЗ и комп СВ ЛО, имеющего в некотором базисе матрицу А.
являются соответственно СЗ и комп СВ ЛО, имеющего в некотором базисе матрицу А.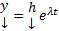 является нетривиальным решением ОСЛООДУ (1)
является нетривиальным решением ОСЛООДУ (1) 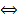
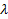 является корнем характеристического уравнения, а
является корнем характеристического уравнения, а 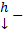 соответственно СВ.
соответственно СВ.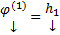
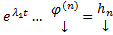
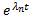
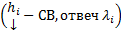 . Поскольку
. Поскольку 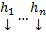
 отвечают различным С, то они ЛНЗ. Покажем, что
отвечают различным С, то они ЛНЗ. Покажем, что 
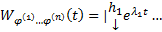
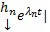
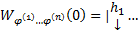
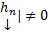 т.к. в столбцах det записаны координаты ЛНЗ векторов
т.к. в столбцах det записаны координаты ЛНЗ векторов 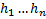 .
. 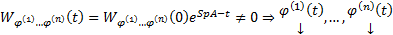 ЛНЗ на всей
ЛНЗ на всей 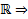 это ФСР ОСЛОДУ (1)
это ФСР ОСЛОДУ (1) 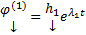
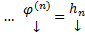
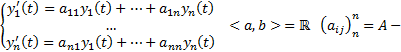 постоянная матрица, т.е.
постоянная матрица, т.е. 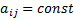
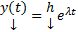
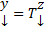 . Где Т – построенная невырожденная матрица. Тогда
. Где Т – построенная невырожденная матрица. Тогда 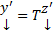
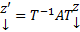 Допустим, что матрица А диагонализуема (т.е. линейный оператор, которому она отвечает в некотором базисе имеет диагонализуемую матрицу. Это возможно
Допустим, что матрица А диагонализуема (т.е. линейный оператор, которому она отвечает в некотором базисе имеет диагонализуемую матрицу. Это возможно 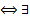 базис из СВ этого ЛО
базис из СВ этого ЛО 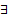 базис из СВ. Тогда
базис из СВ. Тогда 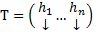
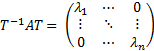 Тогда получим, что
Тогда получим, что 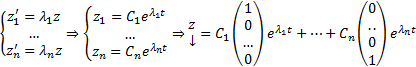
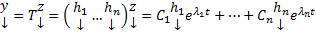 Таким образом независимо от того являются ли корни характеристического уравнения простыми или нет, в случае, когда
Таким образом независимо от того являются ли корни характеристического уравнения простыми или нет, в случае, когда 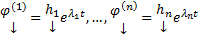 с той лишь разницей, что в случае кратных корней некоторые
с той лишь разницей, что в случае кратных корней некоторые 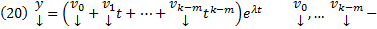 столбцы подлежащие определению : Как их отыскать ? Подставим (20) в
столбцы подлежащие определению : Как их отыскать ? Подставим (20) в 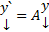 получим тождество
получим тождество 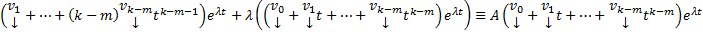 Далее приравниваем коэффициенты при одинаковых степенях t получим :
Далее приравниваем коэффициенты при одинаковых степенях t получим :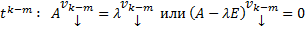
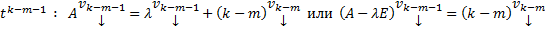
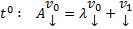
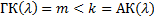
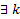 ЛНЗ решений вида
ЛНЗ решений вида 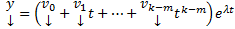 , отвечающих этому СЗ(без док-ва)
, отвечающих этому СЗ(без док-ва)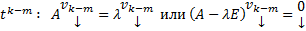 , т.о.
, т.о. 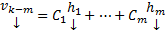
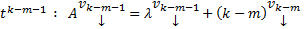 Эта система обладает расширенной матрицей
Эта система обладает расширенной матрицей 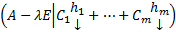 и совместна при всех значениях
и совместна при всех значениях 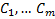 . Из условия совместимости получаем ограничения на
. Из условия совместимости получаем ограничения на 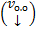 от m новых констант
от m новых констант 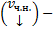 будет зависеть от некоторых старых (это же касается
будет зависеть от некоторых старых (это же касается