Представления о направленности связи и теория гибридизации электронных орбиталей позволяют объяснить геометрическую форму молекул веществ с ковалентными связями, но не могут предсказать ее. Теоретический расчет геометрической конфигурации частицы квантово-механическими методами представляет собой очень сложную и не всегда имеющую однозначное решение задачу. Однако существует довольно простой прием, позволяющий с достаточно высокой надежностью качественно оценить геометрию молекул. Этот прием был разработан Р. Гиллеспи и получил название: метод отталкивания электронных пар валентной оболочки. Метод связывает форму частицы с силами отталкивания, действующими между электронными парами, сформированными при образовании соответствующей молекулы. Метод Гиллеспи особо результативен для молекул, образованных s- и р-элементами.
Концепция отталкивания электронных пар валентной оболочки может быть сведена к следующим основным положениям:
1. Геометрическая форма молекулы определяется числом электронных пар валентной оболочки (ЭПВО), в которые не включают электронные пары, образующие p-связи.
2. Электронные пары валентной оболочки ориентируются так, чтобы отталкивание между ними было минимально.
3. Неподеленные электронные пары занимают больший объем околоядерного пространства, чем связывающие. Следствием неэквивалентности неподеленных и связывающих электронных пар является искажение валентных углов.
Чтобы определить число ЭПВО необходимо сложить число валентных электронов данного атома с числом электронов, предоставленных присоединенными атомами, а затем из полученной суммы вычесть число электронов, образующих p-связи, и разделить полученный результат на два. Так, для молекулы СО2, имеющей две s- и две p-связи, каждый атом кислорода предоставляет по два электрона на образование связей с атомом углерода, а атом углерода предоставляет по два электрона на образование связей с каждым атомом кислорода. Соответственно число ЭПВО для атома углерода равно 2:

Число связывающих ЭПВО равно числу s-связей, образуемых центральным атомом (Ns); разность равна числу неподеленных электронных пар: Nнп = NЭПВО - Ns.
Идеальные геометрические формы, отвечающие различным значениям числа ЭПВО и неподеленных электронных пар, приведены в табл. 6, в скобках указан атом, для которого определяется тип гибридизации.
Если валентная оболочка атома в молекуле включает две электронные пары, два одноименных точечных заряда, оказавшись на поверхности сферы, расположатся на концах диаметра большого круга. Соответственно две ЭПВО должны занять орбитали, обеспечивающие валентный угол 180°, что согласно методу валентных связей отвечает sp-гибридизации атомных орбиталей. Максимальному удалению и минимальному отталкиванию трех ЭПВО будет отвечать ориентация орбиталей от центра к вершинам равностороннего треугольника (sp2-гибридизация). Четырем ЭПВО соответствует тетраэдрическая конфигурация (sp3-гибридизация). В случае пяти ЭПВО наиболее выгодным является распределение электронных пар по направлениям к вершинам тригональной бипирамиды (sp3d-гибридизация), шести ЭПВО соответствует октаэдрическая конфигурация (sp3d2-гибридизация).
При наличии неподеленных электронных пар геометрия молекулы изменяется в зависимости от их числа. Как видно из табл. 6, в случае трех ЭПВО молекулы могут быть угловыми (Nнп = 1) и линейными (Nнп =2). Наличие в валентной оболочке четырех электронных пар допускает образование тригонально-пирамидальных при Nнп = 1, угловых при Nнп = 2 и линейных (Nнп = 3) молекул.
Если число ЭПВО равно пяти и все пары являются связывающими, молекула имеет форму тригональной бипирамиды. При наличии неподеленных электронных пар необходимо знать, какие орбитали, аксиальные или экваториальные, будут заняты ими. Расчет показывает, что более выгодным является экваториальное положение. Действительно, занимающие экваториальное положение неподеленные пары имеют только двух ближайших соседей под углом 90 °, тогда как при аксиальном положении таких соседей было бы три, что привело бы к более сильному отталкиванию. В результате молекула с одной неподеленной парой имеет форму бисфеноида (искаженный тетраэдр), с двумя - Т-форму, а трем неподеленным парам соответствуют линейные молекулы.
Таблица 6.
Геометрия молекул s- и p-элементов
| NЭПВО
| Тип
гибридизации
| Число неподеленных пар
|
|
|
|
|
|
|
| sp
|  линейная
BeF2 (Be)
линейная
BeF2 (Be)
|  линейная
AlF (Al)
линейная
AlF (Al)
|
|
|
|
| sp2
|
 треугольник
BF3 (B)
треугольник
BF3 (B)
|
 угловая
SnCl2 (Sn)
угловая
SnCl2 (Sn)
|
 линейная
NH (N)
линейная
NH (N)
|
|
|
| sp3
|
 тетраэдр
CF4 (C)
тетраэдр
CF4 (C)
|
 тригональная пирамида
NH3 (N)
тригональная пирамида
NH3 (N)
|
 угловая
Н2О (О)
угловая
Н2О (О)
|
 линейная
IF (I)
линейная
IF (I)
|
|
| sp3d
|
 тригональная бипирамида
PF5 (P)
тригональная бипирамида
PF5 (P)
|
 бисфеноид
SF4 (S)
бисфеноид
SF4 (S)
|
 T-форма
IF3 (I)
T-форма
IF3 (I)
|
 Линейная
XeF2 (Xe)
Линейная
XeF2 (Xe)
|
|
| sp3d2
|
 октаэдр
SF6 (S)
октаэдр
SF6 (S)
|
 тетрагональная пирамида
BrI5 (Br)
тетрагональная пирамида
BrI5 (Br)
|
 квадрат
XeF4 (Xe)
квадрат
XeF4 (Xe)
|
 Т-форма
[XeF3]- (Xe)
Т-форма
[XeF3]- (Xe)
|
В случае шести ЭПВО неподеленные пары занимают в октаэдре транс-положение друг относительно друга. В силу этого для шести ЭПВО реализуются следующие формы молекул: октаэдр (Nнп = 0), тетрагональная пирамида (Nнп = 1), квадрат (Nнп = 2) и т.д..
Чтобы определить геометрическую форму молекулы по методу Гиллеспи, необходимо знать электронные конфигурации атомов, порядок соединения этих атомов в молекуле, число s- и p-связей в образовавшейся частице и учесть эффекты, приводящие к искажению валентных углов.. Рассмотрим несколько примеров.
Пример 1. Для молекулы COCl2, в которой атом кислорода образует с углеродом двойную связь, а атомы хлора – одинарные (рис. 20а), числа ЭПВО и неподеленных пар составляют:
NЭПВО(C) =  ; Nнп(С) = 3 - 3 = 0
; Nнп(С) = 3 - 3 = 0
Поэтому молекула COCl2 должна иметь форму равностороннего треугольника с валентными углами, равными 120°. В действительности же эта молекула имеет форму равнобедренного треугольника (dC=O = 117 пм, dC-Cl = 175 пм, ÐClCO = 124 °, ÐСlCCl = 111 °). Поскольку кратные связи занимают больший объем у центрального атома, что приводит к сжатию валентных углов.
Пример 2. Для молекулы CHCl3 число ЭПВО и связывающих пар одинаково (NЭПВО = 4, Nнп = 0), однако молекула хлороформа не имеет форму правильного тетраэдра (dC-Cl =176 пм, dC-H = 110 пм, ÐClCCl = 111,3 °, ÐHCCl = 107,5°). Это связано с неравноценностью присоединенных атомов: атом водорода и атомы хлора имеют различные радиусы и образуют различные по длине связи с атомом углерода.
Пример 3. Определим форму молекулы оксофторида ксенона XeO2F2, в которой центральным является атом ксенона, образующий четыре s- и две p-связи (рис. 20б).
Числа ЭПВО и неподеленных пар валентной оболочки хсенона составляют:
NЭПВО(Xe) = 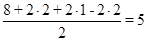 ; Nнп(Xe) = 5 - 4 = 1
; Nнп(Xe) = 5 - 4 = 1
В соответствии с табл. 10 образующаяся молекула имеет форму бисфеноида, в котором атомы кислорода образуют связи за счет экваториальных орбиталей, обеспечивающих этим атомам максимальное удаление от орбитали, занятой неподеленной парой, а атомы фтора, имеющие по три неподеленные пары, находятся в транс-положении. Можно ожидать, что длина двойных связей Xe=O будет меньше длины одинарных связей Xe-F, а углы OXeO и FXeF в связи с наличием неподеленной пары на экваториальной орбитали будут меньше 120 ° и 180 ° соответственно. Эти предположения хорошо согласуются с результатами экспериментального определения формы рассматриваемой частицы: молекула XeO2F2 действительно имеет форму слегка искаженного бисфеноида (dXe=O = 171 пм, dXe-F = 190 пм, ÐOXeO = 105,7 °, ÐFXeF = 174,7°).
Пример 4. Определим геометрию газообразного метабората натрия (рис. 20в).
При определении геометрии сложных молекул, содержащих цепочки из четырех и более атомов, рационально разбить молекулу на фрагменты и определить геометрию каждого из них отдельно. Для метабората натрия следует порознь определить форму фрагментов O=B-O и B-O-Na. Для атома бора:
NЭПВО(В) =  Nнп(В) = 2 - 2 = 0;
Nнп(В) = 2 - 2 = 0;
т.е. фрагмент O=B-O имеет линейную форму.
NЭПВО(О) =  Nнп(O) = 4 - 2 = 2
Nнп(O) = 4 - 2 = 2
Таким образом, фрагмент B-O-Na имеет угловую форму, валентный угол близок к 109,5 °. Молекула NaBO2 действительно представляет собой сочетание линейного и углового фрагментов с валентными углами 180 ° и 109 ° (рис. 20в).

Рис. 20. Структурные формулы молекул СOCl2 (а), XeOF2 (б), NaBO2 (в).
Пример 5. Определим геометрию иона IO2F2-.
Если частица является ионом, то при расчете числа ЭПВО следует вычесть заряд иона из числа валентных электронов. Для атома иода, являющегося центральным и образующего четыре s- и две p-связи:
NЭПВО(I) =  Nнп(I) = 5 - 4 = 1
Nнп(I) = 5 - 4 = 1
Рассматриваемый ион должен иметь форму бисфеноида, что подтверждено экспериментально.






 линейная
BeF2 (Be)
линейная
BeF2 (Be)
 линейная
AlF (Al)
линейная
AlF (Al)
 треугольник
BF3 (B)
треугольник
BF3 (B)
 угловая
SnCl2 (Sn)
угловая
SnCl2 (Sn)
 линейная
NH (N)
линейная
NH (N)
 тетраэдр
CF4 (C)
тетраэдр
CF4 (C)
 тригональная пирамида
NH3 (N)
тригональная пирамида
NH3 (N)
 угловая
Н2О (О)
угловая
Н2О (О)
 линейная
IF (I)
линейная
IF (I)
 тригональная бипирамида
PF5 (P)
тригональная бипирамида
PF5 (P)
 бисфеноид
SF4 (S)
бисфеноид
SF4 (S)
 T-форма
IF3 (I)
T-форма
IF3 (I)
 Линейная
XeF2 (Xe)
Линейная
XeF2 (Xe)
 октаэдр
SF6 (S)
октаэдр
SF6 (S)
 тетрагональная пирамида
BrI5 (Br)
тетрагональная пирамида
BrI5 (Br)
 квадрат
XeF4 (Xe)
квадрат
XeF4 (Xe)
 Т-форма
[XeF3]- (Xe)
Т-форма
[XeF3]- (Xe)
 ; Nнп(С) = 3 - 3 = 0
; Nнп(С) = 3 - 3 = 0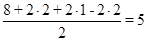 ; Nнп(Xe) = 5 - 4 = 1
; Nнп(Xe) = 5 - 4 = 1 Nнп(В) = 2 - 2 = 0;
Nнп(В) = 2 - 2 = 0; Nнп(O) = 4 - 2 = 2
Nнп(O) = 4 - 2 = 2
 Nнп(I) = 5 - 4 = 1
Nнп(I) = 5 - 4 = 1


