В связи с высокой сложностью взаимодействия в системах растворитель - растворенное вещество общую теорию растворов до сих пор не удалось создать. Наиболее простые закономерности должны быть присущи идеальному раствору, для которого ΔНраств и ΔVраств равны нулю, а химическое взаимодействие компонентов отсутствует. Из реальных растворов к идеальному раствору приближаются разбавленные растворы неэлектролитов. Изучение этой группы растворов показало, что некоторые свойства их не зависят от природы растворенного вещества, а определяются лишь концентрацией раствора и природой растворителя. Подобные свойства получили название коллигативных свойств растворов. К коллигативным свойствам относятся давление насыщенного пара над раствором, температуры кипения и замерзания раствора, а также осмотическое давление раствора.
Давление насыщенного пара над раствором. Для веществ, способных переходить без разложения в газообразное состояние, одним из важных физических свойств является давление насыщенного пара. Пусть вещество в твердом или жидком состоянии, находясь в замкнутом сосуде, контактирует с газовой фазой. В этом случае на поверхности раздела фаз будут протекать процессы испарения (сублимации) и конденсации (десублимации). Спустя некоторое время такая система придет в состояние равновесия при определенном давлении пара, обеспечивающем равенство скоростей прямого и обратного процессов. Таким образом, при постоянной температуре давление насыщенного пара для данного вещества постоянно. Поскольку процесс испарения эндотермичен, повышение температуры будет сопровождаться повышением давления насыщенного пара. Диаграммы, выражающие зависимость между температурой и давлением насыщенного пара, называются диаграммами состояния вещества. На рис. 23 представлена диаграмма состояния вещества, существующего в кристаллическом, жидком и газообразном состояниях, построенная в координатах "температура – давление".
Диаграмма состоит из трех полей. Поле АОВ включает множество значений р и Т, отвечающих газообразному состоянию вещества. Поля ВОD и AOD отвечают условиям, при которых вещество находится в жидком (поле ВОD) или твердом (поле AOD) состоянии. Линии, разграничивающие указанные поля, соответствуют значениям р и Т, при которых система двухфазна. Линия АО отвечает условиям, при которых в состоянии равновесия находятся твердое вещество и его пар, кривая ОВ - жидкость и пар, кривая OD - твердое вещество и жидкость. Точка О соответствует температуре и давлению, при которых в состоянии равновесия находятся пар, жидкость и кристаллы данного вещества (тройная точка). Так, для воды тройная точка отвечает температуре 273,15 К и давлению водяного пара, равному 610 Па.
При изменении температуры и давления число фаз системы может изменяться. Число параметров, которые можно изменять независимо друг от друга без изменения числа фаз, называют числом степеней свободы. Последнее связано с числом компонентов и фаз системы правилом фаз Гиббса:
С + Ф = К + 2,
где С - число степеней свободы, Ф - число фаз, К - число компонентов.

Рис. 23. Диаграмма состояния для растворителя и раствора.
Если система однокомпонентна, С = 3 – Ф. Правило фаз позволяет определить число степеней свободы в любой точке диаграммы состояния. Так, для точки R (рис. 23) К = 1, Ф = 1, откуда С = 2. Действительно, для этого состояния температуру и давление можно в определенных пределах менять независимо друг от друга, а система будет оставаться однофазной (например, при переходе из точки R в точку R1). Для точки U K = 1, Ф = 2, С = 1, т.е. можно произвольно изменять лишь один параметр (либо р, либо Т), а второй параметр должен изменяться строго определенным образом, чтобы точка U1 осталась на линии ОВ. Наконец, для тройной точки О число степеней свободы равно нулю; в этом случае изменение хотя бы одного параметра приводит к превращению трехфазной системы в двухфазную или однофазную.
Пусть в чистый растворитель вводят растворимое в нем нелетучее соединение. В результате концентрация этого вещества в растворе возрастает от нуля до некоторой величины, а концентрация растворителя уменьшается. В соответствии с принципом Ле Шателье равновесие
испарение
раствор  пар
пар
конденсация
должно сместиться в сторону процесса, сопровождающегося понижением концентрации растворенного вещества и повышением концентрации растворителя, т.е. процесса конденсации. Давление насыщенного пара при этом уменьшится. Отсюда следует, что давление пара над раствором ниже давления пара над чистым растворителем. Соответственно на диаграмме состояния линия давления насыщенного пара над раствором О'В' пройдет ниже кривой ОВ.
Взаимосвязь между давлением насыщенного пара и концентрацией раствора отражает первый закон Рауля (1887 г.). Относительное понижение давления насыщенного пара над раствором равно мольной доле растворенного вещества:
 ,
,
где р0 и р1 - давление насыщенного пара над растворителем и раствором, ν0 и ν1 - количества (число молей) растворителя и растворенного вещества. Преобразование уравнения приводит к формуле следующего вида:
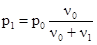
Таким образом, давление пара над раствором равно давлению пара над чистым растворителем, умноженным на мольную долю растворителя.
Температуры замерзания и кипения растворов. Вещество характеризуется определенными температурами кипения и замерзания (кристаллизации). Эти характеристики непосредственно связаны с давлением его насыщенного пара.
Температура кипения жидкости - это температура, при которой давление насыщенного пара над жидкостью становится равным внешнему давлению. При этой температуре переход жидкости в пар происходит не только с поверхности жидкости, но и во всем ее объеме, вследствие чего в жидкой фазе наблюдается непрерывное образование и рост пузырьков пара, всплывающих и разрушающихся. На диаграмме состояния (рис. 23) кипению жидкости соответствует температура Тoкип, при которой давление пара над жидкостью (кривая ОВ) становится равным внешнему давлению рвнеш. При постоянном давлении температура кипения зависит от природы жидкости. Так, при стандартном давлении вода кипит при 100 оС, бензол - при 80,1 оС, этанол - при 78,4 оС.
Поскольку давление насыщенного пара над раствором меньше, чем над растворителем, растворы кипят при более высоких температурах, чем чистый растворитель. Так, при температуре Тoкип давление пара над раствором (отрезок GF) будет меньше внешнего давления (отрезок EF), и раствор кипеть не будет. Чтобы раствор закипел, его необходимо нагреть до температуры Т'кип, при которой давление насыщенного пара достигнет внешнего давления.
Температурой замерзания жидкого вещества является температура, при которой твердая и жидкая фазы находятся в состоянии равновесия. Необходимым условием равновесия между жидкой и твердой фазой является равенство значений давления насыщенного пара над жидкостью (рж) и над твердым веществом (рк). Если условие рк = рж не соблюдается, то фаза с большим давлением пара переходит в фазу с меньшим давлением пара.
Так, на рис. 23 равновесие между твердой и жидкой фазами растворителя наблюдается при температуре Тoзам. Пусть в раствор, охлажденный до температуры замерзания чистого растворителя Тoзам, поместили кристалл твердого растворителя. В такой системе давление насыщенного пара над твердой фазой (отрезок OМ) будет больше давления пара над раствором (отрезок SМ), и твердый растворитель перейдет в жидкое состояние. Для того чтобы между раствором и кристаллами твердого растворителя установилось равновесие, систему необходимо охладить до температуры Т'зам, при которой давление пара над раствором и кристаллическим растворителем станут одинаковыми (отрезок O'K). Таким образом, растворы замерзают при более низких температурах, чем чистый растворитель. Ф. Рауль, изучая влияние концентрации раствора и природы растворителя на замерзание и кипение растворов, установил закономерность, называемую вторым законом Рауля. Повышение температуры кипения и понижение температуры замерзания раствора по отношению к чистому растворителю пропорционально числу частиц растворенного вещества в единице массы растворителя и не зависит от природы растворенного вещества.
Математически второй закон Рауля выражается следующими уравнениями:
ΔТкип = ECm, ΔТзам = КСm,
где ΔТкип и ΔТзам - повышение температуры кипения и понижение температуры замерзания раствора, Сm - моляльная концентрация раствора, Е (эбулиоскопическая константа) и К (криоскопическая константа) - коэффициенты пропорциональности, зависящие от природы растворителя. Так, для воды эбулиоскопическая и криоскопическая константы равны соответственно 0,516 и 1,86, а для бензола - 2,57 и 5,12.
На втором законе Рауля основаны эбулиоскопический и криоскопический методы определения молекулярных масс растворенных веществ. Подставив в уравнения выражение для значение Сm и решив их относительно М1, получим:
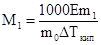 ;
; 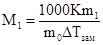 ,
,
где m1 и М1 - масса и молекулярная масса растворенного вещества, m0 - масса растворителя.
Осмос и осмотическое давление. Если привести в соприкосновение раствор и растворитель или два раствора с различными концентрациями, то в системе начнет протекать процесс диффузии, приводящий к выравниванию концентраций этих растворов. Процесс диффузии протекает самопроизвольно, так как он сопровождается возрастанием энтропии системы, и носит двухсторонний характер: выравнивание концентраций достигается за счет диффузии молекул растворенного вещества и растворителя.
Иначе протекает процесс выравнивания концентраций, если растворитель и раствор отделить друг от друга мембраной, проницаемой для молекул растворителя, но непроницаемой для молекул растворенного вещества (полупроницаемая мембрана). Схема подобного эксперимента приведена на рис. 24. В сосуд 1 с чистым растворителем погружен заполненный раствором сосуд 2, дно которого является полупроницаемой мембраной (3). В такой системе уменьшение разности концентраций в сосудах может осуществляться только за счет проникновения растворителя из сосуда 1 в сосуд 2. Объем раствора в сосуде 2 при этом увеличивается, и уровень жидкости в градуированной трубке 4 поднимается.
Самопроизвольный переход растворителя через полупроницаемую мембрану, разделяющую раствор и растворитель или два раствора с различной концентрацией называется осмосом.
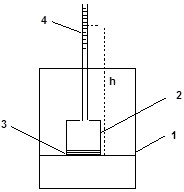
Рис. 24. Осмометр: 1 – сосуд с растворителем; 2 – сосуд с раствором;
3 – полупроницаемая мембрана; 4 – градуированная трубка.
Осмос можно рассматривать как одностороннюю диффузию растворителя через полупроницаемую мембрану. В качестве полупроницаемых мембран используют пленки из природных и синтетических полимеров (оболочка мочевого пузыря животных, пленки из нитроцеллюлозы и т.д.). Очень прочные полупроницаемые перегородки получают из пористого фарфора, обработанного последовательно растворами CuSO4 и K4[Fe(CN)6]; в порах фарфора при этом осаждается гексацианоферрат меди Cu2[Fe(CN)6], придающий материалу свойство полупроницаемости.
Столб жидкости в трубке 4 оказывает на раствор в сосуде 2 внешнее (гидростатическое) давление, противодействующее осмосу. Под действием внешнего давления растворитель просачивается через мембрану из сосуда 2 в сосуд 1 (обратный осмос). При определенной высоте столба жидкости h в системе устанавливается динамическое равновесие, после чего объем раствора перестает изменяться.
Мера стремления системы «растворитель - полупроницаемая мембрана – раствор» к равномерному распределению растворенного вещества называется осмотическим давлением раствора. Осмотическое давление равно внешнему давлению, которое необходимо приложить к раствору, чтобы привести его в равновесие с чистым растворителем, отделенным от раствора полупроницаемой мембраной.
В середине XIX столетия было установлено, что осмотическое давление растворов прямо пропорционально абсолютной температуре и обратно пропорционально разбавлению раствора. Г. Вант-Гофф обратил внимание на аналогию этих закономерностей с газовыми законами Гей-Люссака и Бойля-Мариотта и сформулировал в 1887 году закон, позволяющий теоретически рассчитывать осмотическое давление. Осмотическое давление раствора равно давлению, которое оказывало бы растворенное вещество, находящееся в газообразном состоянии и занимающее объем, равный объему раствора.
В соответствии с законом Вант-Гоффа для расчета осмотического давления можно использовать уравнение состояния идеального газа, которое применительно к осмотическому давлению примет вид:
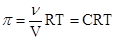 ,
,
где p - осмотическое давление в Па, С - концентрация растворенного вещества в моль/м3. Если концентрацию выражать в моль/л, то уравнение приобретет следующий вид:

Растворы электролитов






 пар
пар ,
,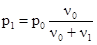
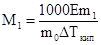 ;
; 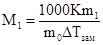 ,
,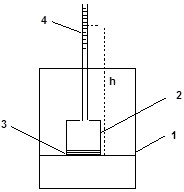
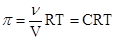 ,
,

